-
 RussellA
2.6kHowever, I'm not sure about the left drawing. It doesn't show that mammals are a subset of animals. It shows that only a part of mammals are also animals. — Alkis Piskas
RussellA
2.6kHowever, I'm not sure about the left drawing. It doesn't show that mammals are a subset of animals. It shows that only a part of mammals are also animals. — Alkis Piskas
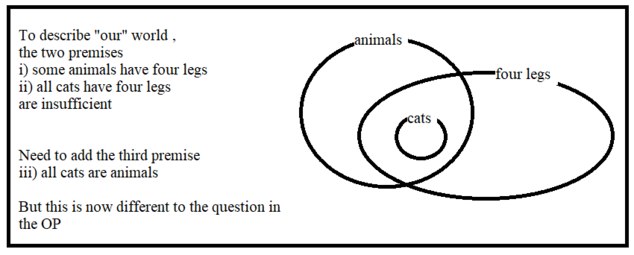
I agree that the left hand drawing is not correct for "our" world, where i) all mammals are animals (all B's are A's) ii) all cats are mammals (all C's are B's)
But the OP is not asking a question about "our" world. The OP is asking a question about a "possible" world, perhaps a fictional world, where i) some animals are mammals (some A's are B's) ii) all cats are mammals (all C's are B's), in which case the left hand drawing is correct. -
 Alkis Piskas
2.1k
Alkis Piskas
2.1k
Certainly. But I have edited my reply and gave you right after I checked the label "possible world" ... Also, I presented a more interesting and realistic scheme ...
See the update at https://thephilosophyforum.com/discussion/comment/646385 -
 RussellA
2.6k
RussellA
2.6k -
 Alkis Piskas
2.1k
Alkis Piskas
2.1k
In what the OP said, I have replaced "Ayes" with "animals", "Bees" with "four legs" and "Seas" with "cats". All the rest is the same. The conclusion (D or E) is what the OP also thought (maybe for another reason though). -
 TonesInDeepFreeze
3.8kIf you have a dollar in your pants pocket, do you (not) have also 32 cents?
TonesInDeepFreeze
3.8kIf you have a dollar in your pants pocket, do you (not) have also 32 cents?
— tim wood
No, you don't. A dollar is a dollar and cents are cents. Also, you cannot use some vending, gambling etc. machines if you don't have the exact amount of cents. — Alkis Piskas
That is ridiculous captiousness. The example is not vitiated by quibbles about the difference between coins and bills. The point of the example is that you can have Some and also All.
Again, I pointed out to you that in the context of basic logic, 'some' means 'at least one' and doesn't mean 'some but not all'.
it is true because its inference is valid — Alkis Piskas
To be clear, a valid inference does not ensure the truth of the conclusion. A valid inference does ensure the truth of the conclusion when either (1) the premises are true or (2) the conclusion is logically true anyway.
A) Some animals are cats: True, since mammals are animals (based on the first premise) and cats are mammals
— Alkis Piskas
You can infer this adding additional information, but you cannot from the premises given validly conclude it.
— tim wood
You are right that you have to infer it, i.e. we don't know that directly, but it is true because its inference is valid, — Alkis Piskas
No, your inference is not valid. It is true that some animals are cats, but it does not follow from your premises.
Mammals are a subset of animals. Cats are a subset of mammals. That is, cats are a subset of a subset of animals. — Alkis Piskas
Yes, that is valid. But that is different from your original argument.
It is true that some animals are cats. But it is not entailed by your premises.
— TonesInDeepFreeze
If it is true, well, it is True! That's what I said! — Alkis Piskas
No, what you said is that it follows from your premises.
Saying that "some cats are mammals" suggests that there are some cats that are not mammals. — Alkis Piskas
In certain everyday contexts, yes, 'some' may mean or at least suggest 'not all'. But not in the study of basic logic. I'll say it again: In ordinary basic logic [also, in certain other everyday contexts]
'some' means 'at least one' and it doesn't mean 'some but not all'.
(A) is true, but it is not entailed by your premises.
— TonesInDeepFreeze
Yes, you have already said that! — Alkis Piskas
Yet you made the same mistake in a subsequent post!
B) Some cats have four legs: False, since we know that "All cats have four legs" (and not only some) — Alkis Piskas
Wrong. For the fourth time, I'm telling you that in basic logic 'some' means 'at least one' and not 'some but not all'.
"No animals" is ambiguous — Alkis Piskas
I pointed out before that that is wrong. You merely persist in claiming again what has already been explained to you to be incorrect. -
 TonesInDeepFreeze
3.8kIn basic logic:
TonesInDeepFreeze
3.8kIn basic logic:
"Some cats are mammals"
means
"There is a thing that is both a cat and a mammal"
"All cats are mammals"
means
"If a thing is a cat then it is a mammal"
"No cats are mammals"
means
"If a thing is a cat then it is not a mammal"
means
"All cats are not mammals"
"Some cats are not mammals"
means
"There is a thing that is a cat and is not a mammal"
There is no ambiguity.
/
Moreover:
"Some cats are mammals" does NOT imply "Some cats are not mammals".
"All cats are mammals" does NOT imply 'Some cats are mammals" (because, if there are no cats, then "All cats are mammals" is vacuously true but "Some cats are mammals" is false). (Though I don't recall what, if anything, Aristotle said about that; and, while the notion of vacuous truth is basic in usual formal logic, it is not ordinarily used in everyday logic.) -
 TonesInDeepFreeze
3.8kEquivalences:
TonesInDeepFreeze
3.8kEquivalences:
"It is not the case that some cats are mammals"
is equivalent to
'No cats are mammals"
"It is not the case that all cats are mammals"
is equivalent to
"Some cats are not mammals"
"It is not the case that no cats are animals"
is equivalent to
"Some cats are mammals"
"It is not the case that some cats are not mammals"
is equivalent to
"All cats are mammals" -
 TonesInDeepFreeze
3.8kThis goes to the existential problem — tim wood
TonesInDeepFreeze
3.8kThis goes to the existential problem — tim wood
Yes,that matter hinges on existential import. But the problem in the first post of this thread does not. Nor does your other concern about undistributed middle.
"The presupposition [...] contradictory relation." — tim wood
All of that quote seems correct to me and it in no way vitiates anything I've said, and it in no way supports your notion that the question of this thread hinges on existential import or undistributed middle.
house rules — tim wood
Of course, discussions about drawing inferences need to be in context of what principles of logic we have in mind. But the question in this thread has been answered according to everyday principles of reasoning, which also are formalized. And those particular principles do not hinge in any way on matters of existence or vacuity. I have explained exactly why that is in this case. I don't know why you continue to ignore it.
You mentioned cutting a knot with a knife. I rebutted that analogy already. But with your fixation that existential import plays a role in the particular question of this thread, you remind me of the saying that if a person has only a hammer then everything looks like a nail. -
 TonesInDeepFreeze
3.8k
TonesInDeepFreeze
3.8k
Because you never said you gave it up; and your next post seemed to still be trying to connect existential import to what we had been discussing. Granted, it is also reasonable that you were not trying to make the earlier connection, in which case I would grant my previous post would have been beating a dead horse. -
 John McMannis
78I say A. If some ayes are bees, and seas are bees, then some ayes are sees. Unless not all bees are sees, which isn't given.
John McMannis
78I say A. If some ayes are bees, and seas are bees, then some ayes are sees. Unless not all bees are sees, which isn't given. -
 TonesInDeepFreeze
3.8kIf some ayes are bees, and seas are bees, then some ayes are sees. Unless not all bees are sees, which isn't given. — John McMannis
TonesInDeepFreeze
3.8kIf some ayes are bees, and seas are bees, then some ayes are sees. Unless not all bees are sees, which isn't given. — John McMannis
Yes, "Not all Beas are Seas" is not a premise. But "All Beas are Seas" is also not a premise. So you don't get to use either in the inference.
An inference is not valid when there is an example in which the premises are true and the conclusion is false. Here's an example.
Let the set of Ayes be {Jack}
Let the set of Beas be {Jack, Lucy}
Let the set of Seas be {Lucy}
So:
"Some Ayes are Bees" True
"All Seas are Bees" True
"Some Ayes are Seas" False
So the inference is invalid. -
 RussellA
2.6kIn what the OP said, I have replaced "Ayes" with "animals", "Bees" with "four legs" and "Seas" with "cats". All the rest is the same. The conclusion (D or E) is what the OP also thought (maybe for another reason though). — Alkis Piskas
RussellA
2.6kIn what the OP said, I have replaced "Ayes" with "animals", "Bees" with "four legs" and "Seas" with "cats". All the rest is the same. The conclusion (D or E) is what the OP also thought (maybe for another reason though). — Alkis Piskas
I have redrawn my Venn Diagram, including @Raymond and @tim wood's suggestions, and using animals, etc rather than Ayes, etc. The solution is still D.
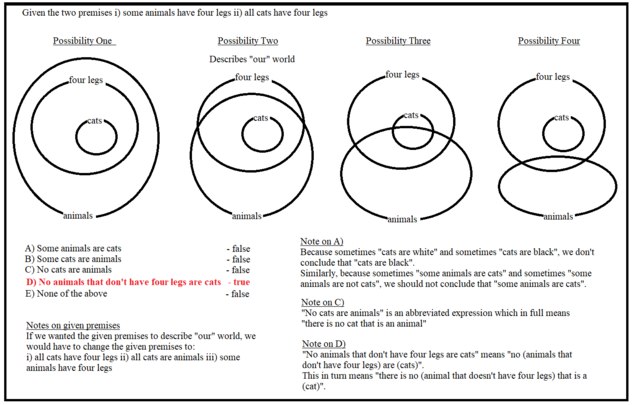
-
 Agent Smith
9.5kI believe there's no need to rack our brains on such a simple matter.
Agent Smith
9.5kI believe there's no need to rack our brains on such a simple matter.
1. Some Ayes are Bees.
2. All Seas are Bees.
No conclusion follows.
1. Some colors are white.
2. All snow are white.
Ergo,
??? -
 TonesInDeepFreeze
3.8kthere's no need to rack our brains on such a simple matter. — Agent Smith
TonesInDeepFreeze
3.8kthere's no need to rack our brains on such a simple matter. — Agent Smith
Yes, it is a simple matter that (D) is the correct answer.
1. Some Ayes are Bees.
2. All Seas are Bees.
No conclusion follows. — Agent Smith
No, many conclusions follow. And one of them is:
No Ayes that are not Bees are Seas.
Moreover, it follows from "All Seas are Beas" alone.
And one shouldn't have to rack one's brain to see that, except you still haven't racked your brain enough. -
 jgill
4k
jgill
4k -
 TonesInDeepFreeze
3.8k:roll: — jgill
TonesInDeepFreeze
3.8k:roll: — jgill
I don't know what to make of people who still can't see it after it's been explained six ways to Sunday. -
 Agent Smith
9.5k:up: Good that you cleared that up for me.
Agent Smith
9.5k:up: Good that you cleared that up for me.
In my defense though, I wasn't looking at immediate inferences like you are; rather I was trying to see if the two statements could be used to form a classic syllogism; they can't! -
 TonesInDeepFreeze
3.8kI was trying to see if the two statements could be used to form a classic syllogism — Agent Smith
TonesInDeepFreeze
3.8kI was trying to see if the two statements could be used to form a classic syllogism — Agent Smith
Yes, we went through that with tim wood. Anyway, glad that you see now that (D) is the answer. -
 TonesInDeepFreeze
3.8k
TonesInDeepFreeze
3.8k
Try it this way:
Some Americans are Brainy.
All Statisticians are Brainy.
We want to prove:
No American that is not Brainy is a Statistician.
But "No American that is not Brainy is a Statistician" means the same as "If something is an American and not Brainy, then it is not a Statistician."
Now, since, all Statisticians are Brainy, it follows that if something is not Brainy then it is not a Statistician. So, perforce, if something is an American and not Brainy, then it is not a Statistician. QED.
But what about the premise "Some Americans are Brainy"? Well, we never used it. We didn't need to. Which is fine. If a statement (such as "All Statisticians are Brainy") proves a conclusion, then that statement plus any other extra unneeded statement (such as "Some Americans are Brainy") still proves the conclusion (this is the principle of Monotonicity of Entailment). -
 jgill
4k
jgill
4k -
 TonesInDeepFreeze
3.8kIt's simply impossible! — Agent Smith
TonesInDeepFreeze
3.8kIt's simply impossible! — Agent Smith
It's impossible for you to understand?
What is the first sentence in my previous post that you don't understand?
Welcome to The Philosophy Forum!
Get involved in philosophical discussions about knowledge, truth, language, consciousness, science, politics, religion, logic and mathematics, art, history, and lots more. No ads, no clutter, and very little agreement — just fascinating conversations.
Categories
- Guest category
- Phil. Writing Challenge - June 2025
- The Lounge
- General Philosophy
- Metaphysics & Epistemology
- Philosophy of Mind
- Ethics
- Political Philosophy
- Philosophy of Art
- Logic & Philosophy of Mathematics
- Philosophy of Religion
- Philosophy of Science
- Philosophy of Language
- Interesting Stuff
- Politics and Current Affairs
- Humanities and Social Sciences
- Science and Technology
- Non-English Discussion
- German Discussion
- Spanish Discussion
- Learning Centre
- Resources
- Books and Papers
- Reading groups
- Questions
- Guest Speakers
- David Pearce
- Massimo Pigliucci
- Debates
- Debate Proposals
- Debate Discussion
- Feedback
- Article submissions
- About TPF
- Help
More Discussions
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum