-
 TonesInDeepFreeze
3.8kDon't need a logic professor.
TonesInDeepFreeze
3.8kDon't need a logic professor.
If x is a C, then x is a B.
Therefore, if x is not a B, then x is not a C.
So, perforce, if x is both an A and not a B, then x is not a C.
That argument involves no assumptions about whether or not there is a something that is an A, B, or C. -
 TonesInDeepFreeze
3.8kElse we willy-nilly prove the existence of God, Zeus, unicorns, and the two-horned rhinoceros sleeping in my bed. — tim wood
TonesInDeepFreeze
3.8kElse we willy-nilly prove the existence of God, Zeus, unicorns, and the two-horned rhinoceros sleeping in my bed. — tim wood
This argument does not prove the existence of anything.
it asks for a conclusion, not an inference — tim wood
The problem was not what conclusion is true, but rather what conclusion can be drawn from the premises. That is inference.
If, for example, there were As that at the same time are not Bs, then D follows. But that hypothetical is not given. — tim wood
(D) follows from the premises (actually, only one of the premises is needed) no matter what does or does not exists.
I spelled out the logic of the argument explicitly. There is no existence assumption in the argument. Moreover, A's are irrelevant to the argument. -
 TonesInDeepFreeze
3.8kYou get your D, but only on expanding the terms of the problem. — tim wood
TonesInDeepFreeze
3.8kYou get your D, but only on expanding the terms of the problem. — tim wood
False. I expanded nothing. I made no assumption other than the premise "All Seas are Beas".
"All Seas are Beas" implies "All non-Beas are non-Seas" implies, perforce, "All things that are both non-Ayes and non-Beas are non-Seas".
And that argument holds whether or not there are Ayes or Beas or Seas.
There is no existence premise nor existence conclusion involved.
/
It is alarming that someone would fail to understand the correctness of the inference, irrespective of training in logic, but rather just as a matter of commonly acquired reasoning. -
 TonesInDeepFreeze
3.8konly in outdated, Aristotelian categories it's "E" — DavidJohnson
TonesInDeepFreeze
3.8konly in outdated, Aristotelian categories it's "E" — DavidJohnson
Because Aristotelian syllogisms do not exhaust even very basic reasoning. -
 TonesInDeepFreeze
3.8kAristotelian logic, on the other hand, may be not so useful in some modern applications, but it is not wrong. — tim wood
TonesInDeepFreeze
3.8kAristotelian logic, on the other hand, may be not so useful in some modern applications, but it is not wrong. — tim wood
It's not wrong. It's just that it is nowhere close to covering much of everyday deductive reasoning. -
 TonesInDeepFreeze
3.8kwhat, if any, house rules may be in effect. — tim wood
TonesInDeepFreeze
3.8kwhat, if any, house rules may be in effect. — tim wood
The house rules are everyday common reasoning. -
 Raymond
815All Seas are Beas" implies "All non-Beas are non-Seas" — TonesInDeepFreeze
Raymond
815All Seas are Beas" implies "All non-Beas are non-Seas" — TonesInDeepFreeze
What if all Seas are real numbers and Beas are complex ñumbers? Are all non-complex numbers non real numbers then? -
 RussellA
2.6kmore examples — Josh Alfred
RussellA
2.6kmore examples — Josh Alfred
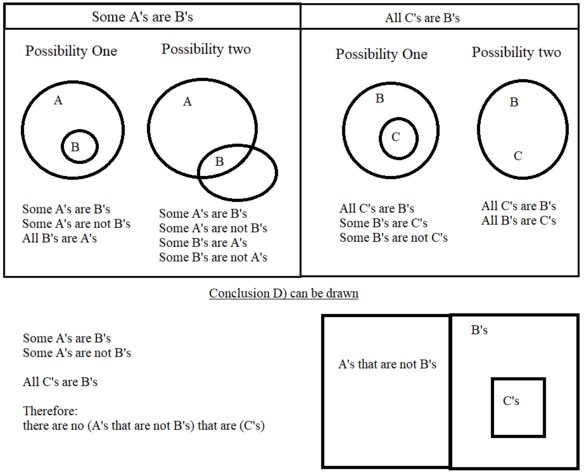
I am afraid the image is not from an "authoritative" source.
I used Microsoft "Paint".
For a few dollars a year one can subscribe to the Forum and be able to upload images onto the Forum - well worth the money. -
 RussellA
2.6kwould D still be a valid conclusion — DavidJohnson
RussellA
2.6kwould D still be a valid conclusion — DavidJohnson
@TonesInDeepFreeze gets to the heart of the matter. Personally, trying to solve in words would make my head explode, so I normally have to resort to diagrams.
Meaning of "which conclusion can be drawn"
Because the question is neither "which conclusions can be drawn" nor "can any conclusion be drawn" - the question is saying that there is only one correct conclusion.
D) No Ayes that are not Bees are Seas
The statement is using abbreviated language, making life more difficult.
In full - is the proposition "there are no A's that are not B's are C's" true or false.
Potential ambiguity in "there are no A's that are not B's are C's
Potential meaning one - There are (A's) that are (not B's are C's) - is ungrammatical, therefore ignore.
Potential meaning two - There are (A's that are not B's) that are (C's) - must be what is meant.
It reminds me of the "Four colour map theorem" -
 Alkis Piskas
2.1k
Alkis Piskas
2.1k
What's "Ayes"? I guess it means simply "anyththing" ...Some Ayes are Bees — DavidJohnson
Well, I prefer to "translate" your puzzle-problem into something more meaningful:
Some animals are mammals
All cats are mammals
A) Some animals are cats: True, since mammals are animals (based on the first premise) and cats are mammals
B) Some cats are mammals: False, since we know that "All cats are mammals" (and not only some)
C) No cats are animals: "No cats" is ambiguous - In case it means "none of the cats", then it is false, based on (A)
D) No animals that are not mammals are cats: "No animals" is ambiguous - In case it means "none of the animals" then it is true, since cats are mammals
E) None of the above conclusions can be drawn: False, since there are two true statements, (A) and (D).
(If we reject (D) as ambiguous, then it remains (A) as the only true statement.) -
 TonesInDeepFreeze
3.8kSome animals are cats: True — Alkis Piskas
TonesInDeepFreeze
3.8kSome animals are cats: True — Alkis Piskas
It is true that some animals are cats. But it is not entailed by your premises.
Some cats are mammals: False, — Alkis Piskas
Wrong. In basic logic such as this, 'Some' means one or more. 'Some' does not mean 'Some but not All'.
No cats are animals: "No cats" is ambiguous — Alkis Piskas
Wrong. 'No' means 'none of' and is unambiguous.
there are two true statements, (A) and (D). — Alkis Piskas
(A) is true, but it is not entailed by your premises. -
 TonesInDeepFreeze
3.8kThe problem, noted above, is called undistributed middle. — tim wood
TonesInDeepFreeze
3.8kThe problem, noted above, is called undistributed middle. — tim wood
If by 'above' you mean the sentence you wrote before that one, then, yes, undistributed middle.
But if by 'above' you mean the discussion about Ayes, Bees, and Seas and your thought that (D) is not entailed by the premises, then you still have a severe misconception. An argument may be valid even if its validity is not within the Aristotelian syllogistic forms. -
 TonesInDeepFreeze
3.8kThis is by all appearances an Aristotelian logic game. You appear to admit as much: — tim wood
TonesInDeepFreeze
3.8kThis is by all appearances an Aristotelian logic game. You appear to admit as much: — tim wood
I said no such thing.
The question was "which conclusion can be drawn?" The question was not "which conclusion can be drawn by the method of Aristotelian syllogisms?".
You also more-or-less plainly imply that the law of undistributed middle does not apply. — tim wood
Undistributed middle is a fallacy. I never said otherwise. But that in no way vitiates that from
"All Seas are Bees"
we may validly conclude
"No Ayes that are not Bees are Seas".
Period.
I don't understand why you don't understand that, except that it seems you have stuck in your head that valid inferences regarding "Some, All, and No" must be within the scope of the method of Aristotelian syllogisms.
Now it is for you to demonstrate how it does not apply in any of your standard logics - without adducing premises or information not already provided to make it seem as if it does not. — tim wood
What? It's basic everyday logic. And if that doesn't satisfy you, then one could formalize it in basic symbolic logic.
Indeed, the two salient principles used are Modus Tollens and Monotonicity of Entailment. It's pretty much that simple.
Or in short, how can you say anything categorical about something that has not already been categorically defined - without somehow adding the missing qualifications? — tim wood
I don't know what you think you mean by "categorically defined".
Meanwhile, it is a plain fact that "All Seas are Bees" entails "No Ayes that are not Bees are Seas".
And there are no "qualifications" needed. It is as clear as day in everyday reasoning, and it is as clear as a day on the sun with symbolic logic: Put another way:
Any circumstance in which All Seas are Bees is a circumstance in which No Ayes that are not Bees are Seas.
That is logical entailment.
From the premise "All Seas are Bees" we most certainly can validly draw the conclusion "No Ayes that are not Bees are Seas."
Period.
I already walked you through an English language demonstration of that. Or, I could do it formally in symbolic logic if anyone was captious enough to demand it.
So, in Boolean or first-order or whatever order logic are undistributed middles no longer fallacious? — tim wood
Of course it is a fallacy. But that is not relevant because I am not using that fallacy. I am not arguing in an Aristotelian syllogism. I am not in any way committing undistributed middle, because I'm not even inferring syllogistically.
You really still don't understand this? -
 TonesInDeepFreeze
3.8kDrawn from what? The premises. And what is to be drawn from the premises? A conclusion. — tim wood
TonesInDeepFreeze
3.8kDrawn from what? The premises. And what is to be drawn from the premises? A conclusion. — tim wood
Yes, so what?
you have made it clear that your methods are not those of the problem. — tim wood
False. I already addressed that. Please read again:
The question was "which conclusion can be drawn?" The question was not "which conclusion can be drawn by the method of Aristotelian syllogisms?". — TonesInDeepFreeze
Please do not elide that again. -
 Alkis Piskas
2.1k
Alkis Piskas
2.1k
No, you don't. A dollar is a dollar and cents are cents. Also, you cannot use some vending, gambling etc. machines if you don't have the exact amount of cents.If you have a dollar in your pants pocket, do you (not) have also 32 cents? — tim wood
You are right that you have to infer it, i.e. we don't know that directly, but it is true because its inference is valid, i.e. we can validly conclude it. (Using math sets: Mammals are a subset of animals. Cats are a subset of mammals. That is, cats are a subset of a subset of animals.)A) Some animals are cats: True, since mammals are animals (based on the first premise) and cats are mammals
— Alkis Piskas
You can infer this adding additional information, but you cannot from the premises given validly conclude it. — tim wood -
 RussellA
2.6k
RussellA
2.6k -
 Agent Smith
9.5kSome Ayes are Bees
Agent Smith
9.5kSome Ayes are Bees
All Seas are Bees — DavidJohnson
1. Some Ayes are Bees
2. All Seas are Bees
Ergo,
3. Some Seas may be Bees. -
 Alkis Piskas
2.1k
Alkis Piskas
2.1k
If it is true, well, it is True! That's what I said! :smile:It is true that some animals are cats. But it is not entailed by your premises. — TonesInDeepFreeze
I see what you say: We select one or more cats and say "these (animals) are mammals". This is true. But it refers specifically to "those" cats. Now think also about this: Saying that "some cats are mammals" suggests that there are some cats that are not mammals. Which is of course False, since we know that "All cats are mammals".Some cats are mammals: False,
— Alkis Piskas
Wrong. In basic logic such as this, 'Some' means one or more. 'Some' does not mean 'Some but not All'. — TonesInDeepFreeze
Maybe this is more clear: Can we say "Some persons are humans"? It makes no sense, does it? And it is also false, based on the above reasoning.
Yes, you have already said that! :smile:(A) is true, but it is not entailed by your premises. — TonesInDeepFreeze -
 Alkis Piskas
2.1k
Alkis Piskas
2.1k
:up: Kudos! I wish I had the patience to draw all that! (I only drew it in my mind!)
What I found simpler instead was to "draw" it verbally, in my answer to @tim wood, using math sets as you did:
Mammals are a subset of animals. Cats are a subset of mammals. That is, cats are a subset of a subset of animals.
Which looks exactly what you have drawn on the right...
Now your left drawing shows that only a part of mammals are also animals. This may be correct, if we ignore the fact that we know (ourselves, not from the premises) that mammals refers to animals. That is, in a "possible world", as you say. So, to get rid of this "pitfall", we should change our premises, for example, to:
Some animals have four legs
All cats have four legs
In this case, "four legs" would not refer exclusively to animals, since tables, beds, etc. too have four legs ...
So let's see our statemets:
A) Some animals are cats: Unknown
B) Some cats have four legs: False, since we know that "All cats have four legs" (and not only some)
C) No cats are animals: "No cats" is ambiguous - At best, it's Unknown, based on (A)
D) No animals that have not four legs are cats: "No animals" is ambiguous - Assuming that it means "none of the animals" then it is True, since cats have four legs
E) None of the above conclusions can be drawn: False, if we can accept (D) as True, else True.
It all depends on (D). And this also explains the doubt of the OP, who was not sure about (D) or (E).
Welcome to The Philosophy Forum!
Get involved in philosophical discussions about knowledge, truth, language, consciousness, science, politics, religion, logic and mathematics, art, history, and lots more. No ads, no clutter, and very little agreement — just fascinating conversations.
Categories
- Guest category
- Phil. Writing Challenge - June 2025
- The Lounge
- General Philosophy
- Metaphysics & Epistemology
- Philosophy of Mind
- Ethics
- Political Philosophy
- Philosophy of Art
- Logic & Philosophy of Mathematics
- Philosophy of Religion
- Philosophy of Science
- Philosophy of Language
- Interesting Stuff
- Politics and Current Affairs
- Humanities and Social Sciences
- Science and Technology
- Non-English Discussion
- German Discussion
- Spanish Discussion
- Learning Centre
- Resources
- Books and Papers
- Reading groups
- Questions
- Guest Speakers
- David Pearce
- Massimo Pigliucci
- Debates
- Debate Proposals
- Debate Discussion
- Feedback
- Article submissions
- About TPF
- Help
More Discussions
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum









