Don't need a logic professor.

If x is a C, then x is a B.
Therefore, if x is not a B, then x is not a C.
So, perforce, if x is both an A and not a B, then x is not a C.

That argument involves no assumptions about whether or not there is a something that is an A, B, or C.

Existence matters. Else we willy-nilly prove the existence of God, Zeus, unicorns, and the two-horned rhinoceros sleeping in my bed. You can play the game of if there were..., but neither that rule in general form, or any specific hypothetical are a part of the original problem. And, it asks for a conclusion, not an inference, and those are not quite the same thing.

If, for example, there were As that at the same time are not Bs, then D follows. But that hypothetical is not given. If you assume it, you are adding an assumption. And if there are no such As, then what can you say about something that isn't, except speculatively? You get your D, but only on expanding the terms of the problem. Admittedly in real life a reasonable thing to do.

Conclusion: the answer is "D" and Tim Wood is a vampire no younger than 122 years old. — DavidJohnson

and that only in outdated, Aristotelian categories it's "E", — DavidJohnson

I'm nearer 122 than I like to admit, but I still look pretty good in a mirror. And a small point about Aristotelian logic: Newtonian physics is in many cases still a good and useful approximation, but it's wrong. Aristotelian logic, on the other hand, may be not so useful in some modern applications, but it is not wrong.

The moral of the story is that when playing road-house games for money, it is prudent and certainly wise to check on what, if any, house rules may be in effect.

Else we willy-nilly prove the existence of God, Zeus, unicorns, and the two-horned rhinoceros sleeping in my bed. — tim wood

This argument does not prove the existence of anything.

it asks for a conclusion, not an inference — tim wood

The problem was not what conclusion is true, but rather what conclusion can be drawn from the premises. That is inference.

If, for example, there were As that at the same time are not Bs, then D follows. But that hypothetical is not given. — tim wood

(D) follows from the premises (actually, only one of the premises is needed) no matter what does or does not exists.

I spelled out the logic of the argument explicitly. There is no existence assumption in the argument. Moreover, A's are irrelevant to the argument.

You get your D, but only on expanding the terms of the problem. — tim wood

False. I expanded nothing. I made no assumption other than the premise "All Seas are Beas".

"All Seas are Beas" implies "All non-Beas are non-Seas" implies, perforce, "All things that are both non-Ayes and non-Beas are non-Seas".

And that argument holds whether or not there are Ayes or Beas or Seas.

There is no existence premise nor existence conclusion involved.

/

It is alarming that someone would fail to understand the correctness of the inference, irrespective of training in logic, but rather just as a matter of commonly acquired reasoning.

only in outdated, Aristotelian categories it's "E" — DavidJohnson

Because Aristotelian syllogisms do not exhaust even very basic reasoning.

Aristotelian logic, on the other hand, may be not so useful in some modern applications, but it is not wrong. — tim wood

It's not wrong. It's just that it is nowhere close to covering much of everyday deductive reasoning.

what, if any, house rules may be in effect. — tim wood

The house rules are everyday common reasoning.

All Seas are Beas" implies "All non-Beas are non-Seas" — TonesInDeepFreeze

What if all Seas are real numbers and Beas are complex ñumbers? Are all non-complex numbers non real numbers then?

If all seas are bees, are all non-bees non-seas? If one sea is a bee then a non-bee can still be a sea. Two bees or not two bees, that's the question.

Where can I find more examples as precise as this?

more examples — Josh Alfred

I am afraid the image is not from an "authoritative" source.
I used Microsoft "Paint".
For a few dollars a year one can subscribe to the Forum and be able to upload images onto the Forum - well worth the money.

The picture would have been even more logical if you gave a, b, and c circular forms. Start with c in b (small circle c in circle b). The a, as the biggest circle, around them. Or outside them. Then let a move out (or in).

would D still be a valid conclusion — DavidJohnson

@TonesInDeepFreeze gets to the heart of the matter. Personally, trying to solve in words would make my head explode, so I normally have to resort to diagrams.

Meaning of "which conclusion can be drawn"
Because the question is neither "which conclusions can be drawn" nor "can any conclusion be drawn" - the question is saying that there is only one correct conclusion.

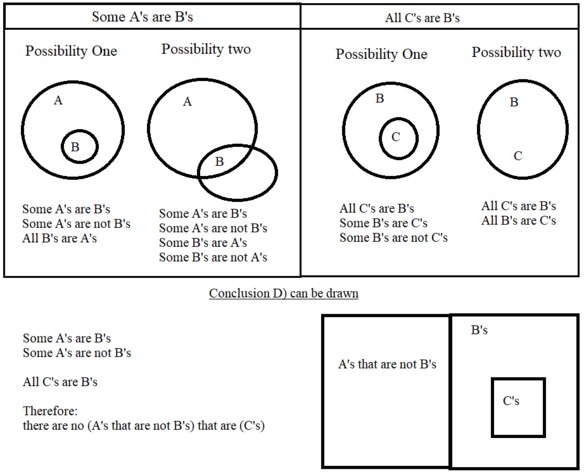
D) No Ayes that are not Bees are Seas
The statement is using abbreviated language, making life more difficult.
In full - is the proposition "there are no A's that are not B's are C's" true or false.

Potential ambiguity in "there are no A's that are not B's are C's
Potential meaning one - There are (A's) that are (not B's are C's) - is ungrammatical, therefore ignore.
Potential meaning two - There are (A's that are not B's) that are (C's) - must be what is meant.



It reminds me of the "Four colour map theorem"

Then let a move — Raymond

Wow! That's exactly what I mean!

It may be an antediluvian point, but usually in Venn diagrams an "x" is included in areas where there is actually a member, to distinguish the area from those where (and when) the existence of a member may be in question, and when the question matters.

Some Ayes are Bees — DavidJohnson

What's "Ayes"? I guess it means simply "anyththing" ...

Well, I prefer to "translate" your puzzle-problem into something more meaningful:

Some animals are mammals
All cats are mammals

A) Some animals are cats: True, since mammals are animals (based on the first premise) and cats are mammals
B) Some cats are mammals: False, since we know that "All cats are mammals" (and not only some)
C) No cats are animals: "No cats" is ambiguous - In case it means "none of the cats", then it is false, based on (A)
D) No animals that are not mammals are cats: "No animals" is ambiguous - In case it means "none of the animals" then it is true, since cats are mammals
E) None of the above conclusions can be drawn: False, since there are two true statements, (A) and (D).

(If we reject (D) as ambiguous, then it remains (A) as the only true statement.)

B) Some cats are mammals: False, since we know that "All cats are mammals" (and not only some) — Alkis Piskas

If you have a dollar in your pants pocket, do you (not) have also 32 cents?

A) Some animals are cats: True, since mammals are animals (based on the first premise) and cats are mammals — Alkis Piskas

You can infer this adding additional information, but you cannot from the premises given validly conclude it. The problem, noted above, is called undistributed middle.

Some animals are cats: True — Alkis Piskas

It is true that some animals are cats. But it is not entailed by your premises.

Some cats are mammals: False, — Alkis Piskas

Wrong. In basic logic such as this, 'Some' means one or more. 'Some' does not mean 'Some but not All'.

No cats are animals: "No cats" is ambiguous — Alkis Piskas

Wrong. 'No' means 'none of' and is unambiguous.

there are two true statements, (A) and (D). — Alkis Piskas

(A) is true, but it is not entailed by your premises.

The problem, noted above, is called undistributed middle. — tim wood

If by 'above' you mean the sentence you wrote before that one, then, yes, undistributed middle.

But if by 'above' you mean the discussion about Ayes, Bees, and Seas and your thought that (D) is not entailed by the premises, then you still have a severe misconception. An argument may be valid even if its validity is not within the Aristotelian syllogistic forms.

Some Ayes are Bees
All Seas are Bees
Which conclusion can be drawn? — DavidJohnson

This is by all appearances an Aristotelian logic game. You appear to admit as much:

An argument may be valid even if its validity is not within the Aristotelian syllogistic forms. — TonesInDeepFreeze

Your conclusion then imo out of bounds. You also more-or-less plainly imply that the law of undistributed middle does not apply. Within Aristotelian logic it certainly does. Now it is for you to demonstrate how it does not apply in any of your standard logics - without adducing premises or information not already provided to make it seem as if it does not.

Or in short, how can you say anything categorical about something that has not already been categorically defined - without somehow adding the missing qualifications? If you infer them, then terminology aside, you have reached a conclusion of sorts, an inferential conclusion. But not one supported by, or supportable within - as you make clear - '"the Aristotelian syllogistic forms."

So, in Boolean or first-order or whatever order logic are undistributed middles no longer fallacious?

This is by all appearances an Aristotelian logic game. You appear to admit as much: — tim wood

I said no such thing.

The question was "which conclusion can be drawn?" The question was not "which conclusion can be drawn by the method of Aristotelian syllogisms?".

You also more-or-less plainly imply that the law of undistributed middle does not apply. — tim wood

Undistributed middle is a fallacy. I never said otherwise. But that in no way vitiates that from

"All Seas are Bees"

we may validly conclude

"No Ayes that are not Bees are Seas".

Period.

I don't understand why you don't understand that, except that it seems you have stuck in your head that valid inferences regarding "Some, All, and No" must be within the scope of the method of Aristotelian syllogisms.

Now it is for you to demonstrate how it does not apply in any of your standard logics - without adducing premises or information not already provided to make it seem as if it does not. — tim wood

What? It's basic everyday logic. And if that doesn't satisfy you, then one could formalize it in basic symbolic logic.

Indeed, the two salient principles used are Modus Tollens and Monotonicity of Entailment. It's pretty much that simple.

Or in short, how can you say anything categorical about something that has not already been categorically defined - without somehow adding the missing qualifications? — tim wood

I don't know what you think you mean by "categorically defined".

Meanwhile, it is a plain fact that "All Seas are Bees" entails "No Ayes that are not Bees are Seas".

And there are no "qualifications" needed. It is as clear as day in everyday reasoning, and it is as clear as a day on the sun with symbolic logic: Put another way:

Any circumstance in which All Seas are Bees is a circumstance in which No Ayes that are not Bees are Seas.

That is logical entailment.

From the premise "All Seas are Bees" we most certainly can validly draw the conclusion "No Ayes that are not Bees are Seas."

Period.

I already walked you through an English language demonstration of that. Or, I could do it formally in symbolic logic if anyone was captious enough to demand it.

So, in Boolean or first-order or whatever order logic are undistributed middles no longer fallacious? — tim wood

Of course it is a fallacy. But that is not relevant because I am not using that fallacy. I am not arguing in an Aristotelian syllogism. I am not in any way committing undistributed middle, because I'm not even inferring syllogistically.

You really still don't understand this?

Which conclusion can be drawn? — DavidJohnson

Drawn from what? The premises. And what is to be drawn from the premises? A conclusion.

You have inferentially argued a true proposition. And I have no problem with that in itself. But you have made it clear that your methods are not those of the problem. And that's your blind spot - as if being asked to untie a knot, you cut it with a knife, and see no problem. As we're at sixes and sevens, I suggest we leave it here. You may have the last word if you want it.

Drawn from what? The premises. And what is to be drawn from the premises? A conclusion. — tim wood

Yes, so what?

you have made it clear that your methods are not those of the problem. — tim wood

False. I already addressed that. Please read again:

The question was "which conclusion can be drawn?" The question was not "which conclusion can be drawn by the method of Aristotelian syllogisms?". — TonesInDeepFreeze

Please do not elide that again.

If you have a dollar in your pants pocket, do you (not) have also 32 cents? — tim wood

No, you don't. A dollar is a dollar and cents are cents. Also, you cannot use some vending, gambling etc. machines if you don't have the exact amount of cents.

A) Some animals are cats: True, since mammals are animals (based on the first premise) and cats are mammals
— Alkis Piskas
You can infer this adding additional information, but you cannot from the premises given validly conclude it. — tim wood

You are right that you have to infer it, i.e. we don't know that directly, but it is true because its inference is valid, i.e. we can validly conclude it. (Using math sets: Mammals are a subset of animals. Cats are a subset of mammals. That is, cats are a subset of a subset of animals.)

I prefer to "translate" your puzzle-problem into something more meaningful: — Alkis Piskas

Some Ayes are Bees
All Seas are Bees — DavidJohnson

1. Some Ayes are Bees
2. All Seas are Bees
Ergo,
3. Some Seas may be Bees.

It is true that some animals are cats. But it is not entailed by your premises. — TonesInDeepFreeze

If it is true, well, it is True! That's what I said! :smile:

Some cats are mammals: False,
— Alkis Piskas
Wrong. In basic logic such as this, 'Some' means one or more. 'Some' does not mean 'Some but not All'. — TonesInDeepFreeze

I see what you say: We select one or more cats and say "these (animals) are mammals". This is true. But it refers specifically to "those" cats. Now think also about this: Saying that "some cats are mammals" suggests that there are some cats that are not mammals. Which is of course False, since we know that "All cats are mammals".
Maybe this is more clear: Can we say "Some persons are humans"? It makes no sense, does it? And it is also false, based on the above reasoning.

(A) is true, but it is not entailed by your premises. — TonesInDeepFreeze

Yes, you have already said that! :smile:

:up: Kudos! I wish I had the patience to draw all that! (I only drew it in my mind!)
What I found simpler instead was to "draw" it verbally, in my answer to @tim wood, using math sets as you did:
Mammals are a subset of animals. Cats are a subset of mammals. That is, cats are a subset of a subset of animals.
Which looks exactly what you have drawn on the right...
Now your left drawing shows that only a part of mammals are also animals. This may be correct, if we ignore the fact that we know (ourselves, not from the premises) that mammals refers to animals. That is, in a "possible world", as you say. So, to get rid of this "pitfall", we should change our premises, for example, to:

Some animals have four legs
All cats have four legs

In this case, "four legs" would not refer exclusively to animals, since tables, beds, etc. too have four legs ...

So let's see our statemets:
A) Some animals are cats: Unknown
B) Some cats have four legs: False, since we know that "All cats have four legs" (and not only some)
C) No cats are animals: "No cats" is ambiguous - At best, it's Unknown, based on (A)
D) No animals that have not four legs are cats: "No animals" is ambiguous - Assuming that it means "none of the animals" then it is True, since cats have four legs
E) None of the above conclusions can be drawn: False, if we can accept (D) as True, else True.

It all depends on (D). And this also explains the doubt of the OP, who was not sure about (D) or (E).