-
 Count Timothy von Icarus
4.3k
Count Timothy von Icarus
4.3k
Didn't I just tell you that what I am doing is expressing skepticism, and not making claims about what does and doesn't objectively exist?
Ok, that makes more sense. I had thought these were supposed to be good reasons for rejecting platonism, not simply not affirming it.
However, it does seem like you have made "objective knowledge" apply to essentially nothing. Mathematics, the natural sciences, world history, the rules of chess, presumably metaphysics as well, will not qualify. And it seems to me that even the notion of the existence of any reality "behind the veil of appearances" also falls victim to this lack of objectivity. It too might be something that only appears like a real distinction, but perhaps it isn't e.g. Shankara, there is only Brahma, even maya.
There is "logic" as formal systems of the sort you listed, but also logic as "good reasoning" more generally (rhetoric was long part of logic), "logic" as the "rules of thought," the "discourse of the soul," and "logic" as the logos of the world, its intelligibility and rationality. I would assume platonists often are looking to some of the broader conceptions instead of a narrow, formal one.
I don't think it makes any sense to say that they platonistically exist in New Foundations but don't platonistically exist in ZFC. We can only take the approach of mathematical fictionalism and say that they exist according to New Foundations but not according to ZFC.
You're probably right in many cases, but I have seen the systems themselves proposed as platonic objects. So both can be right because both are really just descriptions of a mathematical object. For instance, Tegmark's Mathematical Universe Hypothesis, which is fairly opaque on some of the more philosophical elements, takes a very broad view of mathematical objects.
Tegmark brings to mind another view, ontic structural realism. Things just are the math that fundamentally describes them. This seems to me to be, if not a type of platonism, then something quite close, and it seems not unpopular in the physics community (although certainly not a majority view or anything like that). The question: "which sorts of mathematical objects exist" is various answered as "all of them" or "just the computable ones" (with efforts to try to justify the latter position being, IMO, unconvincing). -
 Joshs
6.7k
Joshs
6.7k
So you're saying that math can be a community construction without necessarily arising from any activity involving the world. It's that what we call the world conforms to thought a la the Tractatus, so it's no surprise that we find an affinity between our math and the world's shenanigans.
Do you believe that we are also products of analysis? That your individuality arises from reflection on events? — frank
I was thinking of the later Wittgenstein rather than the Tractatus, but yes, math would be a community construction. It’s not that the world isn’t involved, it’s just that the world only reaches us through our constructive interactions with it. We are an intrinsic part of the world, and the Real is the effect of a two-way interaction.
I believe my individual authonomy as a subject is a product of my partially shared interactions with others. -
 Tzeentch
4.4kHowever, it does seem like you have made "objective knowledge" apply to essentially nothing. — Count Timothy von Icarus
Tzeentch
4.4kHowever, it does seem like you have made "objective knowledge" apply to essentially nothing. — Count Timothy von Icarus
Which is essentially platonic, and that's exactly my objection to people using the term 'mathematical platonism'.
I'm not rejecting platonism. I'm pointing out that it's being misappropriated here. -
 J
2.4kWell, let's fill it in.
J
2.4kWell, let's fill it in.
Harry: According to me, propositions exist.
Sally: According to me, propositions do not exist.
Is their dispute about propositions, or about the meaning of 'exist'? For the moment, let's not worry about which way of seeing it is closer to what mathematical fictionists are saying. What answer would you be inclined to give? -
 Count Timothy von Icarus
4.3k
Count Timothy von Icarus
4.3k
I think Plotinus is informative since he brings up this line of reasoning and uses it to reject truth as simple correspondence. If truth is the correspondence of phenomenal awareness to a sort of noumenal being, then one can never know truth because one can never "step outside of experience," in order to compare the two. But Plotinus (and I see him as following Plato here) simply rejects this notion of truth and substitutes what might be called an identity theory.
Forms, then, are the very ‘whatnesses’ of things that enable them to be anything at all. Without such identities or whatnesses, without forms, there is no truth, nothing is anything, and there is no reality...
Here, then, we have Plato’s answer to the age-old question, τι τὸ ὄν, “What is being?” Being, τὸ ὄν, that which is, is εἶδος, form, the looks in things that are there to be seen by intellect and in virtue of which anything has any identity, any intelligibility, and hence any reality at all. Henceforward, not only in Plato but throughout the philosophical tradition we are considering, οὐσία will mean not simply ‘reality’ in an unspecified sense, but, more precisely, reality qua that which is intelligible. Being, as what is given to thought, consists of ‘looks,’ that is, intelligible whatnesses, identities, ideas, that show up
in varying connections and contexts, and thus lend a share of intelligibility, and hence of reality, to the world around us...
But neither is being ‘mind-independent,’ as if it were prior to and could exist without, or in separation from, intellect. There is no thought without being, but neither is there any being without thought. In order to avoid subjectivism, it is necessary, as Plotinus says, “to think being prior to intellect” (V.9.8.11–12), but this is only because in our imperfect, discursive thinking they are “divided by us” (V.9.8.20–21), whereas in truth they are“one nature” (V.9.8.17). Neither thinking nor being is prior or posterior to the other, for, just in that thinking is the apprehension of being and being is what is apprehended by thought, they are ontologically simultaneous: “Each of them [i.e., each being] is intellect and being, and the all-together is all intellect and all being, intellect in thinking establishing being, and being in being thought giving to intellect thinking and existence … These are simultaneous [ἅμα] and exist together [συνυπάρχει] and do not abandon each other, but this one is two, at once [ὁμου] intellect and being, that which thinks and that which is thought, intellect as thinking and being as that which is thought” (V.1.4.26–34).
Eric Perl - Thinking Being
I find this to be almost the inversion of the modern supposition that we must be skeptical because we cannot "get outside thought." This is why mathematical knowledge, dianoia, occupies the highest portion on the Divided Line below the Forms themselves. Noesis (immediate intuition, apprehension, or mental 'seeing' of principles) is not "stepping outside thought to thoughtless reality" either.
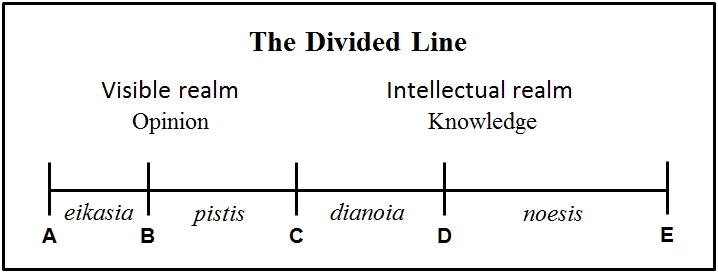
-
 Count Timothy von Icarus
4.3k
Count Timothy von Icarus
4.3k
They need to define their terms. There is a fairly controversial, obvious sense in which propositions exist. "Exist as 'abstract objects?'" Then what said is probably something like what is going on. They might even be agreement and just dealing with ambiguity and equivocation.
"Exist mind-independently" is also unhelpful if undefined, and the same goes for "objective." There is an obvious sense in which propositions cannot be mind-independent (we are speaking and thinking of them) and on the common dictionary usage of "objective" they would seem to exist "objectively," yet often "objective" is used to denote something like "noumenal."
So they might be in disagreement about a great many things. The problem with going off the SEP summary sentence ITT is that it does not define its terms. For instance, I would imagine that many Platonists (capital P) would deny that anything has the sort of "mind-independent" existence that some contemporary philosophers would take them to be arguing for. That is, this "mind-independence" would be a bad definition, since for anything to be anything at all it has to have some intelligible eidos, although surely they also do not mean "rocks disappear when no one is looking at them or thinking about them," either. -
 frank
19kIt’s not that the world isn’t involved, it’s just that the world only reaches us through our constructive interactions with it. — Joshs
frank
19kIt’s not that the world isn’t involved, it’s just that the world only reaches us through our constructive interactions with it. — Joshs
Right. That's along the lines of what I was saying. Although, that's just a gesture at explaining why math helps us predict events. It's when we take individual cases, like Fibonacci numbers, that we find we haven't explained anything. Yet. -
 Tzeentch
4.4kFor instance, I would imagine that many Platonists (capital P) would deny that anything has the sort of "mind-independent" existence that some contemporary philosophers would take them to be arguing for. — Count Timothy von Icarus
Tzeentch
4.4kFor instance, I would imagine that many Platonists (capital P) would deny that anything has the sort of "mind-independent" existence that some contemporary philosophers would take them to be arguing for. — Count Timothy von Icarus
It is because they believed 'mind' (nous, if memory serves me right) emanates from the One, and it is through participation in this quality that we are able to gain an understanding of matters that goes beyond sense perception. The quality must exist as some form of emanation from the One for us to be able to participate in it.
Plato and certainly Neoplatonists like Plotinus were quite mystical in their beliefs, where they believed experiences of higher realities were possible, but exceedingly difficult to describe because they encompassed qualities that preceded nous or the intellect, and were, literally, unintelligible.
In a nutshell, 'mathematical platonism' would suggest people have experienced these higher realities and found mathematics to be existing within them. -
 Joshs
6.7kRight. That's along the lines of what I was saying. Although, that's just a gesture at explaining why math helps us predict events. It's when we take individual cases, like Fibonacci numbers, that we find we haven't explained anything. Yet. — frank
Joshs
6.7kRight. That's along the lines of what I was saying. Although, that's just a gesture at explaining why math helps us predict events. It's when we take individual cases, like Fibonacci numbers, that we find we haven't explained anything. Yet. — frank
There was a famous confrontation between Wittgenstein and Godel that has been interpreted in different ways. The way I see it, Wittgenstein honed in on the idea that something like an incompleteness theorem could be ‘proved’. What is it we are doing when we prove that sort of theorem, or for that matter, any theorem, as ‘true’?One thing that we don’t think we are doing is changing the subject. That is, we think of mathematical proof as a paradigmatic example of rational thought, which allows us to link premises with outcomes in reliable ways. The source of this reliability is the assumed persistence of meaning of the premises. We depend on the working parts of logical calculation retaining their identity over the course of the calculation.
But what we don’t assume is that when working through something like a mathematical or logical proof, we surreptitiously import new assumptions, changing in a very subtle manner the stakes and the sense of our task as we move through its. steps. The production of Fibonacci numbers is one example of what happens when we do different things with numbers, like create rational out of real numbers. All sorts of new surprises ensue. Not because such things are built into number itself, but because we are changing the subject in a subtle way, importing new concepts into our use of numbers. It is what we are constructing and importing that confronts us with unexplainable riddles, because , believing that each new wrinkle belongs to the ‘same’ system as the old, we are trying to derive our new invention from a previous one. This is what we hope to do when we talk about ‘explaining’ Fibonacci numbers. -
 Wayfarer
26.1kIn a nutshell, 'mathematical platonism' would suggest people have experienced these higher realities and found mathematics to be existing within them. — Tzeentch
Wayfarer
26.1kIn a nutshell, 'mathematical platonism' would suggest people have experienced these higher realities and found mathematics to be existing within them. — Tzeentch
Here is a passage about Augustine which details the Platonist insights that inspired his religious conversion.
During his Manichaean period Augustine’s attention had been focused on the external corporeal world. His thinking had consequently been bound by sensory experience: he could conceive only what he could form a sensory image of. Platonism, however, admonished him to abandon the corporeal world and turn inward, using the eye of his own rational soul. When he did so, he discovered an astonishing new realm. The incorporeality, immutability, and eternity that characterize purely intellectual thought are the clues that led Augustine, by stages, to the divine nature itself.
Augustine begins by establishing a hierarchy that sorts into general categories and ranks the natures that comprise the universe: existence, life, and understanding:
Therefore the nature that merely exists (and neither lives nor understands) ranks below the nature that not only exists but also lives (but does not understand) – the soul of the non-human animals is of this sort. This nature in turn ranks below the nature that at once exists, lives, and understands – for example, the rational mind of the human being. (lib. arb. 2.6.13)
His strategy will be to argue that there is a nature that ranks above the rational mind of the human being, a nature that he will identify as divine (lib. arb. 2.6.14, 2.15.39). In order to discover it, he ascends the hierarchy of natures, turning attention first from bodies (the first and lowest-ranking category in the hierarchy) to the soul (psuche, the nature constitutive of both the second and third categories), and then within his own soul from the sensory (found in both human beings and the non-human animals) to the rational: “a kind of head or eye of our soul ... which does not belong to the nature of non-human animals” (lib. arb. 2.6.13).11
Having ascended as far as reason – that which is highest in us – he focuses on reason’s distinctive perceptual capacities and the distinctive sorts of objects they put us in contact with, the objects of pure thought. By way of example, Evodius, Augustine’s interlocutor in the dialogue, first suggests that they consider “the structure and truth of number,” by which he means arithmetical facts and relationships of the sort expressed by such truths as “seven plus three equals ten” (lib. arb. 2.8.20–21). Augustine himself adds the example of the indivisible mathematical unit that is the foundation of all number. He later introduces into the discussion a collection of a priori evaluative and normative truths such as “wisdom should be diligently sought after,” “inferior things should be subjected to superior things,” and “what is eternal is better than what is temporal” (lib. arb. 2.10.28). He thinks of these truths as constitutive of wisdom itself and therefore normative for anyone who would possess it. Moreover, anyone who is able to contemplate them will recognize their truth. Examination of these various examples leads Augustine to three conclusions: intelligible objects of these sorts are independent of our minds, incorporeal, and higher than reason. Put briefly, the main lines of his reasoning are as follows (lib. arb. 2.8.20–12.34):
1. Intelligible objects must be independent of particular minds because they are common to all who think. In coming to grasp them, an individual mind does not alter them in any way, it cannot convert them into its exclusive possessions or transform them into parts of itself. Moreover, the mind discovers them rather than forming or constructing them, and its grasp of them can be more or less adequate. Augustine concludes from these observations that intelligible objects must exist independently of individual human minds.
2. Intelligible objects must be incorporeal because they are eternal and immutable. By contrast, all corporeal objects, which we perceive by means of the bodily senses, are contingent and mutable. Moreover, certain intelligible objects – for example, the indivisible mathematical unit – clearly cannot be found in the corporeal world (since all bodies are extended, and hence divisible). These intelligible objects cannot therefore be perceived by means of the senses; they must be incorporeal and perceptible by reason alone.
3. Intelligible objects must be higher than reason because they judge reason. Augustine means by this that these intelligible objects constitute a normative standard against which our minds are measured (lib. arb. 2.5.12 and 2.12.34). We refer to mathematical objects and truths to judge whether or not and to what extent our minds understand mathematics. We consult the rules of wisdom to judge whether or not and to what extent a person is wise. In virtue of their normative relation to reason, Augustine argues that these intelligible objects must be higher than it, as a judge is higher than what it judges. Moreover, the intrinsic nature of these objects shows them to be higher than reason. They are eternal and immutable; by contrast, the human mind is clearly mutable. Augustine holds that since it is evident to all who consider it that the immutable is superior to the mutable (it is among the rules of wisdom he identifies), it follows that these objects are higher than reason.
...By focusing on objects perceptible by the mind alone and by observing their nature, in particular their eternity and immutability, Augustine came to see that certain things that clearly exist, namely, the objects of the intelligible realm, cannot be corporeal. When he cries out in the midst of his vision of the divine nature, “Is truth nothing just because it is not diffused through space, either finite or infinite?” (FVP 13–14), he is acknowledging that it is the discovery of intelligible truth that first frees him to comprehend incorporeal reality. — Cambridge Companion to Augustine -
 Wayfarer
26.1kI've discovered a Notre Dame Review about a book which I'll probably never get around to, but which finds some common ground between Platonism and Husserl, Phenomenology, Logic and the Philosophy of Mathematics, Richard Tieszen, from which:
Wayfarer
26.1kI've discovered a Notre Dame Review about a book which I'll probably never get around to, but which finds some common ground between Platonism and Husserl, Phenomenology, Logic and the Philosophy of Mathematics, Richard Tieszen, from which:
In his later Ideas for a Pure Phenomenology and Phenomenological Philosophy (1913), Husserl develops the method of eidetic variation. Eidetic variation consists of a series of mental acts that aim to grasp an invariant, ideal, non-sensory object that serves as a substrate to a range of experiences. The same object is given across this range of experience and we experience its self-samenesss. Husserl suggested that this method would serve to sharpen our conceptual grasp of ideal objects, and Tieszen argues that this method is in fact close to the actual procedure employed in modern geometry. In abstract sciences, Tieszen writes, "objectivity and invariance go hand in hand" (p. 89), and invariance is best understood as givenness. An ontology of abstract objects, then, should rest on the elements of Husserlian epistemology.
Husserl called his position "transcendental" phenomenology, and Tieszen makes sense of this by claiming that it can be seen as an extension of Kant's transcendental idealism. The act of cognition constitutes its content as objective. Once we recognize the distinctive givenness of essences in our experience, we can extend Kant's realism about empirical objects grounded in sensible intuition to a broader realism that encompasses objects grounded in categorial intuition, including mathematical objects.
The view is very much like what Kant has to say about empirical objects and empirical realism, except that now it is also applied to mathematical experience. On the object side of his analysis Husserl can still claim to be a kind of realist about mathematical objects, for mathematical objects are not our own ideas (p. 57f.).
This view, Tieszen points out, can preserve all the advantages of Platonism with none of its pitfalls. We can maintain that mathematical objects are mind-independent, self-subsistent and in every sense real, and we can also explain how we are cognitively related to them: they are invariants in our experience, given fulfillments of mathematical intentions. The evidence that justifies our mathematical knowledge is of the same kind as the evidence available for empirical knowledge claims: we are given these objects. And, since they are given, not subjectively constructed, fictionalism, conventionalism, and similar compromise views turn out to be unnecessarily permissive. The only twist we add to a Platonic realism is that ideal objects are transcendentally constituted.
We can evidently say, for example, that mathematical objects are mind-independent and unchanging, but now we always add that they are constituted in consciousness in this manner, or that they are constituted by consciousness as having this sense … . They are constituted in consciousness, nonarbitrarily, in such a way that it is unnecessary to their existence that there be expressions for them or that there ever be awareness of them. (p. 13).
Bolds added. It is in accordance with my intuitive understanding. -
 SophistiCat
2.4kSophistiCat Could you explain the thing about the number 1/137 in physics? — frank
SophistiCat
2.4kSophistiCat Could you explain the thing about the number 1/137 in physics? — frank
Not sure why the question is addressed to me - did I write something about this before? Anyway, this is more of a counterexample to the point being made (if we consider something like Fibonacci numbers as a paradigmatic supporting example). In the Standard Model of particle physics, there is a fundamental constant known as the fine structure constant. The interesting thing about it is that it is dimensionless, i.e., it is a number that does not depend on units of measurement - nor on anything else for that matter. (Avogadro number is also dimensionless, but unlike the fine structure constant, it depends on some arbitrarily chosen dimensional parameters, such as volume, temperature and pressure.) What was even more intriguing back when that constant was proposed was that, within the accuracy of early measurements, the number looked simple without being trivial: not 1 or 2 or some multiple of pi or e, but as close as permitted by early measurements to the ratio 1/137 (Avogadro number is ~6.023x1023). For that reason, physicists puzzled over the possible significance of that ratio. This led to some unfortunate numerology - long since abandoned - that grew ever more convoluted as later, more accurate measurements no longer quite fit that initial 1/137 estimate.
Such speculation may look silly in retrospect, but it should be understood within its historical context. Physicists, probably more than anyone else in science, are obsessed with simplicity, unification and "naturalness," and not without reason, because this attitude has accompanied spectacular advances in physics over the past two centuries. But how philosophically justified is it? And how sustainable? I suppose that goes to the question of the proverbial "unreasonable effectiveness of mathematics." -
 J
2.4k
J
2.4k
Count T's answer -- that Harry and Sally need to define their terms -- is the direction in which I was going. With all respect to Michael, we have no way of knowing whether H & S are disputing platonism until we get an answer to the question I posed. I was hoping to develop this thought in a dialogic fashion, but I'll go ahead and just say what I mean.
Two accounts of the Harry/Sally dispute are possible.
In the first, H & S share a common understanding of how they're going to use the term 'exist'. Either they live in a cultural community in which this is taken for granted, or -- better, for our purposes -- they have a preliminary conversation in which they discover that they do indeed mean the same thing by 'exist'. So if they're having a dispute, as we imagine them doing, it must be over what a proposition is. They're in full agreement about what it means for something to exist, but they differ about what sort of thing a proposition is -- what its characteristics and qualities are. Thus, Harry, using his ideas about propositions, makes the case that they exist; Sally, using hers, that they don't.
In the second, the reverse is the case. H & S share a common understanding of what a proposition is -- again, we can picture them determining this beforehand. So if a dispute is occurring, it must be over what it means for something to exist. They're in full agreement about the "characteristics and qualities" of a proposition -- how to use the word, how to recognize one, what functions it serves -- but they differ about whether existence can be ascribed to that sort of thing.
(Yes, this little story is about the existential quantifier, ∃, and quantifier variance, but I'm trying to avoid Logicalese so as to keep it accessible.)
So what does this have to do with platonism, and in particular with the idea that only one type of quantification could be countenanced in a world of mathematical platonism?
Let's look again at Michael's suggestion that, depending upon which version of logic/math you're using, certain items would either exist or not exist:
We can only take the approach of mathematical fictionalism and say that they [the items in question] exist according to New Foundations but not according to ZFC. — Michael
Now apply the "Harry and Sally question": Is the mathematical fictionalist saying that New Foundations and ZFC share the same meaning for 'exist' but differ about whether the items in question qualify? That, I think, is Michael's meaning. But we can now see that it's equally possible for the mathematical fictionalist to claim that New Foundations and ZFC differ about what 'exists' means. They may share the same understanding of, say, what a Quine atom is, but because they don't agree about existence, their conclusions are different.
To simplify, we can either hold X steady and differ about existence, or we can hold 'existence' steady and differ about X.
So what I'm saying is that one version of mathematical platonism will indeed have room for only one correct logic, because it will be a logic that debars certain entities from existing at all. Those other, renegade logics would have to be "man-made." But another, equally reasonable version of math platonism will be liberal or agnostic about different uses of 'exist', so that both New Foundations and ZFC, e.g., may be "found" in the platonic world.
This all circles back to my question about how correctness has a bearing on the plausibility of mathematical platonism -- whether math platonism requires a single correct logic for it to be plausible. It seems that two incompatible logics could both be found as objects of mathematical platonism. For:
I don't think it makes any sense to say that they platonistically exist in New Foundations but don't platonistically exist in ZFC. — Michael
but if my argument is sound, then it does make sense after all. That's because now we're no longer fooled by seeing the word 'exist' occurring twice and believing it must mean the same thing each time. It may or it may not. But if the use of 'exist' itself is not consistent, then anything goes, platonically. We can't put a fence around it by using an operator like "according to Y" or "to Z" because we don't know Y and Z's account of existence. Either, or both, of them may be claiming that its own version is compatible with quantifier variance. -
 Wayfarer
26.1kPhysicists, probably more than anyone else in science, are obsessed with simplicity, unification and "naturalness," and not without reason, because this attitude has accompanied spectacular advances in physics over the past two centuries. But how philosophically justified is it? And how sustainable? I suppose that goes to the question of the proverbial "unreasonable effectiveness of mathematics." — SophistiCat
Wayfarer
26.1kPhysicists, probably more than anyone else in science, are obsessed with simplicity, unification and "naturalness," and not without reason, because this attitude has accompanied spectacular advances in physics over the past two centuries. But how philosophically justified is it? And how sustainable? I suppose that goes to the question of the proverbial "unreasonable effectiveness of mathematics." — SophistiCat
Subject of a book by Sabine Hossenfelder, Lost in Math.
Whether pondering black holes or predicting discoveries at CERN, physicists believe the best theories are beautiful, natural, and elegant, and this standard separates popular theories from disposable ones. This is why, Sabine Hossenfelder argues, we have not seen a major breakthrough in the foundations of physics for more than four decades.
The belief in beauty has become so dogmatic that it now conflicts with scientific objectivity: observation has been unable to confirm mindboggling theories, like supersymmetry or grand unification, invented by physicists based on aesthetic criteria. Worse, these "too good to not be true" theories are actually untestable and they have left the field in a cul-de-sac. To escape, physicists must rethink their methods. Only by embracing reality as it is can science discover the truth.
(Although from my perspective, embracing reality 'as it is' will entail abandoning the axiom that it is only physical.) -
 frank
19kNot sure why the question is addressed to me - did I write something about this before? — SophistiCat
frank
19kNot sure why the question is addressed to me - did I write something about this before? — SophistiCat
No, it's that you're a reliable source for information about physics.
This led to some unfortunate numerology - long since abandoned - that grew ever more convoluted as later, more accurate measurements no longer quite fit that initial 1/137 estimate. — SophistiCat
Oh. So it's not really significant? Good to know. :grin: Thank you! -
 Joshs
6.7k
Joshs
6.7k
We can maintain that mathematical objects are mind-independent, self-subsistent and in every sense real, and we can also explain how we are cognitively related to them: they are invariants in our experience, given fulfillments of mathematical intentions. The evidence that justifies our mathematical knowledge is of the same kind as the evidence available for empirical knowledge claims: we are given these objects. And, since they are given, not subjectively constructed, fictionalism, conventionalism, and similar compromise views turn out to be unnecessarily permissive. The only twist we add to a Platonic realism is that ideal objects are transcendentally constituted.
We can evidently say, for example, that mathematical objects are mind-independent and unchanging, but now we always add that they are constituted in consciousness in this manner, or that they are constituted by consciousness as having this sense … . They are constituted in consciousness, nonarbitrarily, in such a way that it is unnecessary to their existence that there be expressions for them or that there ever be awareness of them. (p. 13).
Mathemarical concepts for Husserl are no more ‘real’ than the spatial objects we interact with in the world. That is to say, their reality is the result of an abstractive idealization on the part of the subject, drawing from encounters with concrete data but imposing on those contents an idealized form. Derrida explains:
Numbers are mental creations insofar as they form the results of activities exercised upon concrete contents; what these activities create, however, are not new and absolute contents which we could find again in space or in the 'external world'; rather are they unique relation-concepts which can only be produced again and again and which are in no way capable of being found somewhere ready-made." This remarkable passage, which already designates the production, therefore the primordial historicity, of idealities which no longer will ever belong to the time and space of empirical history, is from Concerning the Concept of Number (1887), which is taken up again as the first chapter of Philosophy of Arithmetic (1891) -
 Wayfarer
26.1kWe can maintain that mathematical objects are mind-independent, self-subsistent and in every sense real, and we can also explain how we are cognitively related to them: they are invariants in
Wayfarer
26.1kWe can maintain that mathematical objects are mind-independent, self-subsistent and in every sense real, and we can also explain how we are cognitively related to them: they are invariants inour experienceconsciousness
Rather like objects as ‘permanent possibilities of sensation’ but here the objects are noumenal. -
 Janus
18kThe evidence that justifies our mathematical knowledge is of the same kind as the evidence available for empirical knowledge claims: we are given these objects.And, since they are given, not subjectively constructed, fictionalism, conventionalism, and similar compromise views turn out to be unnecessarily permissive. The only twist we add to a Platonic realism is that ideal objects are transcendentally constituted.
Janus
18kThe evidence that justifies our mathematical knowledge is of the same kind as the evidence available for empirical knowledge claims: we are given these objects.And, since they are given, not subjectively constructed, fictionalism, conventionalism, and similar compromise views turn out to be unnecessarily permissive. The only twist we add to a Platonic realism is that ideal objects are transcendentally constituted.
We can evidently say, for example, that mathematical objects are mind-independent and unchanging, but now we always add that they are constituted in consciousness in this manner, or that they are constituted by consciousness as having this sense … . They are constituted in consciousness, nonarbitrarily, in such a way that it is unnecessary to their existence that there be expressions for them or that there ever be awareness of them. (p. 13).
It is in accordance with my intuitive understanding. — Wayfarer
It doesn't sound like your view. since you are always arguing that reality is entirely constructed by consciousness, and that it is meaningless to speak of concrete things having an independent existence. It is clearly stated in this article that they do have an independent existence, and I think the implication there is that the non-arbitrary way in which consciousness models objects is the best evidence we have for their independent existence. -
 Wayfarer
26.1ksince you are always arguing that reality is entirely constructed by consciousness — Janus
Wayfarer
26.1ksince you are always arguing that reality is entirely constructed by consciousness — Janus
I never have used that expression nor would I put it like that //although on reflection I suppose it is fair//.
What I do say is that material objects are perceived by the senses and so can’t be truly mind-independent, because sense data must be interpreted by the mind for any object to be cognised. What interests me about the passage I quoted, is that mathematical functions and the like are not the product of your or my mind, but can only be grasped by a mind. That’s the sense in which they’re what Augustine describes as ‘intelligible objects’ in the earlier post about that.
The underlying argument is very simple - it is that number is real but not materially existent. And reason Platonism is so strongly resisted is because it is incompatible withmaterialismnaturalism on those grounds, as per the passage from the Smithsonian article upthread, ‘What is Math?’: 'The idea of something existing “outside of space and time” makes empiricists nervous.' -
 J
2.4kdrawing from encounters with concrete data — Joshs
J
2.4kdrawing from encounters with concrete data — Joshs
activities exercised upon concrete contents
What might be some examples of the concrete contents or data? Is the implication that there is some level of sense impression which is not mediated by ideas or "abstractive idealization"? This connects with the thread awhile back about scheme/content distinctions, especially this:
The alternative, more robust scheme-content distinction Wang proposes involves what he calls “common-sense experience” (this plays the role of content) and whatever conceptual scheme may be in play among a given community. What is key here is that, for Wang, common-sense experience (which he also calls “thick experience,” drawing from James) is not “innocent” of theoretical influence. It is not the same thing as a Kantian/Quinian uninterpreted world of sense-data or things-as-they-are. Our basic experience, the most basic one possible (and this will prove to be crucial), is already theory-laden. — J
So the question I'm posing is whether the "concrete data" are pre-theoretical, which Wang thinks is not possible. Personally, I think it is possible, but I'm wondering how you think Husserl understood this in relation to numbers. -
 frank
19kOur basic experience, the most basic one possible (and this will prove to be crucial), is already theory-laden. — J
frank
19kOur basic experience, the most basic one possible (and this will prove to be crucial), is already theory-laden. — J
Right, if we focus heavily on the ontology of abstract objects, we overlook the accompanying problem: what's the basis of our confidence in the other two categories: mental and concrete? It's all myth building. -
 Joshs
6.7k
Joshs
6.7k
So the question I'm posing is whether the "concrete data" are pre-theoretical, which Wang thinks is not possible. Personally, I think it is possible, but I'm wondering how you think Husserl understood this in relation to numbers — J
I believe Husserl argues that all perception is conceptually driven. What appears as concrete data of experience are themselves given relative to modes of givenness constituted by a subject.
“Certainly the world that is in being for me, the world about which I have always had ideas and spoken about meaningfully, has meaning and is accepted as valid by me because of my own apperceptive performances because of these experiences that run their course and are combined precisely in those performances—as well as other functions of consciousness, such as thinking. But is it not a piece of foolishness to suppose that world has being because of some performance of mine? Clearly, I must make my formulation more precise. In my Ego there is formed, from out of the proper sources of transcendental passivity and activity, my “representation of the world, ” my “picture of the world, ” whereas outside of me, naturally enough, there is the world itself. But is this really a good way of putting it? Does this talk about outer and inner, if it makes any sense at all, receive its meaning from anywhere else than from my formation and my preservation of meaning? Should I forget that the totality of everything that I can ever think of as in being resides within the universal realm of consciousness, within my realm, that of the Ego, and indeed within what is for me real or possible?” (Phenomenology and Anthropology)
The question now is whether a thing, which indeed remains one thing under all circumstances, is the identical something of properties and is actually in itself solid and fixed with respect to its real properties; that is, is a thing an identity, an identical subject of identical properties, the changing element being only its states and circumstances? Would this not then mean that according to the various circumstances into which it can be brought, or into which it can be thought to be introduced, the thing has different actual states, but that in advance-a priori - how it can behave, and, further, how it will behave, is predelineated by its own essence?
But does each thing (or, what is equivalent here: does any thing at all) have such an essence of its own in the first place? Or is the thing, as it were, always underway, not at all graspable therefore in pure Objectivity, but rather, in virtue of its relation to subjectivity, in principle only a relatively identical something, which does not have its essence in advance or graspable once and for all, but instead has an open essence, one that can always take on new properties according to the constitutive circumstances of givenness? But this is precisely the problem, to determine more exactly the sense of this openness, as regards, specifically, the "Objectivity" of natural science.”(Husserl, Ideas II) -
 J
2.4k
J
2.4k
But does each thing (or, what is equivalent here: does any thing at all) have such an essence of its own in the first place? Or is the thing, as it were, always underway...?
Husserl's answer seems be that there is no such essence, and each "thing" is indeed always underway (a nice phrase) as a phenomenon to/for our consciousness. I'm wondering, though, whether trying to invoke an essence somewhat prejudices the discussion. My question concerning numbers, for instance, wasn't about whether there was some "essence" of number that is pre-theoretical for us. The question was much more ordinary: What are the concrete contents or data of which Husserl speaks, that allow us to form our idealization of numbers? Can you give an example of how this might work? -
 frank
19k
frank
19k
Maybe like this? This is probably what a Babylonian (500 BC) abacus looked like. This is where the number zero entered into the human intellectual scene. It was when a merchant would draw a diagram of a certain abacus result that he or she would need a symbol for the blank spots. Zero was born as a symbol: an attempt to stop that which underway and record it for future reference. Phenomenologically, it's like when we say we were arrested by the beauty of the sky. Stopping, exiting time, inhabiting an inner sanctum.

-
 Michael
16.8k
Michael
16.8k
Different people may mean different things by "exist" but I don't think different people mean different things by "mathematical platonism", else there wouldn't be much sense in discussing which of platonism, formalism, intuitionism, fictionalism, nominalism, etc. are correct.
My claim is that it doesn't make sense to argue that both of these are true:
1. Quine atoms exist in the platonistic sense
2. Quine atoms don't exist in the platonistic sense
One of them is true and one of them is false. However, regardless of which of (1) and (2) is true, both of these are true:
3. Quine atoms exist according to New Foundations
4. Quine atoms don't exist according to ZFC
And notice the difference between saying that Quine atoms exist according to New Foundations and saying that New Foundations is correct to claim that Quine atoms exist.
Mathematical fictionalists claim that (1) is false and that (2), (3), and (4) are true.
Perhaps a more helpful phrasing of (3) and (4) is this:
3. There is a set that contains only itself according to New Foundations
4. There is not a set that contains only itself according to ZFC -
 J
2.4kMy claim is that it doesn't make sense to argue that both of these are true:
J
2.4kMy claim is that it doesn't make sense to argue that both of these are true:
1. Quine atoms exist in the platonistic sense
2. Quine atoms don't exist in the platonistic sense
One of them is true and one of them is false. — Michael
Is it likewise not sensible to argue that both of these are true?:
1. Sherlock Holmes exists.
2. Sherlock Holmes doesn't exist.
There is more than one way to construe 'exist' here, as I'm sure you'd agree. 1 & 2 can't both be true with the same construal, but that doesn't mean there is no genuine argument about it.
What you're wanting to say is that there is only one way to construe 'exist in the platonistic sense'. As evidence for this, you cite the ongoing disagreements among platonists, nominalists, etc -- they wouldn't make sense, or be to the purpose, without consensus on 'exists'. Indeed! -- and that may be the very problem. What I've tried to argue is that there is another way to understand what these disagreements are about, and why they are so intractable. It may be down to these different construals of 'exist platonically'.
In short, it isn't obvious that mathematical platonism necessitates a commitment to only one construal (one use of ∃) of what it means to exist.
Welcome to The Philosophy Forum!
Get involved in philosophical discussions about knowledge, truth, language, consciousness, science, politics, religion, logic and mathematics, art, history, and lots more. No ads, no clutter, and very little agreement — just fascinating conversations.
Categories
- Guest category
- Phil. Writing Challenge - June 2025
- The Lounge
- General Philosophy
- Metaphysics & Epistemology
- Philosophy of Mind
- Ethics
- Political Philosophy
- Philosophy of Art
- Logic & Philosophy of Mathematics
- Philosophy of Religion
- Philosophy of Science
- Philosophy of Language
- Interesting Stuff
- Politics and Current Affairs
- Humanities and Social Sciences
- Science and Technology
- Non-English Discussion
- German Discussion
- Spanish Discussion
- Learning Centre
- Resources
- Books and Papers
- Reading groups
- Questions
- Guest Speakers
- David Pearce
- Massimo Pigliucci
- Debates
- Debate Proposals
- Debate Discussion
- Feedback
- Article submissions
- About TPF
- Help
More Discussions
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum













