-
 Michael
16.6kI've already stated my argument, and given an example. If I have evidence that I have hazel eyes then I have evidence that "I have hazel eyes or unenlightened has brown eyes" is true. If you can't accept this then I think you have a problem.
Michael
16.6kI've already stated my argument, and given an example. If I have evidence that I have hazel eyes then I have evidence that "I have hazel eyes or unenlightened has brown eyes" is true. If you can't accept this then I think you have a problem. -
 unenlightened
10kI've already stated my argument — Michael
unenlightened
10kI've already stated my argument — Michael
But your argument is invalid.
Let me give you a clue. The premise that you need is something like this:
If p is true then p ∨ q is true.
If there is strong evidence that p is true, then p is true.
Therefore, if there is strong evidence that p is true then there is strong evidence that p ∨ q is true.
Unfortunately, the premise that you need is not true, even according to Gettier. -
 Michael
16.6kLet me give you a clue. The premise that you need is something like this:
Michael
16.6kLet me give you a clue. The premise that you need is something like this:
If p is true then p ∨ q is true.
If there is strong evidence that p is true, then p is true.
Therefore, if there is strong evidence that p is true then there is strong evidence that p ∨ q is true.
Unfortunately, the premise that you need is not true, even according to Gettier. — unenlightened
That's not my argument. And I don't understand what that second premise is doing. -
 unenlightened
10kThat's not my argument. And I don't understand what that second premise is doing. — Michael
unenlightened
10kThat's not my argument. And I don't understand what that second premise is doing. — Michael
Apart from the second premise, it is an exact quote of your argument. The second premise is the hidden premise that would make your argument valid. -
 Michael
16.6kBut your argument is invalid. — unenlightened
Michael
16.6kBut your argument is invalid. — unenlightened
Then let's make it clearer for you by making the principle of closure explicit.
Evidence is closed under disjunction introduction.
"I have hazel eyes" entails by disjunction introduction "I have hazel eyes or unenlightened has brown eyes".
Therefore, strong evidence that "I have hazel eyes" is true is strong evidence that "I have hazel eyes or unenlightened has brown eyes" is true. -
 Michael
16.6kApart from the second premise, it is an exact quote of your argument. — unenlightened
Michael
16.6kApart from the second premise, it is an exact quote of your argument. — unenlightened
Adding to my argument changes my argument. I don't accept that second premise.
The second premise is the hidden premise that would make your argument valid. — unenlightened
I don't need that second premise. -
 unenlightened
10kEvidence is closed under disjunction introduction. — Michael
unenlightened
10kEvidence is closed under disjunction introduction. — Michael
I take this to mean, for our purposes, that what works for truth also works for evidence.
Ok. Now you need to argue that, because that is what we are disputing. You still haven't presented a valid argument.
Adding to my argument changes my argument. I don't accept that second premise. — Michael
Yes, I am charitably making your invalid argument valid. You need another premise of some sort.
I will simply assert that evidence that I have hazel eyes is evidence that "I have hazel eyes or unenlightened has brown" is true. I think it would be absurd to deny this. — Michael
Cool. then we have no argument; you are pontificating, and I am absurd. Have fun. -
 Michael
16.6kCool. then we have no argument; you are pontificating, and I am absurd. Have fun. — unenlightened
Michael
16.6kCool. then we have no argument; you are pontificating, and I am absurd. Have fun. — unenlightened
It's hardly pontificating. It's stating a simple fact that to have evidence that p ∨ q is true is to have evidence that p is true, to have evidence that q is true, or to have evidence that both p and q are true.
So pooh-pooh with a "have fun" all you like. I'm content with my reasonable (and correct) account. -
 unenlightened
10kSo pooh-pooh with a "have fun" all you like. I'm content with my reasonable (and correct) account. — Michael
unenlightened
10kSo pooh-pooh with a "have fun" all you like. I'm content with my reasonable (and correct) account. — Michael
There is nothing I want to say to cause you any discontent. Perish the thought! -
 Srap Tasmaner
5.2kIf p is true then p ∨ q is true.
Srap Tasmaner
5.2kIf p is true then p ∨ q is true.
If there is strong evidence that p is true, then p is true.
Therefore, if there is strong evidence that p is true then there is strong evidence that p ∨ q is true. — unenlightened
We don't have to do it this way.
I didn't bother with conditional probabilities before, but it's the natural way to model Smith's belief.
If is Jones owning a Ford, and is the evidence Smith is relying on, then the belief he holds highly probable is not really just but , the probability of given . And it's dead easy to show that for any
. -
 Srap Tasmaner
5.2kIf p is true then p ∨ q is true.
Srap Tasmaner
5.2kIf p is true then p ∨ q is true.
If there is strong evidence that p is true, then p is true.
Therefore, if there is strong evidence that p is true then there is strong evidence that p ∨ q is true. — unenlightened
Besides which, shouldn't your conclusion be "If there is strong evidence that p, then p v q"? -
 unenlightened
10kIf J is Jones owning a Ford, and D is the evidence Smith is relying on, then the belief he holds highly probable is not really just J but J∣D, the probability of J given D. And it's dead easy to show that for any X
unenlightened
10kIf J is Jones owning a Ford, and D is the evidence Smith is relying on, then the belief he holds highly probable is not really just J but J∣D, the probability of J given D. And it's dead easy to show that for any X
P(J∨X∣D)≥P(J∣D). — Srap Tasmaner
Yes, it's like betting on the favourite and buying a lottery ticket.
It works equally well if one is betting against the favourite.
P(~J∨X∣D)≥P(J∣D).
The more random shit you believe, the more likely you are to be right about something or other. But this does not amount to a system I would be prepared to try at the casino, or a justification for believing random shit.
It's not my conclusion, it's Michael's. I only provided the middle premise, to illustrate that his argument needed one.shouldn't your conclusion be "If there is strong evidence that p, then p v q"? — Srap Tasmaner
If p is true then p ∨ q is true. Therefore, if there is strong evidence that p is true then there is strong evidence that p ∨ q is true. — Michael -
 Cabbage Farmer
301Once you've tested it with the numbers you can substitute back in the ordinary terms: — Michael
Cabbage Farmer
301Once you've tested it with the numbers you can substitute back in the ordinary terms: — Michael
It seems we're in agreement on the underlying logic. -
creativesoul
12.2kWhen the criterion for being true is satisfied by being the result of a valid inference, it is prima facie evidence of an inadequate conceptual scheme hard at work. Patent falsehood can be the result of a valid inference. If being the result of a valid inference counts as being true, then patent falsehoods are true. These examples are too numerous to deny. Truth cannot be false. It only follows that validity alone is insufficient for truth; validity alone does not guarantee truth; validity alone does not necessarily transmit and/or transport truth through it's form; validity alone is found wanting, needing, lacking, and begging for truth. Our knowing that much also allows us to know that being the result of a valid inference alone constitutes neither being well-grounded nor true.
The primary operator in all thought/belief and the formation thereof is the presupposition of correspondence with/to: fact; reality; the case at hand; the way things are/were; the universe; etc.(correspondence henceforth). At the moment of conception, all agents capable of drawing associations/correlations/connections between 'objects' of physiological sensory perception are completely void thereof. Thought/belief - like knowledge - is accrued. As such, it begins with simple/basic/rudimentary associations/correlations drawn between 'objects' of physiological sensory perception and/or the agents 'own' state of mind, and it grows in it's complexity. Initial thought/belief formation instantiates the presupposition of truth and the attribution of meaning inherent to all thought/belief and statements thereof.
Thought/belief is prior language. Correspondence to fact/reality is presupposed within thought/belief formation long before language acquisition has begun in earnest. Correspondence is presupposed prior language, because association/correlation presupposes the existence of it's own content. Some of those associations/correlations correspond to fact/reality. True thought/belief is prior to language. So, either truth exists without language, or true thought/belief exists without truth.
Being the result of a valid inference is existentially contingent upon language. Correspondence is not. The former does not constitute the latter. Our knowing that much also allows us to know that being the result of a valid inference alone does not necessarily constitute being either well-grounded or true. In addition, it only follows that validity is existentially contingent upon the presupposition of correspondence and the attribution of meaning, including but not limited to the recognition/attribution of causality.
Smith's accepts all three disjunctions based upon his well-grounded belief that Jones owns a Ford, if we adhere strictly to Gettier's account of Smith's reasoning for accepting the disjunctions based upon that belief. Smith is purportedly 'justified in believing' all three propositions because he believes Jones owns a Ford and recognizes the entailment of each of the three 'propositions'.
Here, it is crucial to note that Smith holds more than one belief about the disjunctions. He believes that they follow the rules of correct inference. That belief is true. He believes that all three are true if, and only if, the truth conditions are met. That belief is true. He believes that all three are true because Jones owns a Ford. That is the part left out by those who report upon Smith's belief, even when the reporter includes this crucial step when reporting upon their own thought/belief. Believing a disjunction requires precisely the process I've outlined. A proper account of believing a disjunction has been offered. There are no problems with it, and no disjunction is immune. None. Here it is again...
p1. ((p) is true)
p2. ((p v q) follows from (p))
p3. ((p v q) is true if...(insert belief statement(s) regarding what makes this particular disjunction true))
C1. ((p v q) is true because... (insert belief statement(s) corresponding to the prior 'if'))
That is what believing a disjunction consists in/of. I've invited anyone to imagine a disjunction arrived at by a rational agent on the basis of believing P that is not completely exhausted by the above solution. There are no problems. Fill it out. -
 Srap Tasmaner
5.2kP(~J∨X∣D)≥P(J∣D). — unenlightened
Srap Tasmaner
5.2kP(~J∨X∣D)≥P(J∣D). — unenlightened
Not sure why you think this.
Here's a diagram for what I said, which was :

That seems pretty straightforward: we start with the yellow and green bits and pick up the blue as well. The blue might be empty, but we still know yellow+green+blue ≥ yellow+green.
Now here's yours, which was :
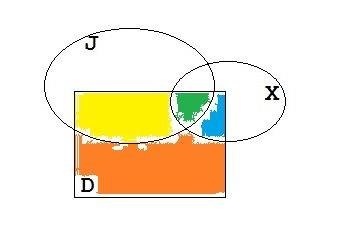
Your claim is that orange+blue+green≥yellow+green. Maybe, maybe not. Depends on whether orange+blue≥yellow, doesn't it? And our hypothesis was that yellow+green is pretty big: Smith has strong evidence for his belief.
Two more points. Another interpretation of Smith's belief would be:
which looks like this:

That adds in the light blue bit. I don't think there's any reason to do this though, because all of Smith's reasoning is relative to , his reasons for believing Jones owns a Ford. Adding the light blue bit doesn't change the argument anyway. It's just a bigger version of the "≥" we've already got.
Now what about ? Are the reasons Smith has for believing Jones owns a Ford reasons to believe Brown is in Barcelona? Well, they're not reasons to believe he isn't: there's no reason to think that Jones having always owned a car and always a Ford and now driving a Ford, etc., precludes Brown from being in Barcelona. So there's no reason to think and are disjoint. But it doesn't give you much to go on, so when I assigned a prior to , I made it tiny, and that seems reasonable to me.
((Apologies for the crumminess of the diagrams.)) -
creativesoul
12.2kCertainty is a measure of conviction and it is proportional to i. the sheer number of thought/belief grounded upon that which one is certain of, probability notwithstanding, and/or ii. the sheer number of times that the belief has been reaffirmed.
Gettier is certain that he has made a case of Smith having justified true belief that ought not count as knowledge. His certainty is grounded upon the idea that believing a disjunction does not need to include the agents' believing that it's true because the truth conditions have been met. His certainty is based upon a partial account of believing a disjunction. When an account of believing a disjunction neglects the steps necessary for how one arrives at such a belief, it is an inadequate account. When such neglect changes the very meaning of the belief itself, the result is something other than the actual belief that is supposed to be under scrutiny. If the alternative is true, but the actual belief is false, then...
Bewitchment. Self-induced by inadequate language use. -
 Srap Tasmaner
5.2kCan we make anything out of the difference between, on the one hand, A being a reason for believing B, and, on the other, A merely ("merely"?) being consistent with B?
Srap Tasmaner
5.2kCan we make anything out of the difference between, on the one hand, A being a reason for believing B, and, on the other, A merely ("merely"?) being consistent with B? -
creativesoul
12.2kI think that there is something to be gleaned out of the fact that B consists of more than one statement. What counts as being a proposition is starkly different than what counts as being a belief statement. -
creativesoul
12.2kThe statement "the man who has ten coins in his pocket will get the job" is true because Jones will get the job, and Jones has tens coins in his pocket.
That is Smith's belief.
It doesn't talk about the rules... it follows them. Our talk about Smith's belief ought include not only applying the rules to it, but also showing that Smith's belief has been arrived at by virtue of following them. That requires including the ground. Leaving that out is akin to removing the ground necessary not only for Smith's arriving at the believing that statement, but also for our adequately accounting of it. -
creativesoul
12.2kSmith is justified in his false belief. Gettier is not justified in leaving out the necessary content thereof. -
 Srap Tasmaner
5.2kI think that there is something to be gleaned out of the fact that B consists of more than one statement. What counts as being a proposition is starkly different than what counts as being a belief statement. — creativesoul
Srap Tasmaner
5.2kI think that there is something to be gleaned out of the fact that B consists of more than one statement. What counts as being a proposition is starkly different than what counts as being a belief statement. — creativesoul
Yeah, that's an option.
Conjunctions would be easy, I guess-- just two beliefs instead of three. And you could work up an approach that doesn't treat disjunctions, conditionals, counterfactuals as being potential truth-bearers at all. (Just inference rules or habits.) What about negatives?!
It's worth playing around with. -
creativesoul
12.2kSince you mentioned it...
The truth-bearing approach works from the historical and quite mistaken presupposition that truth is existentially contingent upon language. It also claims that statements(etc.) are true solely by virtue of expressing a true proposition. That unnecessarily multiplies the level of difficulty inherent to taking proper account of what sorts of things can be true/false and what makes them so. We're still left with the same set of questions, and we've overcomplicated the pursuit.
In addition, any and all positions that work from the presupposition that truth requires language cannot admit of true/false pre-linguistic and/or non-linguistic thought/belief despite everyday happenings/events bearing witness to the brute fact that they are being continuously formed and held prior to language. Language creation requires pre-existing thought/belief. Language discovery requires the same. Language acquisition requires the same. Formal language requires natural. Natural requires thought/belief. Thought/belief presupposes it's own correspondence to fact/reality, as do belief statements. Propositions do not. Why continue using frameworks that do not take this into proper account?
It makes no sense whatsoever to posit that Smith's belief consists of that which he does not believe.
That's what Gettier proposes by claiming that Smith is completely justified in believing (g), (h), and (i). That, in and of itself, either renders the notion of belief incoherent and/or unintelligible, or it is prima facie evidence that Gettier works from an utterly inadequate notion thereof.
Neither is acceptable.
Propositions are not equivalent to belief statements. -
creativesoul
12.2kSmith's simultaneously believing all three of the following disjunctions is impossible unless Smith has no belief regarding Brown's whereabouts, and it is possible to believe that a disjunction is true even if it contains a proposition which is not believed. The rules say that that's possible, and it is.
"Either Jones owns a Ford, or Brown is in Boston."
"Either Jones owns a Ford, or Brown is in Barcelona."
"Either Jones owns a Ford, or Brown is in Brest-Litovsk."
Smith has no belief regarding Brown's whereabouts. And yet, for half a century, everyone has ignored the fact that Gettier claims that Smith's belief consists of that which he does not believe. During the same timeframe, everyone has agreed with Gettier that Smith's belief is true solely by virtue of where Brown is located even though Smith holds no belief regarding Brown's whereabouts.
That's impossible. Smith does not believe that Brown is in Barcelona, so Brown's being in Barcelona cannot make Smith's belief true.
Here's where a defender of Gettier will invoke the rules of disjunction. One can believe a disjunction is true if s/he believes that one, the other, or both are true. I would agree and demand that Smith's belief be adequately accounted for. Particularly, our account of Smith's belief ought not claim that it contains something that he does not believe. The disjunctions, as written above, contain a statement that Smith does not believe. Granted, they are part of the disjunctions, and Smith does believe the disjunctions are true. It is clear that our account of Smith's believing the disjunctions ought reflect the fact that Smith does not believe anything at all about Brown's whereabouts. Gettier says as much in his narrative, and yet neglects to adequately represent what Smith does believe.
Smith believes that all three disjunctions are true because Jones owns a Ford.
One of the disjunctions is true, because Brown is in Barcelona.
Smith holds false belief. -
creativesoul
12.2kI mean... C'mon people.
What sense does it make to offer an account of belief which contains that which is not believed?
None.
Sure, a disjunction can contain a statement which is not believed, and it does in the case of Smith. However, since that is the case, and Smith does not believe the statement, then our account of Smith's belief ought reflect that fact.
Smith believes that all three disjunctions are true because Jones owns a Ford. -
creativesoul
12.2kIn the end, I'm not even questioning the rules of disjunction. I'm showing that believing a proposition is not always adequately accounted for by virtue of showing only the proposition. This is particularly the case when and if one introduces a disjunction and/or any other kind of compound or complex statement of thought/belief. I'm also showing that belief is not equivalent to a conclusion, no matter how it is arrived at. Propositions are not equivalent to belief. Statements are not necessarily statements of one's belief either.
One can state something that they do not believe. One can construct disjunctions that contain statements that one does not believe. Gettier had Smith do just that, and he had Smith deliberately misrepresent his own thought/belief in the process. Gettier posited this situation for rhetorical effect, and it worked.
Think about what happens when one states something that s/he does not believe. Just for argument's sake, would we claim that they have true belief if what they claimed were true, despite the fact that they did not believe it when uttering it?
Of course not.
It's all about belief. Justified. True. Belief.
I suggest that we learn to correct our accounting errors. -
creativesoul
12.2kIf there are good reasons to believe p then there are good reasons to believe p ∨ q. How could it be any other way?
This presupposes belief that p or q is true if p is true.
Welcome to The Philosophy Forum!
Get involved in philosophical discussions about knowledge, truth, language, consciousness, science, politics, religion, logic and mathematics, art, history, and lots more. No ads, no clutter, and very little agreement — just fascinating conversations.
Categories
- Guest category
- Phil. Writing Challenge - June 2025
- The Lounge
- General Philosophy
- Metaphysics & Epistemology
- Philosophy of Mind
- Ethics
- Political Philosophy
- Philosophy of Art
- Logic & Philosophy of Mathematics
- Philosophy of Religion
- Philosophy of Science
- Philosophy of Language
- Interesting Stuff
- Politics and Current Affairs
- Humanities and Social Sciences
- Science and Technology
- Non-English Discussion
- German Discussion
- Spanish Discussion
- Learning Centre
- Resources
- Books and Papers
- Reading groups
- Questions
- Guest Speakers
- David Pearce
- Massimo Pigliucci
- Debates
- Debate Proposals
- Debate Discussion
- Feedback
- Article submissions
- About TPF
- Help
More Discussions
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum






