-
 Moliere
6.5kYes! :D Reading him reminds me of an old math prof I had, actually -- his mind was so intuitively mathematical that what seemed like not worth mentioning to him was something that was crucially important for me to follow his reasoning.
Moliere
6.5kYes! :D Reading him reminds me of an old math prof I had, actually -- his mind was so intuitively mathematical that what seemed like not worth mentioning to him was something that was crucially important for me to follow his reasoning.
I'm not giving up or anything. It's just taking time. -
 fdrake
7.2k
fdrake
7.2k
I'm finding the same thing, what I'm benefitting most from I think is trying to integrate the imaginative background from the first section with the mechanical mathsy bits in the second. I imagine philosophically the first section and the final section would do, so if others feel like this isn't progressing quick enough to the philosophical juicy bits I could summarise the maths so far and then we could move on to §3. -
 unenlightened
10kDoing my best to remain silent so's not to remove all doubt, but thought y'all might like some dimensional confusion. Why read, when you can play?
unenlightened
10kDoing my best to remain silent so's not to remove all doubt, but thought y'all might like some dimensional confusion. Why read, when you can play?
https://www.youtube.com/watch?v=lX5eCfRSCKY -
 Moliere
6.5kTo find the simplest cases, I shall seek first an expression for manifoldnesses of n - 1 dimensions which are everywhere equidistant from the origin of the linear element; that is, I shall seek a continuous function of position whose values distinguish them from one another. In going outwards from the origin, this must either increase in all directions or decrease in all directions; I assume that it increases in all directions, and therefore has a minimum at that point. If, then, the first and second differential coefficients of this function are finite, its first differential must vanish, and the second differential cannot become negative; I assume that it is always positive. This differential expression, of the second order remains constant when ds remains constant, and increases in the duplicate ratio when the dx, and therefore also ds, increase in the same ratio; it must therefore be ds2 multiplied by a constant, and consequently ds is the square root of an always positive integral homogeneous function of the second order of the quantities dx, in which the coefficients are continuous functions of the quantities x.
Moliere
6.5kTo find the simplest cases, I shall seek first an expression for manifoldnesses of n - 1 dimensions which are everywhere equidistant from the origin of the linear element; that is, I shall seek a continuous function of position whose values distinguish them from one another. In going outwards from the origin, this must either increase in all directions or decrease in all directions; I assume that it increases in all directions, and therefore has a minimum at that point. If, then, the first and second differential coefficients of this function are finite, its first differential must vanish, and the second differential cannot become negative; I assume that it is always positive. This differential expression, of the second order remains constant when ds remains constant, and increases in the duplicate ratio when the dx, and therefore also ds, increase in the same ratio; it must therefore be ds2 multiplied by a constant, and consequently ds is the square root of an always positive integral homogeneous function of the second order of the quantities dx, in which the coefficients are continuous functions of the quantities x.
Alright, I have a question about this. I thought I was following until the end here.
As I understand it what Reimann is saying is that the displacement of a line does not alter the length of the line -- it's not like the coordinates themselves follow some kind of progression where the space between 1 and 2 is smaller than the space between 3 and 4. The space is equidistant.
In the quoted bit it seemed to me that he was considering a manifold which is a straight line (segment?), and he is trying to establish the rate of change of x with respect to s (or vice versa?). But then I get lost when he is using the 2nd derivative, because by my figuring that would be equal to zero since he was considering a straight line? -
 JimRoo
12My understanding is when Riemann is talking about the 2nd derivative, he is talking about the 2nd derivative of the metric function, the function for ds:
JimRoo
12My understanding is when Riemann is talking about the 2nd derivative, he is talking about the 2nd derivative of the metric function, the function for ds:
ds is the square root of an always positive integral homogeneous function of the second order of the quantities dx
He uses the example of this function in Space:
-
 fdrake
7.2kThis isn't from the paper, it uses mostly external ideas to what's been presented in the paper so far.
fdrake
7.2kThis isn't from the paper, it uses mostly external ideas to what's been presented in the paper so far.
If I can make an analogy, imagine yourself as a point rolling down a hill. When the hill changes shape, so does your acceleration. A 'straight line' on the surface of the hill isn't a 'straight line' in the embedding space. To be sure, if we have that the manifold is locally flat, 'straight lines' of tiny extent on the manifold will look like straight lines in a Euclidean embedding space. But they don't actually have to be straight (in the sense of the embedding space) because of the possibility of curvature.
Though, I think some of your intuition about the derivative is correct. Imagine if we place two points A, B on the hill really close together and draw a smooth path between them, like a piece of string bound tightly to the surface.
A-----B
Imagine that we parametrise this path so that s=0 at point A and s=k at point B - this uniquely specifies every point on the path. The average change in the function (per unit length on the path) that this path corresponds to would be:
so the second derivative would be 0, since the first would be a constant (except if the points A and B coincided). But what does this calculation actually mean? All the function f does is take the arclength along the curve between A and B and spit it back out. IE f(s)=s, with f(A)=0 and f(B)=k. The rate of change of the arclength with respect to itself is always 1. More generally, the rate of change of any function with respect to itself is always 1.
Another thing to note is that the tangent vector to a manifold at a point - a line that is visualised in the embedding space - agrees with the first derivative of the manifold in its direction, but the second derivative of the tangent vector is 0 - whereas the manifold itself 'curves away' from it, showing the presence of a nonzero second derivative of the manifold (with respect to the coordinate system we're using) - curvature.
The situation that we usually have on the manifold is more like the form:
where there is more than one coordinate required in the specification of the path, if it's a one dimensional curve we also have that y(s) = f(x(s)). This means that we can consider how the curve bends over the coordinate system x(s), y(s). The curve itself, like the length of wiring, can be straightened out, so the curvature it has isn't intrinsic to its shape. This ability to straighten out something precisely means that there is a smooth transformation from distances within the shape to distances like they behave in a Euclidean (flat) space. You can also visualise this as the curvature of spaces rendering the linear approximation to their surface (like the tangent plane or vector) worse and worse when you go away from the point of approximation.
So it might be that we can bend the wire, but we don't introduce any irremovable/intrinsic curvature. What intrinsic curvature actually measures is how movements of oriented objects constrained within the surface change the orientation of those objects when moving around closed paths - paths with the same start and end point.
This even applies to forming a circle out of it, circle boundaries don't have intrinsic curvature whereas the surfaces of spheres do! A tangent vector to a circle at one point, transported around the circle while remaining tangent, is still in the same direction as it was when you started! You can check this by rotating, say, your phone around the top of a coffee mug. So let's talk about the surface of a sphere.
Another task we might imagine is taking a perfectly taut bit of copper wiring and trying to wrap it onto the surface of a sphere. You can press it onto a point, and it'll touch the point. But, if the sphere is absolutely huge relative to the size of the perfectly taut bit of string, the taut bit of wire might resemble the surface of the sphere very well, it wraps away slowly from the wire with respect to spatial changes (points flowing away from the wire). If the sphere is tiny compared to the bit of string, it just glances off it and the sphere quickly wraps away from it. The acceleration with which the sphere wraps away from the taut bit of string is its curvature (no acceleration = flat!) - in the small sphere case you'd have to bend the wire a lot to fit the surface, in the large sphere case you'd have to bend the wire a tiny amount to fit the surface. The curvature of the surface of a sphere is not something that can be removed by these smooth transformations.
The presence of curvature, like on the surface of a sphere, does something pretty strange to straight lines from the embedding space. If you take the iron wire, press it onto a point on the surface of the sphere, and you hold it onto the sphere, what happens when you take the iron wire, still taut and straight, from around a closed path on the sphere? This requirement that it's still tight equates to that the iron wire must be tangent to the sphere. If you move it along a path, where the start and end points of the path are the same (say carving out a quarter of the sphere). By the time it's back to its start, the direction you're holding the iron wire in actually changes. The presence of these changes signals intrinsic curvature.
You can check this with your fist and your mobile phone. Clench your fist with your thumb toward you, take your phone and press it hard onto the knuckle of your index finger. Push the phone away from your body along the line of your knuckles. When it gets past your final knuckle, still keeping it pressed onto your hand, force the phone towards you from the first finger joint on your pinky to the first finger joint on your index finger. Finally, bring it back from the first joint on your index finger to the base of your thumb, and back up again to the first knuckle. You should see that the phone has inverted. Contrast this to the mug and phone thing from earlier. -
 SapereAude
19I have been a bit busy lately and have just now taken a look at the essay. Is there someone who can give me some background on the work: Why is it important? Who wrote it? Historical background? Philosophical background?
SapereAude
19I have been a bit busy lately and have just now taken a look at the essay. Is there someone who can give me some background on the work: Why is it important? Who wrote it? Historical background? Philosophical background? -
 fdrake
7.2k
fdrake
7.2k -
 Streetlight
9.1k@fdrake”: "Aw man, behind on this and §3 (of section I!) is really killing me, even with your exposition. I get that the overall aim here is to show how to ‘decompose’ a manifoldness, but I don’t quite understand the demonstration he sets up to explain it. Two questions to begin with:
Streetlight
9.1k@fdrake”: "Aw man, behind on this and §3 (of section I!) is really killing me, even with your exposition. I get that the overall aim here is to show how to ‘decompose’ a manifoldness, but I don’t quite understand the demonstration he sets up to explain it. Two questions to begin with:
(1) “Let us suppose a variable piece of a manifoldness of one dimension” - I’m not sure what work the word ‘variable’ does here in ‘variable piece of a manifoldness’. Can one take an invariable piece of a manifold? And what would this distinction mean?
(2) “Let us take a continuous function of position within the given manifoldness, which, moreover, is not constant throughout any part of that manifoldness.” - Here, I’m not sure what work ‘not constant’ is doing. Is it the variation of position on the manifoldness we are asked to think of is ‘not constant’?
I don’t think I can work my way through the rest of the paragraph without getting these fundamentals down. -
 fdrake
7.2k(1) “Let us suppose a variable piece of a manifoldness of one dimension” - I’m not sure what work the word ‘variable’ does here in ‘variable piece of a manifoldness’. Can one take an invariable piece of a manifold? And what would this distinction mean? — StreetlightX
fdrake
7.2k(1) “Let us suppose a variable piece of a manifoldness of one dimension” - I’m not sure what work the word ‘variable’ does here in ‘variable piece of a manifoldness’. Can one take an invariable piece of a manifold? And what would this distinction mean? — StreetlightX
I read that as saying variable piece of a manifoldness might be a connected chunk of a manifoldness. But when we take 'a' variable piece of a manifoldness Riemann intends us to be discussing an arbitrary one. The other bit 'of one dimension', connotes that the manifoldness he's considering is just a 1 dimensional curve.
So you might imagine cutting a cylinder down the middle really finely to produce a circle.
(2) “Let us take a continuous function of position within the given manifoldness, which, moreover, is not constant throughout any part of that manifoldness.” - Here, I’m not sure what work ‘not constant’ is doing. Is it the variation of position on the manifoldness we are asked to think of is ‘not constant’? — StreetlightX
This continuous function describes what point you are on on the previously considered curve. If the function was something like f(x)=x for x<1 and f(x)=1 for all x>=1, this makes the entire region [1,infinity) map to 1, so it can't be used to uniquely specify the position. More specifically, in this example, if you know the function is f(x) = x, you can take an output of this function f(x) and directly map it to an input x, allowing you to translate between the position described using the function and the position on the manifold. However, when this x becomes greater than 1, all this function tells you is that it's equal to 1. Which means the input which caused the function to be 1 could be anywhere between 1 and infinity - so we can't invert the function to uniquely specify the point on the curve. -
 fdrake
7.2kRight, so I finally have some purchase on the construction in section 2 §2. This post will be heavily edited to include diagrams later. Anyone more experienced with math in this field please correct me.
fdrake
7.2kRight, so I finally have some purchase on the construction in section 2 §2. This post will be heavily edited to include diagrams later. Anyone more experienced with math in this field please correct me.
Imagine we're on the surface of a wibbly wobbly sphere, and we pick a point O and call it the origin. We're going to look at the distance from O to nearby points.
For this purpose let us imagine that from any given point the system of shortest limes going out from it is constructed; the position of an arbitrary point may then be determined by the initial direction of the geodesic in which it lies, and by its distance measured along that line from the origin.
From O, we move out in every direction along the shortest possible path. We can imagine this as inscribing a wibbly wobbly circle on the wibbly wobbly sphere and drawing lines on it which hug the surface and are as straight as possible.
We then pick another point on the wibbly wobbly sphere within the wibbly wobbly circle. Since we drew the 'system of shortest lines (geodesics)', and drew all of them, this point will lay on one of the geodesics. Therefore, we can relate the position of this point to its position on the geodesic. In order to do this, we need to look at how the geodesic hugs the sphere - which means we need to look at how the geodesic changes over the wibbly wobbly circle within the wibbly wobbly sphere. That is, we need to relate the new point to the old point using the geodesic line and the coordinate system the wibbly wobbly sphere is in (the embedding space).
Riemann's recipe for this is:
It can therefore be expressed in terms of the ratios dx0 of the quantities dx in this geodesic, and of the length s of this line. Let us introduce now instead of the dx0 linear functions dx of them, such that the initial value of the square of the line-element shall equal the sum of the squares of these expressions, so that the independent varaibles are now the length s and the ratios of the quantities dx. Lastly, take instead of the dx quantities x1, x2, x3,..., xn proportional to them, but such that the sum of their squares = s2
The quantities 'in' the geodesic are the embedding coordinate system quantities which vary with it - like the angle when moving on the boundary of a circle. The ratios are the rates of change of each coordinate with respect to every other. EG, moving around the boundary of a circle, we never change the distance from the origin-we have a fixed radius, so the rate of change with respect to the distance from the origin is 0, whereas the rate of change with respect to the angle from the horizontal axis is 1. IE we are looking at and , the being the distance of the point in the embedding space from the origin and the angle of rotation from the positive x-axis , rotating clockwise around the boundary of the circle by moves with respect to changes and with respect to . So the distance between two points on the boundary of a circle only increases with respect to the angle (sweeping out an interpoint distance of infinitesimally, and does not increase with respect to the radius since the distance from the origin does not change.
Riemann wants to generalise from this notion, instead of necessarily having two independent coordinates, the system of points going out from the origin might (and in general will) be functions of multiple dimensions from the embedding space - a general interpoint distance on the wibbly wobbly surface depends on changes in all the in the embedding space coordinates. This means instead of just looking at independent sums where , he wants it to be . What this looks like for a curve with inputs from the embedding space that outputs a position on the surface is.
where is a matrix that stores all the at the chosen origin. This interfaces with the y variables through the chain rule:
and stores the results in the vector . This vector can be thought of as a linear displacement from 0 - (edit: like the gradient operator combined with the chain rule), and Riemann then insists that when the displacement is infinitesimally small - when we increment along the curve by , this gives us the square of the line element:
the intuition here is that we need to increment along 'all the quantities in the geodesic', which are the , so that the infinitesimal increment in position becomes:
and the norm of this increment is then
through Pythagoras (and the flat space stuff from before). Which Riemann states as if it is incredibly obvious:
When we introduce these quantities, the square of the line-element is \sum dx^2 for infinitesimal values of the x,
. It should be noted here that the embedding space coordinates are kind of extraneous so long as we are considering increments confined to the surface - IE, whenever we write a y or a dy it's also secretly an x or a dx, and all this chain rule stuff does is express how the changes on the surface coordinates (system of geodesics) work with respect to the embedding coordinates which we initially used to express them. This local linear approximation of changes on the manifold with respect to the embedding space using the variables on the manifold is what Riemann achieves through the proportion construction
. Let us introduce now instead of the dx0 linear functions dx of them, such that the initial value of the square of the line-element shall equal the sum of the squares of these expressions, so that the independent varaibles are now the length s and the ratios of the quantities dx.
by fixing the 'initial value' to be the sum of the squares of the increment's norm. The increment's norm gives us the local linearity, the remaining discussion refines the approximation of to include quadratic terms that express the curvature. -
 fdrake
7.2kFinally a picture of what's going on:
fdrake
7.2kFinally a picture of what's going on:

For the sake of actually moving on in the reading group, I'm going to stop trying to get the math down precisely. The picture here gives the broad-strokes steps Riemann uses to define the curvature in 2§2. 2§3 is much more qualitative - expressing the 'donut is a coffee cup' and 'boundary of a cylinder is a plane' notions in topology. -
 I like sushi
5.3k
I like sushi
5.3k
Badger here! On Nietzsche binge at the moment, but I’m hoping to have a proper go at Logical Investigations soon ... ish! Meaning within next 6 months!
Nietzschewise should be starting On the Geneaology of Morals in a week or so for the first time. Note: I purposely don’t read the translastors intro on the first read so I’ll be completely new to the text. -
 fdrake
7.2k2§3, trying to build momentum again:
fdrake
7.2k2§3, trying to build momentum again:
Riemann abstracts from the analysis of specific surfaces and their coordinate systems to properties which remain the same after the surface has been deformed.
There are two points here: the first is that if you bend a surface, you can account for the bend through a change in coordinate system - you just need to chart where the points started, the initial shape, and where the points ended up; the function which takes you from start to end is a coordinate transformation. The second is that transforming a shape can be thought of as a way of taking the points on it onto other points, a function which maps points to points again.
Constraining the types of function which bend shapes or transform coordinate systems into each other will allow the the study of invariants to those transformations; which are thereby intrinsic properties of the manifold considered.
The methodological move here is to define what is intrinsic to a shape with reference to what does not change when you transform it. This is the idea where the (long ago now) mentioned difference between intensive and extensive types of analysis is partly inspired by.
For a physical analogy, take two balls made entirely of iron, the sizes can differ but the density is the same. Or when you pour water out of your kettle into a cup, the temperature of the water in the cup is the same as the water in the kettle, whereas there's more heat energy in the larger volume. Density and temperature are then intensive properties, volume and heat energy are extensive properties.
Riemann wants to introduce a similar distinction within the study of manifolds; intensive/intrinsic properties are those that do not depend upon any particular coordinate system or object deformation for their expression, extrinsic/extensive properties conversely depend upon a particular coordinate system or object deformation.
He sets this up in the first paragraph of §3.
§ 3. In the idea of surfaces, together with the intrinsic measure-relations in which only the length of lines on the surfaces is considered, there is always mixed up the position of points lying out of the surface. We may, however, abstract from external relations if we consider such deformations as leave unaltered the length of lines - i.e., if we regard the surface as bent in any way without stretching, and treat all surfaces so related to each other as equivalent. Thus, for example, any cylindrical or conical surface counts as equivalent to a plane, since it may be made out of one by mere bending, in which the intrinsic measure-relations remain, and all theorems about a plane - therefore the whole of planimetry - retain their validity. On the other hand they count as essentially different from the sphere, which cannot be changed into a plane without stretching.
The specific constraint he places on deformations to make this distinction between intrinsic and extrinsic properties is that the deformation must preserve the length of lines within the object. In this manner, if you draw two dots on a piece of paper and measure the distance between them with a tape measure, then fold the tape measure and the paper together to make a cylinder, the tape measure will still report the same distance between the two dots after the deformation. The existence of a deformation which can transform one object into another without changing the length of lines within the object; or equivalently the interpoint distances constrained to the object; means that two objects can be treated as equivalent.
Therefore, if you can take a plane and bend it into some other shape, the theorems of plane geometry will continue to apply to it. If you cannot bend a plane into another shape, it will have different intrinsic properties; it will require different geometric laws to model.
This connection between geometry and the intrinsic properties of surfaces is the point in the analysis which suggests that there are a plurality of geometries, rather than simply the geometry of a Euclidean embedding space. Geometries track intrinsic properties of manifolds, and constrain the coordinate systems which can be used to express them; by means of limiting whether an appropriate deformation exists between an object in one configuration and an object in another. Riemann gives the example of the surface of a sphere as a manifold which cannot be appropriately deformed into a plane.
According to our previous investigation the intrinsic measure-relations of a twofold extent in which the line-element may be expressed as the square root of a quadric differential, which is the case with surfaces, are characterised by the total curvature. Now this quantity in the case of surfaces is capable of a visible interpretation, viz., it is the product of the two curvatures of the surface, or multiplied by the area of a small geodesic triangle, it is equal to the spherical excess of the same. The first definition assumes the proposition that the product of the two radii of curvature is unaltered by mere bending; the second, that in the same place the area of a small triangle is proportional to its spherical excess
In one dimension, for curves, the radius of curvature at a point is the radius of a circle tangent to that curve which fits the closest to it; the curvature at that point is then the reciprocal of the radius of curvature. In higher dimensions, tangents are replaced with tangent spaces, the spheres to their higher dimensional analogues, and the point they touch the surface must have the radius normal to the surface.
The 'two curvatures' of a surface (in 3 space) are the directions in which the curvature changes least and most at a point. These depend on the deformation of an object; and so are extrinsic properties.
The idea behind this is to wrap a surface onto a circle or sphere (the Gauss map), you take the radius of curvature and the direction it lays in, then shift the line segment representing the radius to have its origin in the centre of a circle or sphere. You do this for every point on the desired surface, making a function from the surface you're studying to the circle or sphere. Intuitively, the rate of change of this function with respect to displacements on the original surface measures the angular changes in normal vectors with respect to movement on the surface; if the normal vector never changes angle, the shape is a plane. Of course, for higher dimensional manifolds, there will be various directions we can choose for the displacements on the original surface, meaning we need to represent changes in all directions in the same mathematical object. This is done by finding a basis for the directions in which a normal vector can change, then expressing the rate of change in each direction. The two curvatures (for a 3 dimensional surface), then, quantify the amount of curvature change in directions of maximal and minimal curvature change.
The spherical excess is just another way to measure this angular change. Riemann then wants to generalise this construction to an intrinsic feature of the surface; and he does this by defining the above directions of variation in terms of geodesics which stem from a point; the geodesic is uniquely determined by the initial direction it moves away from the point, and these directions are the directions of variation for a normal vector to that point. Thereby, the notion of displacement in the previous paragraph is made intrinsic to the surface by relating the directions of normal vector change to the directions geodesics can travel away from a point.
The previous discussion in 2§2 then applies when we have chosen appropriate geodesics to express variation on the surface. Riemann summarises this by saying that the above geodesic construction determines the curvature. Since the construction was based on the length of lines, it will also be invariant to transformations which preserve length of lines.
To give an intelligible meaning to the curvature of an n-fold extent at a given point and in a given surface-direction through it, we must start from the fact that a geodesic proceeding from a point is entirely determined when its initial direction is given. According to this we obtain a determinate surface if we prolong all the geodesics proceeding from the given point and lying initially in the given surface-direction; this surface has at the given point a definite curvature, which is also the curvature of the n-fold continuum at the given point in the given surface-direction. -
 fdrake
7.2kClarifying note: a basis is a collection of directions which can be used to express an arbitrary displacement. EG, for 2 dimensional space, the plane, 'up' and 'along' work. Every point can be travelled to from any other by moving an amount 'up' and an amount 'along'. Riemann simply changes 'up' and 'along' to the relevant directions on a surface; which, say, for a circle would just be 'rotate clockwise', or the surface of sphere would be 'rotate up' and 'rotate sideways'.
fdrake
7.2kClarifying note: a basis is a collection of directions which can be used to express an arbitrary displacement. EG, for 2 dimensional space, the plane, 'up' and 'along' work. Every point can be travelled to from any other by moving an amount 'up' and an amount 'along'. Riemann simply changes 'up' and 'along' to the relevant directions on a surface; which, say, for a circle would just be 'rotate clockwise', or the surface of sphere would be 'rotate up' and 'rotate sideways'. -
 fdrake
7.2k2§4
fdrake
7.2k2§4
4. Before we make the application to space, some considerations about flat manifoldness in general are necessary; i.e., about those in which the square of the line-element is expressible as a sum of squares of complete differentials.
In a flat n-fold extent the total curvature is zero at all points in every direction; it is sufficient, however (according to the preceding investigation), for the determination of measure-relations, to know that at each point the curvature is zero in ½ n (n - 1) independent surface directions.
This follows from the previous discussion; it's enough to know the curvature is zero in a subset of independent surface directions to know it's zero in all of them. Riemann then generalises the discussion from surfaces of 0 curvature to surfaces of constant curvature (0 is a constant).
Manifoldnesses whose curvature is constantly zero may be treated as a special case of those whose curvature is constant. The common character of those continua whose curvature is constant may be also expressed thus, that figures may be viewed in them without stretching.
If we have a rubber sheet and roll it into a cylinder, interpoint distances don't change; this follows from thehe thought experiment with the measuring tape pinned to the surface). If you stretch the rubber sheet, then the measuring tape would have to stretch too to mark the new interpoint distance. This follows through contraposition (P=>Q <=> ~Q => ~P), where 'Q' is 'curvature is constant' and 'P' is 'figures may be viewed in them by stretching'. It's easier to imagine ~Q, where the curvature changes - which means the measuring tape would have to stretch to fit snugly to the object -, which would therefore mean the figures inscribed on the surface would have their interpoint distances changed too; and thus are distorted.
For clearly figures could not be arbitrarily shifted and turned round in them if the curvature at each point were not the same in all directions.
Is the contrapositive argument. Inspired by the relationship between curvature and interpoint distances in the previous discussion, and through this contrapositive argument, Riemann seeks to strengthen the implication to P<=>Q, which says 'figures inscribed on the surface are undistorted' if and only if 'the curvature is constant'. The argument here is somewhat informal, as it is demonstrated by 'the measure relations on the manifoldness are entirely determined by the curvature', IE 'curvature behaviour' characterises 'interpoint distance behaviour'. Though this is of course supported by the prior derivations linking interpoint distances to curvatures.
On the other hand, however, the measure-relations of the manifoldness are entirely determined by the curvature; they are therefore exactly the same in all directions at one point as at another, and consequently the same constructions can be made from it: whence it follows that in aggregates with constant curvature figures may have any arbitrary position given them. The measure-relations of these manifoldnesses depend only on the value of the curvature, and in relation to the analytic expression it may be remarked that if this value is denoted by , the expression for the line-element may be written:
which is just the formula for the relationship between the metric and the curvature (don't know exactly how he gets to it). -
 fdrake
7.2kFor those of you wondering how all this math might apply in practice, I've got a worked example showing how the surface of a cylinder is actually flat.
fdrake
7.2kFor those of you wondering how all this math might apply in practice, I've got a worked example showing how the surface of a cylinder is actually flat.
The (curved) surface of a cylinder is just a circle boundary swept upwards. This means that any point on the surface of a cylinder can be given by an angle of rotation around its central axis , the distance from this central axis ; which is also the radius of its generating circle; and the distance travelled up from the circle's base .
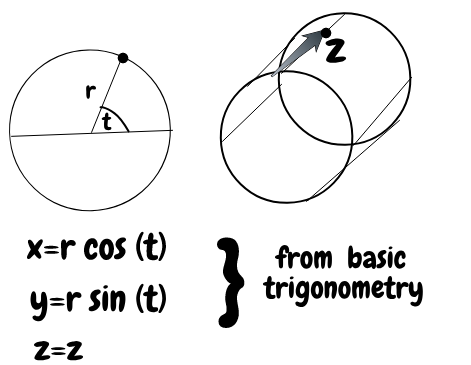
For ease, fix and let's make the circle centred at the origin of 3D space, the point (0,0). The typical point on the rolling surface of the cylinder (with radius 1) can then be expressed as:
The curvature of the cylinder is expressible by how the rates of change of tangent planes at each point interact, which means we need to differentiate with respect to each coordinate.
The angular changes which track the changes in the tangent plane with respect to variation in coordinates are tracked by the dot product between all pairs of rates of change. IE we have:
What each equation says is that (1) differential changes in angle as they contribute to the curvature are constant, , (2) differential changes in height as they contribute to the curvature are constant as well and that (3) moving a bit around the circle and moving a bit up the circle at the same time doesn't change the curvature.
The first (1) is associated with the infinitesimal length change along alone, . The second is associated with infinitesimal length change along alone, , and the final tells you how moving around and up at the same time changes the interpoint distance - not at all.
This means that the arc-length between two points on the surface can be measured just by how much one is rotated with respect to each other and how much one is above or below the other , the sum of the rotational amount and the distance up gives the infinitesimal change from one point to another. IE:
which is actually a flat metric. Thus, since a coordinate system exists which renders the arc-length between nearby points an independent function of each position, the surface of a cylinder is actually flat in the intrinsic sense. -
 fdrake
7.2kIII. Application to Space.
fdrake
7.2kIII. Application to Space.
Riemann takes his previous discussion and tries to relate it to physical space. Specifically, how does being able to see shapes/manifolds as 'spaces unto themselves' change what conceptions of space are possible? And how does this plurality of space concepts relate to empirical science?
He begins in §1 with a recap of the properties which characterise the geometry of an object.
§ 1. By means of these inquiries into the determination of the measure-relations of an n-fold extent the conditions may be declared which are necessary and sufficient to determine the metric properties of space, if we assume the independence of line-length from position and expressibility of the line-element as the square root of a quadric differential, that is to say, flatness in the smallest parts.
First, they may be expressed thus: that the curvature at each point is zero in three surface-directions; and thence the metric properties of space are determined if the sum of the angles of a triangle is always equal to two right angles.
Secondly, if we assume with Euclid not merely an existence of lines independent of position, but of bodies also, it follows that the curvature is everywhere constant; and then the sum of the angles is determined in all triangles when it is known in one.
Thirdly, one might, instead of taking the length of lines to be independent of position and direction, assume also an independence of their length and direction from position. According to this conception changes or differences of position are complex magnitudes expressible in three independent units.
(1) (Space is flat) if and only if (triangle angles sum together to 180 degrees). This is one way for curvature to be constant - everywhere 0.
(2) (Space has constant curvature, like a sphere surface) if and only if (the sum of angles in one triangle is the sum in all others). Note that the equivalence in (1) is also a case of this equivalence.
(3) Even weaker, if line lengths do not vary with origin point or orientation, how inter-point distances constrained to a manifold vary is always expressible as a function of the variables used in defining the manifold. (1) is a special case here since the 0 function is such a function, so is (2) since the constant function is such a function. (3) expresses the dependence of interpoint distances on the variables tracking the point on the manifold.
§ 2. In the course of our previous inquiries, we first distinguished between the relations of extension or partition and the relations of measure, and found that with the same extensive properties, different measure-relations were conceivable; we then investigated the system of simple size-fixings by which the measure-relations of space are completely determined, and of which all propositions about them are a necessary consequence; it remains to discuss the question how, in what degree, and to what extent these assumptions are borne out by experience. In this respect there is a real distinction between mere extensive relations, and measure-relations; in so far as in the former, where the possible cases form a discrete manifoldness, the declarations of experience are indeed not quite certain, but still not inaccurate; while in the latter, where the possible cases form a continuous manifoldness, every determination from experience remains always inaccurate: be the probability ever so great that it is nearly exact. This consideration becomes important in the extensions of these empirical determinations beyond the limits of observation to the infinitely great and infinitely small; since the latter may clearly become more inaccurate beyond the limits of observation, but not the former.
A discrete manifoldness is a purely categorical structure - it consists of distinct elements like A,B,C, rather than a continuum of points constrained by a function of position. I think all this is saying is that ways of counting discrete objects can error, but conceptually the procedure is quite simple - irrelevant of what the categorical structure is, counting's the same and 'to count' doesn't change meaning with respect to changes in counted elements. Measure relations of continuous manifoldness do, however, since curvature may change and thus change how measuring tapes glued to the manifold work.
In the extension of space-construction to the infinitely great, we must distinguish between unboundedness and infinite extent, the former belongs to the extent relations, the latter to the measure-relations. That space is an unbounded three-fold manifoldness, is an assumption which is developed by every conception of the outer world; according to which every instant the region of real perception is completed and the possible positions of a sought object are constructed, and which by these applications is for ever confirming itself. The unboundedness of space possesses in this way a greater empirical certainty than any external experience.
Extent probably means something similar to cardinality, or maybe a 'larger' concept. A continuum of points will have an infinite extent of points in it, since there are infinitely many, but nevertheless it may be bounded. Like the line between 0 and 1 on the number line.
Space is three dimensional, this is confirmed in every experience of it. Moreover, it doesn't 'just stop' at any point, making it unbounded (Riemann does not however seem to say why). However, Riemann portrays the unboundedness of space as 'possessing a greater empirical certainty than any external experience'. This is puzzling, on the one hand we have the unboundedness of space being supported by every experience, on the other we have that because or leading on from this unboundedness in situations of perception we can be more 'empirically certain' of this unboundedness than any mere synthesis of experiences allows.
I suspect I am misinterpreting the distinction between unboundedness and infinite extent, and both terms.
Welcome to The Philosophy Forum!
Get involved in philosophical discussions about knowledge, truth, language, consciousness, science, politics, religion, logic and mathematics, art, history, and lots more. No ads, no clutter, and very little agreement — just fascinating conversations.
Categories
- Guest category
- Phil. Writing Challenge - June 2025
- The Lounge
- General Philosophy
- Metaphysics & Epistemology
- Philosophy of Mind
- Ethics
- Political Philosophy
- Philosophy of Art
- Logic & Philosophy of Mathematics
- Philosophy of Religion
- Philosophy of Science
- Philosophy of Language
- Interesting Stuff
- Politics and Current Affairs
- Humanities and Social Sciences
- Science and Technology
- Non-English Discussion
- German Discussion
- Spanish Discussion
- Learning Centre
- Resources
- Books and Papers
- Reading groups
- Questions
- Guest Speakers
- David Pearce
- Massimo Pigliucci
- Debates
- Debate Proposals
- Debate Discussion
- Feedback
- Article submissions
- About TPF
- Help
More Discussions
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum








