-
 John Doe
200Sorry Wallows, I was waiting till we get a bit closer to the 13th just to tag everyone and remind them that this thread was kicking off.
John Doe
200Sorry Wallows, I was waiting till we get a bit closer to the 13th just to tag everyone and remind them that this thread was kicking off.
We're going to start with the Riemann paper on the 13th. I'm still open to what people want to do beyond that. It seems to me that we should probably just let that conversation go on as long as it goes. Meanwhile, people should feel free to nominate papers or books for discussion after that. -
 John Doe
200@Moliere @SapereAude@Terrapin Station @Wallows
John Doe
200@Moliere @SapereAude@Terrapin Station @Wallows
Hi all.
@fdrake has offered to lead a discussion of Bernhard Riemann's "On the Hypotheses which lie at the Bases of Geometry (1873)". Here is a link to the paper. If for some reason that link does not work for you, just google the paper - it seems to be pretty widely available. We will begin sometime around Sunday. It's a really cool paper so I definitely want to encourage people to read it - if you're not too busy it's sure to be worth the time you put into it. -
 DiegoT
318the movie was not too bad. I propose to follow the course on Magic, Religion and Science that UCLA uploaded to youtube some years ago. The lecturer is amazing; apparently she left teaching to do comedy; but she´s very intelligent and knowledgeable and explains the concepts very well. She wears different hats so that we can find the lessons more easily. There is a bibliography to follow the course more in depth. I propose to watch the episodes and comment on the selected texts she mentions in them. Really interesting!
DiegoT
318the movie was not too bad. I propose to follow the course on Magic, Religion and Science that UCLA uploaded to youtube some years ago. The lecturer is amazing; apparently she left teaching to do comedy; but she´s very intelligent and knowledgeable and explains the concepts very well. She wears different hats so that we can find the lessons more easily. There is a bibliography to follow the course more in depth. I propose to watch the episodes and comment on the selected texts she mentions in them. Really interesting!
https://www.youtube.com/watch?v=K3Zx-qcNZf4 -
 fdrake
7.2k
fdrake
7.2k
One of the reasons why it's so dense is because he's inventing lots of, what are now distinct, mathematical concepts at once. But he's not using the usual words for them (most of the time). EG, n-ply extended magnitudes seem to be n dimensional vector spaces, discrete manifoldness and its elements are like countable sets, continuous manifoldness and its elements are like the real numbers between [0,1], quanta are either elements of countable sets or bounded, connected regions of (possibly higher dimensional) space. Things like (paraphrasing) "mathematicians might unhesitatingly found the theory of discrete magnitudes upon the notion that certain things are to be found equivalent' seem to be ur forms of things like natural numbers being defined as bijection isomorphism classes of finite sets (eg, {a,b,c} and {d,e,f} are just relabelled forms of each other and both could represent the number 3). And this is all just stuff on the first page.
So yes, it's hard going, even for someone with lots of training in math. -
 Streetlight
9.1kI'm not sure when we're supposed to start, but I was reading the introduction to the Riemann paper and was making notes, so I figure I'll do a quick post on the 'Plan of the Investigation' section in case it helps people orient themselves.
Streetlight
9.1kI'm not sure when we're supposed to start, but I was reading the introduction to the Riemann paper and was making notes, so I figure I'll do a quick post on the 'Plan of the Investigation' section in case it helps people orient themselves.
The basic idea is this: Riemann is saying that space as we know it - the kind of space in which me move around and live - is but a particular case of a more general notion of space which can be constructed from 'general notions of magnitude'. Or, put the other way, one can construct more kinds of spaces out of 'general notions of magnitude' than only the kind of the space in which we live in.
To this degree, the 'general notions of magnitude' are too general to properly model (our) space: if you begin with such general notions and nothing else, you won't be able to properly model our space with enough specificity. So to such general notions, one needs to add another ingredient: 'experience'. Hence:
"The propositions of geometry cannot be derived from general notions of magnitude, but ... the properties which distinguish space from other conceivably triply extended magnitudes are only to be deduced from experience".
So Riemann here develops a tension between general notions on the one hand and experience on the other, the latter of which includes 'matters of fact' (a kind of rationalism vs. empiricism dichotomy). And each 'side' has its own issues when it comes to space. On the 'side' of the rational, general notions are 'too general' to get at the specificity of space, and on the side of the empirical, 'several systems of matters of fact' can be used to 'determine the measure-relations of space'.
Or to put it differently, if there is a one-to-many relation between general notions of magnitude and our space (the general notion can give rise to many notions of space, of which ours is only one), there is, on the other hand, a many-to-one relation between 'systems of matters of fact' and our space (several systems of matters of fact can give rise to our space). That all said, the main 'system of matters of fact' has so far been Euclidean geometry (there can be others).
So given that there is no one-to-one correspondence between 'matters of fact' and our space, Riemann wants to ask after the 'probability' of such matters of fact - which I understand to be something like 'how probable is it that these matters of fact obtain, and not others?'. And also, given that we can go 'beyond the limits of observation', both at the level of facts and at the level of notions, how 'justified' would we be in doing so? Which I read as something like: 'is there any good reason to 'go beyond the limits of observation' and indulge in what we 'can' do over what 'is'?
I'm a bit iffy on my reading of this last bit, and am keen to see what others make of it. This bit: ""we may therefore investigate their probability,which within the limits of observation is of course very great, and inquire about he justice of their extension beyond the limits of observation, on the side of both the infinitely great and of the infinitely small". -
 fdrake
7.2kGuess I'll start today rather than tomorrow since tomorrow is busy. Here is a copy of the paper that's in plain text (so it allows quotation through copy/paste).
fdrake
7.2kGuess I'll start today rather than tomorrow since tomorrow is busy. Here is a copy of the paper that's in plain text (so it allows quotation through copy/paste).
Section 1: Plan of the Investigation.
It is known that geometry assumes, as things given, both the notion of space and the first principles of constructions in space. She gives definitions of them which are merely nominal, while the true determinations appear in the form of axioms.
I think the first sentence is an attempt to characterise the study of geometry. In my mind here I'm imagining he's talking about Euclid's elements as an example. The logical structure Riemann seems to be given to geometry is as a composite of:
(1) intuitions about space "the notion of space"
(2) (mathematical) rules which characterise the intuitions.
and these things are treated as a unit; that we have characterised all our intuitions about space, the space construction/model within mathematics (Euclidean space), through a successful determination of mathematical rules which characterise them.
So when Riemann writes " She gives definitions of them which are merely nominal, while the true determinations appear in the form of axioms.", he's saying that the supposed unity between (1) and (2) is actually just a predisposition of interpretation, and we can do with (2) alone to characterise a notion of space. Thus the fact that:
The relation of these assumptions remains consequently in darkness; we neither perceive whether and how far their connection is necessary, nor a priori, whether it is possible.
is ensured by the duality of mathematical rules characterising the mathematical nature of space, but we suppose that these rules, the axioms, give a complete characterisation of the intuitions we may have, (1). What Riemann is doing here is driving a wedge between intuitions of space as studied in (Euclidean) geometry and the necessity of application of those intuitions to all possible mathematical space concepts.
I imagine anyone with a familiarity of the Transcendental Aesthetic in Kant will already find this argument extremely interesting. So I think Street is very right in their emphasis that:
The basic idea is this: Riemann is saying that space as we know it - the kind of space in which me move around and live - is but a particular case of a more general notion of space which can be constructed from 'general notions of magnitude'. Or, put the other way, one can construct more kinds of spaces out of 'general notions of magnitude' than only the kind of the space in which we live in. — StreetlightX
and I would add that this follows from our ability to play with axioms to posit new spaces to have intuitions about. Or inversely to refine and add specificity to our intuitions of (maybe Euclidean) space by codifying them in appropriate axioms. -
 fdrake
7.2kStill in "Plan of the Investigation", now the second paragraph.
fdrake
7.2kStill in "Plan of the Investigation", now the second paragraph.
From Euclid to Legendre (to name the most famous of modern reforming geometers) this darkness was cleared up neither by mathematicians nor by such philosophers as concerned themselves with it. The reason of this is doubtless that the general notion of multiply extended magnitudes (in which space-magnitudes are included) remained entirely unworked. I have in the first place, therefore, set myself the task of constructing the notion of a multiply extended magnitude out of general notions of magnitude. It will follow from this that a multiply extended magnitude is capable of different measure-relations, and consequently that space is only a particular case of a triply extended magnitude. But hence flows as a necessary consequence that the propositions of geometry cannot be derived from general notions of magnitude, but that the properties which distinguish space from other conceivable triply extended magnitudes are only to be deduced from experience. Thus arises the problem, to discover the simplest matters of fact from which the measure-relations of space may be determined; a problem which from the nature of the case is not completely determinate, since there may be several systems of matters of fact which suffice to determine the measure-relations of space - the most important system for our present purpose being that which Euclid has laid down as a foundation. These matters of fact are - like all matters of fact - not necessary, but only of empirical certainty; they are hypotheses. We may therefore investigate their probability, which within the limits of observation is of course very great, and inquire about the justice of their extension beyond the limits of observation, on the side both of the infinitely great and of the infinitely small.
Hoo boy.
From Euclid to Legendre (to name the most famous of modern reforming geometers) this darkness was cleared up neither by mathematicians nor by such philosophers as concerned themselves with it.
So Riemann's saying that the mathematical accounts in history, while possibly providing different conceptions of space (as comparing Euclid to Legendre and later Gauss), did little to remove the void of darkness between mathematical intuitions of space and their axiomatisations; to name the darkness, I think it is characterised by the questions: "What do our intuitions (1) say about the axioms (2)? And what do the (2) axioms say about our intuitions (1)?", characterising the relationship between (1) and (2) from both sides as it were.
The reason of this is doubtless that the general notion of multiply extended magnitudes (in which space-magnitudes are included) remained entirely unworked.
Space magnitudes seem to be treated as 0 dimensional points, 1 dimensional lines, 2 dimensional areas and 3 dimensional volumes. Space-time in the Einsteinian sense would also be a 'multiply expanded magnitude' and space concept.
So what's the commonality here? I believe when Riemann is considering a 'multiply extended magnitude', he's thinking of a vector of the appropriate dimension, a 'position' in a space. So a 1 dimensional line becomes <x>, ranging from -1 to 1 draws the usual section of the number line between [-1,1], a 2 dimensional area becomes characterised in the form <x,y>, with constraints on <x,y> to specify the area (eg x^2+y^2<=1 for a circle centred at the origin with radius 1) or <x,y,z> to specify a volume (with x^2+y^2+z^2<=1 for a sphere centred at the origin with radius 1). (Edit: though it's worthwhile noting here that 'coordinate system' is maybe a better representation of the concept, but the distinction between vector space and coordinate system probably doesn't matter at this point in the exegesis, in which the concepts are fuzzy) The idea of a 'multiply extended' magnitude is just that of a collection of 1 dimensional magnitudes.
Note at this point we have a sense for the 'size' of 1 dimensional, 2 dimensional and 3 dimensional magnitudes - length, area, volume-, and we also have multiply extended magnitudes being a collection of independently varying 1 dimensional magnitudes (the x and y directions in the plane, say, are both 1 dimensional magnitudes which together form a 2 dimensional magnitude). So Riemann sets himself the task of:
I have in the first place, therefore, set myself the task of constructing the notion of a multiply extended magnitude out of general notions of magnitude.
defining/mathematically characterising/axiomatising notions of size (like length, area, volume) for multiply extended magnitudes (like lines, circles, spheres). But it is worthwhile to note that Riemann is explicitly considering notions of space, so we're considering things 'one layer back' from lines, circles, spheres - we're considering ways of linking geometries to sizes. The first example of which in the paper is trying to construct/axiomatise the usual notion of length/area/volume in Euclidean space. So when Riemann says:
It will follow from this that a multiply extended magnitude is capable of different measure-relations, and consequently that space is only a particular case of a triply extended magnitude.
he's talking about the fact that completely characterising, say, the relationship between space and volumes mathematically - you can change this relationship in accord with some notion end up with an inequivalent notion of space. This drives a 'hard wedge' as it were between the necessity of the relationship between (1) the space intuition and (2) its complete axiomatisation; there is now more than one space intuition/notion, revealed by the ability to modify axioms/characterisations of space. Shifting vocabularies, there's no unique mathematical 'space intuition' a priori, since we can characterise others - and perhaps, tentatively, this means the reason for the darkness between (1) and (2) is an elision inherent in previous geometric thought generated by the belief that studying space intuitions always meant articulating a single a priori notion of space (eg Euclidean space, that which is described by Euclid in his Elements). Because of this
hence as a necessary consequence that the propositions of geometry cannot be derived from general notions of magnitude
(because of the plurality of magnitude notions revealed by Riemann's approach) and thus:
the properties which distinguish space from other conceivable triply extended magnitudes are only to be deduced from experience.
we must recognise what space-like notion is appropriate for whatever purposes we may have. Riemann then seeks to find indicators - necessary and sufficient conditions / characterisations - of notions of space (and multiply extended magnitudes more generally) - of which space concept is appropriate for which purpose.
Thus arises the problem, to discover the simplest matters of fact from which the measure-relations of space may be determined; a problem which from the nature of the case is not completely determinate, since there may be several systems of matters of fact which suffice to determine the measure-relations of space - the most important system for our present purpose being that which Euclid has laid down as a foundation.
and moreover the existence of multiple n-dimensional magnitude concepts (like the link between 2 dimensional spaces and areas) severs the a priori connection between Euclidean space(s) and space, as n dimensional magnitude, simpliciter.
One illustrative example here is that for distances on the surface of the Earth, if they're short we can use Euclidean geometry to calculate them, but if they're long we can't - the surface of a sphere is not Euclidean, it wraps around itself, it has curvature and so on.
Thus, the a priori necessity of space being Euclidean space, or more generally of space being uniquely characterised, is broken by the plurality of n dimensional magnitudes and measures of their length/area/volume. In essence, Riemann is playing a game of constructing counterexamples to Euclidean space after characterising precisely what it is! Find the boundaries of the concept, find the exceptions, and vice versa.
Because we no longer have the a priori necessity of our calculations about space, destroyed by the non-uniqueness of space concepts, this renders which space concepts nature can be modelled by as a matter of investigation:
These matters of fact are - like all matters of fact - not necessary, but only of empirical certainty; they are hypotheses. We may therefore investigate their probability, which within the limits of observation is of course very great, and inquire about the justice of their extension beyond the limits of observation, on the side both of the infinitely great and of the infinitely small.
and of purely mathematical consequences/assumptions of them ('beyond the limits of observation').
The relationship to infinitely great and infinitely small probably connotes the fact that Riemann will be studying space at multiple scales; the geometry relationship between 2 dimensions and volumes, say, becomes defined with respect to infinitely small variations (like dx and dy in calculus), and it may be that on larger scales different mathematical patterns can hold even within the same notion of space (like my sphere example above).
Edit: note that when I'm using <> to surround something, that's notation that refers to a coordinate system being in play. So EG <x> denotes a position on (something like/for example) the real line, <x,y> denotes a position in in the plane (or something like it/for example) and so on. -
 Moliere
6.5k@StreetlightX @fdrake
Moliere
6.5k@StreetlightX @fdrake
That contrast between space-as-concept and space-as-experienced helped me parse out the last paragraph a lot, so thanks for that. There is something I think I'd highlight in the intro, though, from the beginning:
It is known that geometry assumes, as things given, both the notion of space and the first principles of constructions in space. She gives definitions of them which are merely nominal, while the true determinations appear in the form of axioms. The relation of these assumptions remains consequently in darkness; we neither perceive whether and how far their connection is necessary, nor a priori, whether it is possible.
From Euclid to Legendre (to name the most famous of modern reforming geometers) this darkness was cleared up neither by mathematicians nor by such philosophers as concerned themselves with it.
I think that the "darkness" referred to above is the relations between the assumptions geometry has -- I take it he means the 5 postulates of Euclids system as the primary example, though he does allude to the thought that there can be other axioms. As I read him here it seems that Reimann is motivated to understand the possible justification for just these axioms, and wants to understand the relationship they have to one another -- whether they are necessary, whether they are universal, and whether they are even possible.
Nothing to disagree with here, just highlighting something that leapt out. It does seem, as we go on, that he believes that these axioms are not necessary a priori, but have to be justified by reference to experience -- and so the project changes to ask just how far we are justified in trusting just these axioms.
In particular why this leapt out for me was because of the next sentence I sat puzzling over for awhile:
it. The reason of this is doubtless that the general notion of multiply extended magnitudes (in which space-magnitudes are included) remained entirely unworked
I pretty much just had to take this on faith to keep on going, but I didn't understand why this was even the next step in the line of reasoning - much less why it was doubtless. -
 fdrake
7.2kAnother note I have is that notions like coordinate system, manifold, set and so on are not precisely established in mathematical discourse at the minute. The paper is 'conceptually positioned', so to speak, in wrestling with appropriate definitions of the mathematical concepts it treats. In a certain sense, looking at the history of mathematics as a field of study lets us peer under the bonnet of mathematical formulae and theorems to the imaginative background they fall out of.
fdrake
7.2kAnother note I have is that notions like coordinate system, manifold, set and so on are not precisely established in mathematical discourse at the minute. The paper is 'conceptually positioned', so to speak, in wrestling with appropriate definitions of the mathematical concepts it treats. In a certain sense, looking at the history of mathematics as a field of study lets us peer under the bonnet of mathematical formulae and theorems to the imaginative background they fall out of.
This also means, then, that whenever I'll use a more contemporary mathematical example or analogy, it will make an omission through excessive clarity - like reading the idea of a vacuum back into the aether, or treating phlogiston as a rung on the scientific ladder used to climb toward energy. -
 fdrake
7.2kit. The reason of this is doubtless that the general notion of multiply extended magnitudes (in which space-magnitudes are included) remained entirely unworked — Moliere
fdrake
7.2kit. The reason of this is doubtless that the general notion of multiply extended magnitudes (in which space-magnitudes are included) remained entirely unworked — Moliere
The modern notions of coordinate systems and vectors weren't well established at the time of Riemann's writing. Moreover, as will become more clear (I think) in the first section, he sees these 'coordinate system' like concepts as just an expression of something more basic about the objects considered. This desire to treat objects, surfaces and so on 'intrinsically', rather than through the 'extrinsic' ideas/representational powers of coordinate geometry is a style of thinking Riemann helped found in this paper - where we can see many germinal forms of now precisely articulated mathematical concepts. -
 fdrake
7.2kI think that the "darkness" referred to above is the relations between the assumptions geometry has -- I take it he means the 5 postulates of Euclids system as the primary example, though he does allude to the thought that there can be other axioms. As I read him here it seems that Reimann is motivated to understand the possible justification for just these axioms, and wants to understand the relationship they have to one another -- whether they are necessary, whether they are universal, and whether they are even possible. — Moliere
fdrake
7.2kI think that the "darkness" referred to above is the relations between the assumptions geometry has -- I take it he means the 5 postulates of Euclids system as the primary example, though he does allude to the thought that there can be other axioms. As I read him here it seems that Reimann is motivated to understand the possible justification for just these axioms, and wants to understand the relationship they have to one another -- whether they are necessary, whether they are universal, and whether they are even possible. — Moliere
Third post in a row, sorry fellow mods, I got too excited and hit the 'Post Comment' button too quickly.
I think this is about right, wondering how Euclid's system 'fell out of' our experiences and intuitions is probably something driving Riemann's engagement here; and the ability to define what makes a concept of space like the one dealt with in Euclid invites/renders possible mathematical suppositions contrary to it.
I suppose this relates to broader themes in philosophy. Mathematics is usually considered a largely a priori exercise - yet here we are with a certain plurality and non-determination within it, as if there are competing images/accounts to be had. All of which equally good and true in supposition - treating them purely mathematically -, but now the plurality invites questions of which suppositions are right. To borrow Kantian vocabulary, we either sever the pure intuition of space from the objects it phenomenally conditions or admit a multiplicity of pure intuitions of space which may apply in different mathematical or experiential contexts.
Edit: another possibility is that, say, 'the' pure intuition of space isn't necessarily captured by Euclid's work and presuppositions, driving a wedge between the intuitions embodied in Euclid's assumptions and the necessity of their connection with objects. 'The' pure intuition may admit of multiple space concepts consistent with it. -
 fdrake
7.2k
fdrake
7.2k
I imagine that even without understanding the math, as I won't at points without lots of work (I have a first principles/pedagogical differential geometry textbook I'm referring to to orient myself, I can definitely not send it to people if they want it), I still think it's possible to get something out of the flow of the argument. Bracketing the specifics of the mathematical reasoning and treating it like a phenomenology of space; or a highlighter of differences and commonalities between the phenomenology of space and possible ways of conceiving it mathematically. -
 John Doe
200Hi all, really sorry I missed out on the first day - something serious has come up all of a sudden so unfortunately I may be posting a little sporadically over the next several days. @fdrake's posts are utterly fantastic so I'm going to try my best to address them today. I think following what just said, maybe the best way to do this paper is if I act as a foil to @fdrake, trying to respond to your posts from the perspective of having no mathematical knowledge. (It won't be that hard to pretend. :wink:) @Wallows -- I get the impression you know a lot more math than I do! What do you say to sticking together here and seeing how the paper comes out if we try to work through the math from a place of total ignorance?
John Doe
200Hi all, really sorry I missed out on the first day - something serious has come up all of a sudden so unfortunately I may be posting a little sporadically over the next several days. @fdrake's posts are utterly fantastic so I'm going to try my best to address them today. I think following what just said, maybe the best way to do this paper is if I act as a foil to @fdrake, trying to respond to your posts from the perspective of having no mathematical knowledge. (It won't be that hard to pretend. :wink:) @Wallows -- I get the impression you know a lot more math than I do! What do you say to sticking together here and seeing how the paper comes out if we try to work through the math from a place of total ignorance? -
 Shawn
13.5k
Shawn
13.5k
Sounds good to me. I won't comment much henceforth and there really isn't much to comment on either way for the better. I wish we could group work on a PDF with comments on the side of highlighted text to be more precise as this text contains a lot of content despite its brevity. -
 Moliere
6.5kI was reading another paper about Reimann online, and from it I gleaned that I was sort of misreading "manifoldness" -- whereas I was sort of analogizing it with a vector before -- which I really only understand to be a magnitude with a direction -- it seemed to make more sense that Reimann is actually talking about the coordinate system itself. So Euclid or Cartesian coordinates are one example of a manifold, but the manifold could differ from these.
Moliere
6.5kI was reading another paper about Reimann online, and from it I gleaned that I was sort of misreading "manifoldness" -- whereas I was sort of analogizing it with a vector before -- which I really only understand to be a magnitude with a direction -- it seemed to make more sense that Reimann is actually talking about the coordinate system itself. So Euclid or Cartesian coordinates are one example of a manifold, but the manifold could differ from these.
That probably should have leapt out as obvious from the beginning, since I know Reimann is associated with notions of space itself bending, but I thought I'd put that out there to see if others agree. -
 fdrake
7.2kI was reading another paper about Reimann online, and from it I gleaned that I was sort of misreading "manifoldness" -- whereas I was sort of analogizing it with a vector before -- which I really only understand to be a magnitude with a direction -- it seemed to make more sense that Reimann is actually talking about the coordinate system itself. So Euclid or Cartesian coordinates are one example of a manifold, but the manifold could differ from these. — Moliere
fdrake
7.2kI was reading another paper about Reimann online, and from it I gleaned that I was sort of misreading "manifoldness" -- whereas I was sort of analogizing it with a vector before -- which I really only understand to be a magnitude with a direction -- it seemed to make more sense that Reimann is actually talking about the coordinate system itself. So Euclid or Cartesian coordinates are one example of a manifold, but the manifold could differ from these. — Moliere
I think this is right. A manifold is essentially an object with a coordinate system associated with it. So like a sphere, or the boundary of a circle, or even the entirety of our infinite space in any number of dimensions.
A key insight in the mathematics of manifolds is that 'the' coordinate systems is kind of extraneous to it, in the same sense that a circle is still the same circle no matter whether you express all its points through the usual (x,y) coordinates, or in terms of a distance from its centre r and an angle of rotation t - the shape doesn't change, the circle is the circle, we've just altered its manner of representation.
This provokes defining manifolds with respect to all the coordinate systems they are compatible with, so definitions of manifolds quantify over coordinate systems and ensure that these coordinate systems 'chart' neighbourhoods around every point on the manifold, and moreover the coordinate systems associated with a manifold have to be able to be transformed seamlessly into each other. If this seems abstract, imagine that we rotate the y axis in the x-y plane 45 degrees to the right, the underlying space is the same, and we have a formula to translate positions assigned in the original x-y plane coordinates to the rotated version (a similar construction exists for the circle example, r^2 = x^2 + y^2, the angle t being measured from the right part of the x-axis through trigonometry, tan(t)=y/x).
The highlights in the modern definitions are:
A (smooth) manifold is a set of points considered together with a set of coordinate systems. These points and the coordinate systems must behave in the following way:
(1) that every neighbourhood of a point in a manifold (think of a closed loop drawn around the point = neighbourhood) has to be able to be expressed in some coordinate system associated with it.
(2) that every coordinate system associates neighbourhoods of points to the usual mathematical Euclidean space in a one-to-one fashion.
(3) The coordinate systems associated with a manifold must be able to be smoothy transformed into each other (like a coffee cup into a donut in the usual example).
(1) mirrors the idea of 'localised geometry' or relating to the focus Riemann has on infinitesimal calculations in the paper; the infinitesimal parts might be Euclidean or not, the space might be locally Euclidean but over large (or infinite) regions of space not; hence concerns of 'going beyond the limits of observation' - manifolds both have an infinitesimal aspect (localised geometries) and an infinite one ('really big' regions might not respect the infinitesimal relationships/local geometries derived or ascribed). [Condition (2) ensures, however, that we have an object which is locally Euclidean, but Riemann introduces this conception later.]
(2) mirrors the concerns Riemann has about quartics and quadratics in the distance notions ('square root of a quadric (quadratic, x^2 terms)' vs 'fourth root of a quartic (x^4 terms)', the notions that have 'square root of a quadric' are locally Euclidean in the way our universe and perceptions (allegedly) are.
(3) mirrors the concerns of intrinsic vs extrinsic thinking, nothing about a shape should depend on how we describe the positions of points on it, this would be like saying the map manipulates the territory, or the surface of the Earth is given its shaped by our lines of longitude and latitude. -
 fdrake
7.2k
fdrake
7.2k
So the specialisations bit, this is now discussing §1 in the paper:
Magnitude-notions are only possible where there is an antecedent general notion which admits of different specialisations. According as there exists among these specialisations a continuous path from one to another or not, they form a continuous or discrete manifoldness; the individual specialisations are called in the first case points, in the second case elements, of the manifoldness.
We can only have magnitudes expressed mathematically if there exists a general concept of size (relating to previous philosophical concerns) which we can tailor to specific contexts. Like we can imagine lengths as represented by numbers with a length dimension, times as numbers with a time dimension, collections of distinct objects with numbers (cardinalities) that give how many distinct objects there are.
The distinction between continuous and discrete manifoldnesses seems to depend on whether we can 'travel' from one element of the manifold to another 'through other elements laying within the manifoldness' - so we can link two points on a bit of paper with a line, making the sheet of paper continuous manifoldness, but we couldn't link the letters A and B with a letter 'between' them, or the numbers 1 and 2 with a natural number 'between' them.
Another way of constructing a discrete manifoldness, say, would be to imagine two non-overlapping spheres in space. There are points between them, but no points between them which are also points on the sphere - and thus no points between them which are part of the coordinate systems giving the points on either sphere, so paths between them are blocked, making a discrete manifoldness.
The 'ability to travel through/on the manifold from one point to another' is related to points (1) and (2) in my previous post discussing the modern notions of manifold ('manifoldness') that developed after Riemann. It is related to point (1), because this allows us to express 'local changes of position' using the coordinate system. This equates to the condition of being locally connected. But the notion Riemann discusses is more broad, I think, because guaranteeing that all the 'specialisations' (points in the continuous case) have a continuous path from one to the other on/through the manifold would make it a connected space. Though I think that the usual Riemannian manifolds - the one the paper inspires - are indeed fully connected in the 'continuous path from every point to every other' sense. Note that coordinate systems are used to express these paths, but the paths themselves are part of the manifold and not tied to the specific coordinate system used to express the path.
(Edit: as an aside, look at this pathological motherfucker, connected but not path connected or locally connected!)
Riemann goes on to say that:
Notions whose specialisations form a discrete manifoldness are so common that at least in the cultivated languages any things being given it is always possible to find a notion in which they are included.
I imagine this commonality as coming from him having countable or finite collections of object in mind. So we can count chairs or coffee cups or insects or items of food. So the aside he makes:
(Hence mathematicians might unhesitatingly found the theory of discrete magnitudes upon the postulate that certain given things are to be regarded as equivalent.)
suggests something like the following procedure. We might define the number, 2, say as the equivalence class of sets with 2 elements, so {A,B} and {C,D} could both be regarded as exemplars of the number 2, since both have 2 elements. They're equivalent because we require the same number of discrete labels (A,B for the first, C,D for the second) to attach to all the elements. This line of thought was actually developed, and numbers can be characterised as collections of sets with their elements relabelled (IE that one-to-one correspondence holds between the two, and all other sets with 2 objects in 'em). I also think he has distinct objects in mind that we usually encounter because he contrasts the massive number of cases where we can count stuff or label stuff exhaustively vs cases where we cannot; examples of continuous manifoldness.
On the other hand, so few and far between are the occasions for forming notions whose specialisations make up a continuous manifoldness, that the only simple notions whose specialisations form a multiply extended manifoldness are the positions of perceived objects and colours. More frequent occasions for the creation and development of these notions occur first in the higher mathematic.
IE, the canonical examples of continuous manifoldness being colour spectra and position in space. But the expressive power of math is much greater than this; suppose there is a continuous path between every pair of elements, then we have a continuous manifoldness by definition. We could do this with space-time, we could express the motion of a car with respect to the driver's wheel turning angles and its forward motion, we could aggregate colours together with sound frequencies or perceived colours together with frequency measurements, and these things would be examples of continuous manifoldness (since they strongly resemble 2-D Euclidean space) since mathematics allows us the freedom to consider both together, at once, as a unitary abstraction and study/ascribe relationships to the components. Note that these space-like concepts do not correspond to our usual phenomenological spatial directions, so the notion of 'multiply extended magnitude' is broader. We could even consider, say, mass as a continuous manifoldness (since it's a real number greater than or equal to 0!), and give it a local geometry (flat in this case).
The notion of splitting manifolds up into components, informally independent directions of variation, is the subject of §2, the next paragraph (but I haven't finished writing about §1 yet). -
 Streetlight
9.1kTabled summary of §1:
Streetlight
9.1kTabled summary of §1:

(Ahh, I messed up the last bit of this table: the type of measure for discrete manifolds should be one magnitude as a measure of another, not as part of another. I copy-pasted the wrong text!).
Now, the tricky thing is to understand the two types of measurement for manifolds. I think a visual representation will be helpful:
(1) Superposition of magnitudes:

(2) One magnitude as part of another:
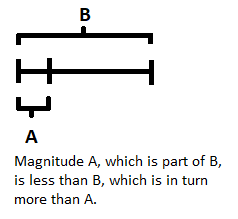
It is this second form of measurement, conducted on continuous manifolds which cannot be superposed, which "forms a general division of the science of magnitude in which magnitudes are regarded not as existing independently of position and not as expressible in terms of a unit, but as regions in a manifoldness." The language in this is a bit archaic, but a 'general division of the science of magnitude' can be translated into something like "this kind of measurement is one kind of measurement in a larger 'science of measurement' which also includes other kinds of measurement".
Note the two conditions of this kind of measurement:
(A) The magnitude cannot be regarded as independent of position (within the manifold).
(B) The magnitude is not expressible in terms of a unit.
Which one can summarise as: the measure of a magnitude of this kind is immanent to the manifold itself, and not extrinsic to it. Gonna include a quote from Manuel DeLanda which I find very helpful in explaining in why this kind of thing is novel in math:
"In the early nineteenth century, when Gauss began to tap into differential [mathematics], a curved two-dimensional surface was studied using the old Cartesian method: the surface was embedded in a three-dimensional space complete with its own fixed set of axes; then, using those axes, coordinates would be assigned to every point of the surface; finally, the geometric links between points determining the form of the surface would be expressed as algebraic relations between the numbers. But Gauss realized that the calculus, focusing as it does on infinitesimal points on the surface itself (that is, operating entirely with local information), allowed the study of the surface without any reference to a global embedding space. Basically, Gauss developed a method to implant the coordinate axes on the surface itself (that is, a method of “coordinatizing” the surface) and, once points had been so translated into numbers, to use differential (not algebraic) equations to characterize their relations. As the mathematician and historian Morris Kline observes, by getting rid of the global embedding space and dealing with the surface through its own local properties 'Gauss advanced the totally new concept that a surface is a space in itself'.
The idea of studying a surface as a space in itself was further developed by Riemann. Gauss had tackled the two-dimensional case, so one would have expected his disciple to treat the next case, three-dimensional curved surfaces. Instead, Riemann went on to successfully attack a much more general problem: that of N-dimensional surfaces or spaces. It is these N-dimensional curved structures, defined exclusively through their intrinsic features, that were originally referred to by the term “manifold”. Riemann’s was a very bold move, one that took him into a realm of abstract spaces with a variable number of dimensions, spaces which could be studied without the need to embed them into a higher-dimensional (N+1) space" (Delanda, Intensive Science and Virtual Philosophy).
--
The end of §1 basically tries to say why this kind of measurement is so important: it allows one to make good on certain mathematical advances by Abel, Lagrage, etc, and it allows for a fuller investigation of multiply extended manifolds. -
 John Doe
200Okay, so as I promised yesterday, I want to try to analyze, or at least summarize, each section of this paper in mostly non-mathematical terms. This may turn out to be a really dumb idea that contributes nothing. But I think that the paper is so dense and mathematically sophisticated that it can obscure the more straightforward aspects of the argument. I’m therefore at least going to try and see where I can get by treating each section as providing an argument-structure typical of a basic Philosophy 101 paper, an argument which then gets fleshed out through the introduction of mathematical concepts and arguments.
John Doe
200Okay, so as I promised yesterday, I want to try to analyze, or at least summarize, each section of this paper in mostly non-mathematical terms. This may turn out to be a really dumb idea that contributes nothing. But I think that the paper is so dense and mathematically sophisticated that it can obscure the more straightforward aspects of the argument. I’m therefore at least going to try and see where I can get by treating each section as providing an argument-structure typical of a basic Philosophy 101 paper, an argument which then gets fleshed out through the introduction of mathematical concepts and arguments.
Plan of the Investigation - Okay, the organization of this section is straightforward (though where he lands on certain philosophical questions certainly is not). He’s introducing the topic; orienting the conversation; telling us what he thinks is wrong with previous approaches; how he’s going to fill in this gap; what his argument will be. Again, like basically any philosophy paper.
These are the basic questions I think we should be asking ourselves in this section:
(1) What is the meaning of the title - i.e. the scope of the work?
(2) What is the problem the author is addressing?
(3) Which previous solutions or ways of thinking about this problem is he attacking? In what way are they wrong or misguided?
(4) What sort of solution is he going to offer us instead? How is he going to go about doing that?
Paragraph 1:
Literature Review: Geometry assumes as given — let’s call this ‘the Given’ of geometry — (a) the notion of space; (b) first principles of constructions in space.
But geometry gives definitions of this ‘Given’ in name only; the actual work of the sort that interests us philosophically (determinate truth) appears in the form of axioms.
Oversight in the Literature: This leads Riemann to a question which will guide the paper: What is the relationship between this taken-for-granted notion of space and constructions in space (the ‘Given’ of geometers) and the type of determinate truth which geometers arrive at via axiomatization?
Problem: I take it that this is a straightforward philosophical puzzle that actually interests most members of this forum: What does mathematics reveal about the nature of space? How does our intuitive understanding of space (derived from us being a particular sort of creature with a special type of bodily experience of space) affect our mathematics? Is it possible to achieve a more disinterested and perfect mathematical understanding of space if we remain steadfastly committed to untangling the role that anthropocentrism has played in various approaches to geometry? Is a wholly disinterested mathematical notion of space ‘more true’ than the sort of space in which we live and move and have our being? (These are all still very contemporary debates.)
Paragraph 2:
Literature Review: Philosophers and Mathematicians (including the most renowned) have failed to address adequately the concerns raised in Para 1. — Why? — Because of a conceptual failure to understand a new concept that I shall be introducing: Multiply Extended Magnitudes. (MEM)
Problem How should we understand a Multiply Extended Magnitude — and consequently answer the problem set out in this paper (see para 1)? Well, we will have to show how:
General Notions of Magnitude —> Multiply Extended Magnitude.
(So if you're having trouble with the math just remember to contextualize it in this way: We have a mathematical problem, GNM --> MEM, and we're going to see how answering this will be of basic interest to the philosophical problem which likely interests all of us.)
Consequences: (a) Triply Extended Magnitude is more general than Space (i.e. ‘the Given’ of previous geometry; i.e. intuitive space). (b) Experience alone distinguishes intuitive space from other conceivable triply extended magnitudes. (TEM)
Problem: If “experience” is the sole means by which we can understand intuitive space — how do we understand what “experience” is with respect to the role that it’s playing in our ability to understand space mathematically (viz. as one among many conceivable TEM)? How does the determination of ‘intuitive’ space work?
To answer the question of previous posters about “simplest matters of fact” I read this — perhaps stupidly — as a matter of the straightforward “relation” problem being dealt with in para. 1; do we get from mathematics to intuition via facts/theory/axioms/deduction, etc.? Or is there a different sort of intelligibility at work? If the latter then we arrive at the “several systems of matters of fact” — namely, that different creatures will so-to-speak “interpret" space differently in their lived experience, but there may be an insoluble gap between how we can understand these different systems mathematically versus in lived experience.
If I may put this in Heidegger terms. If the intelligibility of the ready-to-hand understanding of space is necessary to arrive at the present-at-hand understanding of space then we may not be able to get at the variety of ready-to-hand understandings which the mathematics suggests would be available to different types of embodied creatures.
To put this in terms of the “transcendental aesthetic”: Aliens may very well experience a different sort of ‘intuitive space’, but they would need this experience in order to understand how the TEM describes this space. Just as we need our intuitions in order to get from the TEM to our intuitive space.
To put the same point in yet another way: Euclidean geometry is possible only because we have lived in human space. An alien could not get to Euclidean geometry from within a different lived intuitive-space.
The Title: I’ll quote in full: “These matters of fact [viz. euclidean geometry] are - like all matters of fact - not necessary, but only of empirical certainty; they are hypotheses.”
Sorry this write-up was a little lame; hopefully in a couple days I will be less distracted and promise to do a better job of it. Really love everything I'm reading from you guys! -
 fdrake
7.2kFinishing my exegesis of §1
fdrake
7.2kFinishing my exegesis of §1
Definite portions of a manifoldness, distinguished by a mark or by a boundary, are called Quanta.
definite portions could be elements, like A in {A,B} portions of discrete manifoldness, distinguished by a mark (A). Or they could be points, like the circle with radius 1 centred at 0 in the plain. I want to emphasise along with Street (and highlight since it's super important), that treating the circle as a space unto itself, as a thing with its own properties independent of the coordinate system used to describe it, is a really novel way of thinking that Riemann helped create.
Their comparison with regard to quantity is accomplished in the case of discrete magnitudes by counting, in the case of continuous magnitudes by measuring.
I'll take it that counting is straightforward. But note here that Riemann is operationalising the concept of size with the concept of quantity; that is, we may express sizes using numbers. In the discrete case this is just counting, in the continuous case this is measuring.
Measure consists in the superposition of the magnitudes to be compared; it therefore requires a means of using one magnitude as the standard for another. In the absence of this, two magnitudes can only be compared when one is a part of the other; in which case also we can only determine the more or less and not the how much.
I think I read this bit a little differently from @StreetlightX, but our two accounts are complementary rather than opposed. I'm imagining something like the norm of a vector in a vector space. So a norm in a vector space (roughly) is a function that takes the vector to number which represents its length. The usual norm we have in Euclidean spaces is Pythagoras' theorem. If we have the point (3,4), 3 along 4 up in the plane, the distance it is from the origin is the hypotenuse of the triangle:
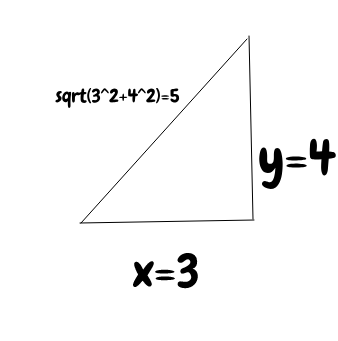
What this sets up is an embedding of position notions in the plane to position notions on the number line. IE, we have 'superposed' positions (magnitudes) in the plane (x=3,y=4) by taking them both as arguments of a function (f(x,y)=sqrt(x^2+y^2) with x=3, y=4) and used this function to map the position in the plane to a position on the line (sqrt(3^2+4^2)=sqrt(9+16)=sqrt(25)=5), which is then treated as a quantity that expresses the size (magnitude) of the position in the plane. In the absence of such an idea, a metric - a means of measurement -, we can only compare relative sizes through subset relations, such as (-----) being shorter than (-----------), which moreover is achieved without the explicit ascription of quantity.
However, note that this metric requires some kind of coordinate system - a means of expressing positions in terms of quantities -, and Riemann emphasises that we should instead consider the notion of coordinate system as conditioned by/associated with the objects (manifoldnesses/manifolds) whose points are commensurable under them. As he puts it:
The researches which can in this case be instituted about them form a general division of the science of magnitude in which magnitudes are regarded not as existing independently of position and not as expressible in terms of a unit, but as regions in a manifoldness.
What this does to the above idea of 'metric' is that it requires that such metrics, systems of measure on manifolds, become localised and indexed to the local topography of the manifold itself. This is a historical antecedent to condition (1) here, emphasising that systems of measure (coordinate systems and 'superpositions' like metrics) need only obtain locally on a manifold.
Such researches have become a necessity for many parts of mathematics, e.g., for the treatment of many-valued analytical functions; and the want of them is no doubt a chief cause why the celebrated theorem of Abel and the achievements of Lagrange, Pfaff, Jacobi for the general theory of differential equations, have so long remained unfruitful.
In terms of Riemann's argument, this is one of those bits of fluff that you'd send in a research grant application. It's just saying that the inquiry Riemann will do has practical consequences for maths. Riemann then provides an orienting, preparatory remark for §2 in which he'll describe multiply extended magnitudes consistent with the concerns in §1.
Out of this general part of the science of extended magnitude in which nothing is assumed but what is contained in the notion of it, it will suffice for the present purpose to bring into prominence two points; the first of which relates to the construction of the notion of a multiply extended manifoldness, the second relates to the reduction of determinations of place in a given manifoldness to determinations of quantity, and will make clear the true character of an n-fold extent.
Which states the research objective of treating manifolds as spaces unto themselves, but nevertheless finding systems of measurement that express their local topography. Moreover, he'll deal with the 'general case' of 'multiple extension', when we have as many directions of extension (dimensions/independent directions of variation) as we require. For example, 2 for the surface of a sphere despite it being in 3-space.
Welcome to The Philosophy Forum!
Get involved in philosophical discussions about knowledge, truth, language, consciousness, science, politics, religion, logic and mathematics, art, history, and lots more. No ads, no clutter, and very little agreement — just fascinating conversations.
Categories
- Guest category
- Phil. Writing Challenge - June 2025
- The Lounge
- General Philosophy
- Metaphysics & Epistemology
- Philosophy of Mind
- Ethics
- Political Philosophy
- Philosophy of Art
- Logic & Philosophy of Mathematics
- Philosophy of Religion
- Philosophy of Science
- Philosophy of Language
- Interesting Stuff
- Politics and Current Affairs
- Humanities and Social Sciences
- Science and Technology
- Non-English Discussion
- German Discussion
- Spanish Discussion
- Learning Centre
- Resources
- Books and Papers
- Reading groups
- Questions
- Guest Speakers
- David Pearce
- Massimo Pigliucci
- Debates
- Debate Proposals
- Debate Discussion
- Feedback
- Article submissions
- About TPF
- Help
More Discussions
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum