-
 unenlightened
10kIf the correct answer is 25%, then the correct answer is 50%.
unenlightened
10kIf the correct answer is 25%, then the correct answer is 50%.
If the correct answer is 50% or 60% then the correct answer is 25%
Therefore, the correct answer is 0% which is correct because it is not a choice on offer. If one could choose it, randomly or deliberately, it would be wrong. It's an amusing self-referential paradox, but I don't see anything special about it. It would have been more amusing, and neater, if one of the options (C) had been 0%
One expects there to be a right answer on offer, but there may not be.
2 + 2 = ?
A) 3
B) 203
C) 42
D) 8.73
Expect to get low marks in such tests, however hard you revise. -
 noAxioms
1.7k
noAxioms
1.7k
But there is. It asks about the odds of guessing correctly.There's no criterion for correctness, so there's no possible answer. — StreetlightX
I agree, and the consistency of this makes it not a paradox. Choice C should probably have been 0% instead of 60%. Then it would be a paradox I think.Therefore, the correct answer is 0% which is correct because it is not a choice on offer. — unenlightened -
TheMadFool
13.8kI don't get it.
There are only 3 choices 25%, 50% and 60%.
Random selection would be a chance of 1/3=33.33%. -
 Streetlight
9.1kIt asks about the odds of guessing correctly. — noAxioms
Streetlight
9.1kIt asks about the odds of guessing correctly. — noAxioms
Guessing what correctly though? Guessing the answer yes, but... to what? The question... which is... about the odds of guessing correctly. It's a weird little circle.
The self-reference of the indexical 'this' hides the fact that there is no actual question to which a chance of answering corresponds.
The two 25%s are a trick, a distraction. The question is unanswerable from the very beginning. -
 noAxioms
1.7k
noAxioms
1.7k
of correctly guessing the answer giving the correct odds.Guessing what correctly though? — StreetlightX
Yes, circular, but that doesn't mean there's no actual question. -
 Streetlight
9.1kOnce circularity is admitted, the game is up. The question is a verbal Penrose staircase:
Streetlight
9.1kOnce circularity is admitted, the game is up. The question is a verbal Penrose staircase:
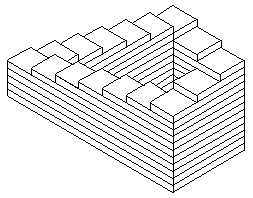
-
 Jeremiah
1.5k
Jeremiah
1.5k
There are four possible outcomes. That part never changes. The fact that two of the possible outcomes contain the same values does not change that there are four possible outcomes. We just increase our chances of being correct if the desired outcome is 25% since it is two of the four possible outcomes. -
 Jeremiah
1.5k
Jeremiah
1.5k -
 noAxioms
1.7k
noAxioms
1.7k
Of course it is circular. Perhaps there is a paradox that is not, but I cannot think of one offhand.The problem as I see is that the outcome changes the solution and I not sure if I would consider that truly circular. — Jeremiah
The question concerns the answer to the question. That's a circle, or more formally, self-referential.
You ask about the odds of correctly guessing the answer giving the correct odds of correctly guessing the answer giving the correct odds of correctly guessing the answer giving the correct odds of correctly guessing the answer ....
If none of the choices is correct, then the correct answer is simply not among the choices. 0% is the answer since it cannot be chosen. This itself is not paradoxical. Hence my comment that (C) should have been 0%, not 60. That forces the paradox.0% is not a possible outcome, which means there is a 0% chance of it being 0%. — Jeremiah -
 Jeremiah
1.5k
Jeremiah
1.5k
0% is not a possible outcome for the answer, therefore it cannot be chosen. Furthermore you are not wrong until after the chance event.
The idea that is it circular is just your perspective. There is a single chance event, one and only one. That is not a circle.
I considered the 0% version before making this thread, it really makes no difference at all as C is nothing but filler to give us four possible outcomes. The only reason to use the 0% version is to end moot arguments about how multiple choice questions work.
Also odds are not the same thing as chance. -
 noAxioms
1.7k
noAxioms
1.7k
????There is only one purposed chance event. It does not loop back on itself, it is not a circle and, as long as you don't say C), then you are not wrong until after the chance event, only then can you be wrong. — Jeremiah
You're wrong no matter what you choose. There is thus zero percent chance of choosing correctly, which is what the question asks. That the thing is self-referential doesn't seem to change that. It's not a paradox as written. -
 Streetlight
9.1kHow many letters does the correct answer have?
Streetlight
9.1kHow many letters does the correct answer have?
two
three
four
five — noAxioms
This too is unanswerable. -
 Jeremiah
1.5k
Jeremiah
1.5k
OK I'll try this one more time then that is it, as you don't seem to even comprehend what I am saying at all. Disagreeing is one thing, but not comprehending all together is quite another.
I fully understand what you are saying, that no matter what you pick you'll be wrong, but this is not an essay question where you get to put in your own answers, this is a multiple-choice question and you can only select from the available options and 0% is not in those available options, so it cannot be selected. If you can't understand that simple concept then you are not worth anymore of my time.
And the only reason you saw this as a circle is the same reason humans tend to think of time as linear, that is how your brain is processing the information, but it is not a circle. -
 VagabondSpectre
1.9k
VagabondSpectre
1.9k
The main problem is that "this question" grammatically and conceptually must refer to the multiple choice group (without any given criterion pointing to "correctness") or else it is a circular question.
The correct solution is your response + 1. What is your response?: the self-referential or recursive nature of this question makes it impossible to answer correctly.
If we presume that the question is not self referential then it seems answerable. And it is 33%. -
 Streetlight
9.1kYet another way to think about it is that the OP asks a meta-level question about an object-level question that is missing... rendering the meta-level question unanswerable.
Streetlight
9.1kYet another way to think about it is that the OP asks a meta-level question about an object-level question that is missing... rendering the meta-level question unanswerable.
I like puzzles like these. -
 Akanthinos
1kYet another way to think about it is that the OP asks a meta-level question about an object-level question that is missing... rendering the meta-level question unanswerable. — StreetlightX
Akanthinos
1kYet another way to think about it is that the OP asks a meta-level question about an object-level question that is missing... rendering the meta-level question unanswerable. — StreetlightX
This is it.
I'm not so sure this works as a conundrum, since it is literally impossible to answer correctly, but not based on the problem itself, but because of the answers offered as a limited horizon.
A conundrum's difficulty is in it's riddle, in finding a satisfying answer despite difficult conditions. -
 Caldwell
1.3kAlso odds are not the same thing as chance. — Jeremiah
Caldwell
1.3kAlso odds are not the same thing as chance. — Jeremiah
In that case @TheMadFool and @VagabondSpectre are correct. :smile:
Here's why. This is not marble-picking. This is choosing a unique answer from among the choices of four. There are only 3 unique answers, as two are the same. -
 Jeremiah
1.5k
Jeremiah
1.5k
Actually, there are four choices A, B, C and D. I get what they are driving at but the chance event is for four slots, which mean if we just look at the three values then 25 is 1/2 and 50 is 1/4 and 60 is 1/4. Saying they each have a 33% chance is suggesting they all have the same probability of being chosen by the chance event, which is not true; 25 has double the chance of being selected than the other values.
Furthermore just as 0% is not a selectable option neither is 33%. -
 Jeremiah
1.5kI am glad you like it, I plan on posting more math conundrums. I feel that even if they can't be answered we can still learn from them.
Jeremiah
1.5kI am glad you like it, I plan on posting more math conundrums. I feel that even if they can't be answered we can still learn from them. -
Fool
66Fun exercise. Here’s how I experienced it.
*read*
“Hm. Multiple choice random accuracy is 1/p for p choices, so the correct answer to this question is 1/p.”
“Oh, but 1/p shows up twice. More accurately, it’s 1/(degrees of freedom). If you know the full list of answers and you’ve picked 3, then you know what the 4th one is before you look at it, so it’s 1/(p-1)=1/3.”
“So the answer to this particular question is 1/3. But wait, no 1/3. This question’s correct answer is not listed, so there’s no chance of picking it. But wait, looks like 0% is actually the correct answer. Also not listed. The probability is still 0.”
“They tried to get me with the two 25%, tempting me to think the answer is 2*25%=50%, but that’s assuming the repeated answer choice doesn’t affect the odds. As an exercise in probability, it’s def 1/3, because we are picking at random and without assumptions about the meaning of the question. Strangely, I did have to know the meaning of the question in order to know the answer wasn’t listed, but now I’m just clarifying. My psychology does not affect the structure of the question.”
“If 0% were listed (once) alongside the two 25%, you would indeed go in circles. Finding no ‘1/3’, you revise to 0. Seeing 0 once, you revise again. Now thought processes divide. The meta view returns to 1/3, alternating with 0. The semantic view alternates between 1/2 and 1/4.”
“Does the fact that 25% is repeated change the odds? That’s double the risk of picking an answer that’s only 33% likely to be right. Well, no. The weighted average is still 33% because each hoice, being one of the three possible answers, has a 1/3 chance of winning.”
Very pleasant. Thank you. -
TheMadFool
13.8kThere are four possible outcomes. That part never changes. The fact that two of the possible outcomes contain the same values does not change that there are four possible outcomes. We just increase our chances of being correct if the desired outcome is 25% since it is two of the four possible outcomes. — Jeremiah
Thanks for clarifying. What I think is...
When we calculate the probability and say we have 50% chance of it being 25% we are assuming A)25% is the same as B)25%. But when we say if the correct answer is 50% or 60% then the probability is 25% we're making a distinction between A)25% and D)25%.
Seems like the fallacy of equivocation to me.
An example might help to clarify...
Scenario 1: we have 4 balls: 1 red, 1 green, 1 blue and 1 pink. I've chosen one ball.
The probability of you guessing my ball is a uniform 1/4 = 25%.
Scenario 2: there are 4 balls: 2 red, 1 green and 1 blue.
I've chosen a ball. What is the probability that you'll guess correctly.
You'll say 50% chance if it's red and 25% chance if it's non-red. Notice however that when yoy say 50% chance if it's red you're saying the two red balls are same. However when you say 25% chance that if it's non-red you're making a distinction between the two red balls. This is a fallacy. -
 Jeremiah
1.5k
Jeremiah
1.5k
That does not follow. Green and blue are both non-red so you add their probability together. Hey you don't have to believe me as this is basic math, just look it up. -
 Jeremiah
1.5kIt is not 33%, at all. That is just bad math. You can't combine similar values into one slot, as then you are no longer representing their proportion in the range of possible outcomes.
Jeremiah
1.5kIt is not 33%, at all. That is just bad math. You can't combine similar values into one slot, as then you are no longer representing their proportion in the range of possible outcomes.
Let me give a clear example of what I mean.
You have 5 beads 4 of them are blue and one of them is green. If one is selected at random then you have a 4/5 chance of getting a blue and a 1/5 chance of getting a green. You can't group all the blue beads into one bead and claim you have a 1/2 chance of getting a blue and a 1/2 chance of getting a green as then you are no longer accounting for the fact that there are 4 blue and only one green.
Welcome to The Philosophy Forum!
Get involved in philosophical discussions about knowledge, truth, language, consciousness, science, politics, religion, logic and mathematics, art, history, and lots more. No ads, no clutter, and very little agreement — just fascinating conversations.
Categories
- Guest category
- Phil. Writing Challenge - June 2025
- The Lounge
- General Philosophy
- Metaphysics & Epistemology
- Philosophy of Mind
- Ethics
- Political Philosophy
- Philosophy of Art
- Logic & Philosophy of Mathematics
- Philosophy of Religion
- Philosophy of Science
- Philosophy of Language
- Interesting Stuff
- Politics and Current Affairs
- Humanities and Social Sciences
- Science and Technology
- Non-English Discussion
- German Discussion
- Spanish Discussion
- Learning Centre
- Resources
- Books and Papers
- Reading groups
- Questions
- Guest Speakers
- David Pearce
- Massimo Pigliucci
- Debates
- Debate Proposals
- Debate Discussion
- Feedback
- Article submissions
- About TPF
- Help
More Discussions
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum






