-
 Count Timothy von Icarus
4.3k
Count Timothy von Icarus
4.3k
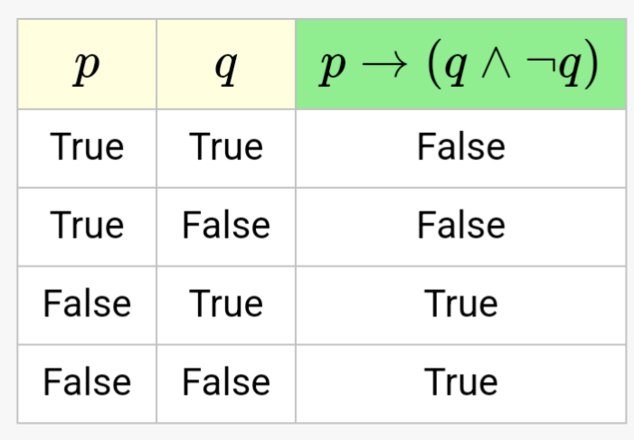
I don't think there is any mystery around (A→(B∧¬B)) |= ¬A, if something implies a contradiction we may say it is false. My curiosity was more around ¬(A→(B∧¬B)). We know that ¬(A→(B∧¬B))↔A is valid, (A→(B∧¬B)) entails ¬A, and ¬(A→(B∧¬B)) entails A. Tones gave a translation of the latter as:
"It is not the case that if A then B & ~B
implies
A"
I still can't make sense of it.
These are just paradoxes of material implication, no?
The negation of a contradiction is always true, and being true it is implied by anything, true or false.
As I noted earlier in response to Tones' reductio, a reductio is an indirect proof which is not valid in the same way that direct proofs are. You can see this by examining your conclusion. In your conclusion you rejected assumption (2) instead of assumption (1). Why did you do that?
Same here, it seems to me to be a paradox of material implication that is the source of confusion.
In a normal conversation, we might ask "but what if A really only implies B and not B and not-B?" Or conversely: "what if A only implies not-B but does not actually imply B?" But the way implication works here it is not an additional premise we can reject, we don't assign a truth value to it except in virtue of the truth values of A and B themselves.
If A is true then B always implies it, whether B is true or false.
In a relevance logic or per Aristotle's comments, we might turn around and question if A truly implies either B or not-B regardless of the truth value of either A or B alone.
For example, we could set up something like:
Elvis is a man - A
Elvis is a man implies that Elvis is both mortal and not-mortal. - A → (B and ~B)
Therefore Elvis is not a man.
Obviously, the common sense thing to do would be to reject "Elvis is a man implies Elvis is non-mortal," while affirming that "Elvis is a man does imply Elvis is mortal."
A truth table won't lay those possibilities out, it will only tell us how things work in terms of A or B being true.
However, there is a quite good reason not to do this in symbolic logic. Once you start getting into "what 'really' entails what," you get into judgement calls and a simple mechanical process won't be able to handle these.
But of course, you still need judgement to make sure your statements aren't nonsense, so you just kick that problem back a level. A proof from contradiction is only going to be convincing if we believe that A really does imply both B and not-B. I know plenty of skepticism has been raised against proofs from contradiction in general, outside of this issue, but for many uses they seem pretty unobjectionable to me. -
 Leontiskos
5.6kWhere — Lionino
Leontiskos
5.6kWhere — Lionino
Here:
1. A→(B∧¬B) assumption
2. A assumption
3. B∧¬B 1,2, conditional proof
4. ~A 2, 3 reductio — Banno
A reductio is not truth-functional. If we want to stick to strict truth functionality then we cannot accept reductios. In that case we can only think of them as indicating the inconsistency of a system, not as grounds for denying one thing or another. Technically a reductio is a form of special pleading (i.e. “Please let me reject this premise rather than that one, for no particular reason”). I think I can only be wrong about this if there is some principled difference between a supposition and a premise (or an assumption). A reductio is a kind of bridge between formal logic and the real world, and this is because of the background conditions it presupposes. In a purely formal sense no proposition is inherently more or less plausible than another, and therefore there is no reason to reject one premise rather than another in the event of a contradiction. -
 sime
1.2kThe main problem for me is, why can we read a→(b∧¬b) as "a implies a contradiction" but not ¬(a→(b∧¬b)) as "a does not imply a contradiction? — Lionino
sime
1.2kThe main problem for me is, why can we read a→(b∧¬b) as "a implies a contradiction" but not ¬(a→(b∧¬b)) as "a does not imply a contradiction? — Lionino
In general, the consistency of an axiomatic system isn't provable in an absolute sense due to Godel's second incompleteness theorem; the upshot being that consistency is a structural property of the entire system that isn't represented as a theorem by the system if it is sufficiently powerful.
Suppose that the logic concerned is weaker than Peano arithmetic, such that it can prove its own consistency. Then in this case, a proof of ¬¬a metalogically implies that ¬a isn't provable, i.e that a does not imply a contradiction.
But if the axiomatic system contains Peano arithmetic such that the second incompleteness theorem holds, then a proof of ¬¬a does not necessarily imply the absence of a proof of ¬a, since Peano arithmetic cannot prove its own consistency. -
 Leontiskos
5.6kThe negation of a contradiction is always true, and being true it is implied by anything, true or false. — Count Timothy von Icarus
Leontiskos
5.6kThe negation of a contradiction is always true, and being true it is implied by anything, true or false. — Count Timothy von Icarus
Yes, good. :up: Kreeft's point comes back.
In a normal conversation, we might ask "but what if A really only implies B and not B and not-B?" Or conversely: "what if A only implies not-B but does not actually imply B?" But the way implication works here it is not an additional premise we can reject, we don't assign a truth value to it except in virtue of the truth values of A and B themselves. — Count Timothy von Icarus
Right. As I have been saying it, "falsity incarnate" and "truth incarnate" are reifications. <FALSE> is a new idea, more or less foreign to classical logic.
However, there is a quite good reason not to do this in symbolic logic. Once you start getting into "what 'really' entails what," you get into judgement calls and a simple mechanical process won't be able to handle these. — Count Timothy von Icarus
Yep.
But of course, you still need judgement to make sure your statements aren't nonsense, so you just kick that problem back a level. A proof from contradiction is only going to be convincing if we believe that A really does imply both B and not-B. I know plenty of skepticism has been raised against proofs from contradiction in general, outside of this issue, but for many uses they seem pretty unobjectionable to me. — Count Timothy von Icarus
I think metabasis is useful, but I don't close my eyes to the fact that it is metabasis:
Every time we make an inference on the basis of a contradiction a metabasis eis allo genos occurs (i.e. the sphere of discourse shifts in such a way that the demonstrative validity of the inference is precluded). Usually inferences made on the basis of a contradiction are not made on the basis of a contradiction “contained within the interior logical flow” of an argument. Or in other words, the metabasis is usually acknowledged to be a metabasis. As an example, when we posit some claim and then show that a contradiction would follow, we treat that contradiction as an outer bound on the logical system. We do not incorporate it into the inferential structure and continue arguing. Hence the fact that it is a special kind of move when we say, “Contradiction; Reject the supposition.” In a formal sense this move aims to ferret out an inconsistency, but however it is conceived, it ends up going beyond the internal workings of the inferential system (i.e. it is a form of metabasis). — Leontiskos
Reductio ad absurdum is useful and important, but it is not formally valid in the same way that direct proofs are (and because of this it is a (useful) metabasis). We need to recognize that we are doing something special with a reductio, and that a reductio-inference to ¬A is quite different from a direct inference to ¬A. So if someone wants to say that ¬A is implied they must put an asterisk next to implied*. -
 Leontiskos
5.6kSuppose that the logic concerned is weaker than Peano arithmetic, such that it can prove its own consistency. Then in this case, a proof of ¬¬a metalogically implies that ¬a isn't provable, i.e that a does not imply a contradiction.
Leontiskos
5.6kSuppose that the logic concerned is weaker than Peano arithmetic, such that it can prove its own consistency. Then in this case, a proof of ¬¬a metalogically implies that ¬a isn't provable, i.e that a does not imply a contradiction.
But if the axiomatic system contains Peano arithmetic such that the second incompleteness theorem holds, then a proof of ¬¬a does not necessarily imply the absence of a proof of ¬a, since Peano arithmetic cannot prove its own consistency. — sime
Thanks. This is what I was trying to remember but could not find online (i.e. the complexities surrounding proofs of ¬¬a). -
 Leontiskos
5.6kThe main problem for me is, why can we read a→(b∧¬b) as "a implies a contradiction" but not ¬(a→(b∧¬b)) as "a does not imply a contradiction? — Lionino
Leontiskos
5.6kThe main problem for me is, why can we read a→(b∧¬b) as "a implies a contradiction" but not ¬(a→(b∧¬b)) as "a does not imply a contradiction? — Lionino
Are you interpreting "a does not imply a contradiction" as the basis of a reductio (i.e. "Suppose a; a implies a contradiction; reject a")? If so, then I again think it is because a reductio is not reducible to a truth-functional move. A reductio requires more than negation and falsity.
Edit:
I think I finally solved my own problem. When translating it to natural language, I was misplacing the associativity of the → operator.
So ¬(A → (B∧ ¬B)) is the same as (¬A) → (B∧ ¬B) — Lionino
Does this support my claim that what is at stake is something other than a material conditional? The negation does not distribute to a material conditional in the way you are now distributing it. -
 flannel jesus
2.9kI was misplacing the associativity of the → operator.
flannel jesus
2.9kI was misplacing the associativity of the → operator.
So ¬(A → (B∧ ¬B)) is the same as (¬A) → (B∧ ¬B) — Lionino
Do you believe for, for all statements (A -> B), you can do ¬(A -> B) and transform that into ¬A -> B? -
 flannel jesus
2.9k¬(A → B) is the same thing as ¬A→B — Lionino
flannel jesus
2.9k¬(A → B) is the same thing as ¬A→B — Lionino
That's what I was asking, thank you.
I don't believe that's correct. -
 flannel jesus
2.9kunderstand that you'd think that B∧¬B should be able to be replaced by any proposition P — Lionino
flannel jesus
2.9kunderstand that you'd think that B∧¬B should be able to be replaced by any proposition P — Lionino
Me? You understand that I think that?
But what just happened is that you did that, and I told you it's incorrect... -
 flannel jesus
2.9kI never replied positively to the question — Lionino
flannel jesus
2.9kI never replied positively to the question — Lionino
Well you gave what certainly looked like an affirmation. If I ask you "is lemonade your favourite flavour", and you say "lemonade is the same as my favourite flavour", most people are gonna think that's pretty much a "yes" to the question. -
 flannel jesus
2.9kIt is like 2(x*y)=2x*y, but 2(x*y)≠x*2y — Lionino
flannel jesus
2.9kIt is like 2(x*y)=2x*y, but 2(x*y)≠x*2y — Lionino
Is * multiplication here? I don't think this is right either. -
 flannel jesus
2.9k
flannel jesus
2.9k -
 javra
3.2kThe very proposition of "there both a) is a self and b) is no self" has (a) and (b) addressing the exact same thing - irrespective of how the term "self" might be defined or understood as a concept, the exact same identity is addressed — javra
javra
3.2kThe very proposition of "there both a) is a self and b) is no self" has (a) and (b) addressing the exact same thing - irrespective of how the term "self" might be defined or understood as a concept, the exact same identity is addressed — javra
The point is that if there is no determinate entity that 'the self' refers to, if there is only the concept, and if there is no actual entity, then saying that we are speaking about the same thing is incoherent. On the other hand, if you stipulate that the self is, for example, the body, then what would A be in the proposition (A implies B) where B is 'there is a self' ? Let's say that A is 'the perception of the body': this would be 'the perception of the body implies that there is a self". 'The perception of the body implies that there is no self' would then be a contradiction to that. — Janus
I’ll offer that the commonsense notion of “self” necessarily pivots around what we westerners commonly term “consciousness” - "the self" here always entailing the subject of one’s own experience of phenomena (or, in for example the more philosophical jargon of Kant, the “empirical ego” (via which empirical knowledge is possible) - this as contrasted to what he specifies as the underlying “transcendental ego”). And, in this commonsense understanding of "the self", the body of which one is aware is then not the “self” which is in question - "the self" instead holding as referent that which is so aware. Nor does the notion you present in any way cohere with the descriptions of self as they are addressed in the Buddhist doctrine of anatta: this being the very metaphysical understanding of reality from which we obtain propositions along the lines of “neither is there a self nor is there not a self”. Which, on the surface, do at least at first appear to be contradictory (though, as I've previously argued, do not need to so necessarily be).
But, since, we each hold our own - sometimes more divergent than at other times - understandings of what terms signify, I’ll here say that were the term “self” to be devoid of any referent outside of the occurrence of empirically observable physical bodies (maybe needless to add, that are living and so normally endowed with a subject of awareness, this rather than being dead and decaying), then I might find agreement with your general reasoning here.
I’m however not one to find the term “self” - and, hence, terms such as “I”, “you”, “us” and “them” - devoid of referents, unempirical (imperceivable) though I take these referents as "subjects of experience" to be. All the same, this thread is not the place to engage in debates regarding what “the subject of one’s own experiences” might specify or else be - although I do agree that it is not "an entity" in the sense of being a thing. -
 flannel jesus
2.9kIt is like 2(x*y)=2x*y, but 2(x*y)≠x*2y — Lionino
flannel jesus
2.9kIt is like 2(x*y)=2x*y, but 2(x*y)≠x*2y — Lionino
This doesn't make sense if * is "any operator" either. Replace * with + and 2(x*y)=2x*y is not true -
 flannel jesus
2.9kdidn't, you are referring to this ↪Lionino, which I already said was a copypaste mistake, it has been edited. I don't see what the issue is. — Lionino
flannel jesus
2.9kdidn't, you are referring to this ↪Lionino, which I already said was a copypaste mistake, it has been edited. I don't see what the issue is. — Lionino
The issue is you said you never wrote it, but you did write it. I understand it's a mistake. Therefore it's not correct to say you never wrote it, it's correct to say you wrote it by mistake.
"Any operator" is not any mathematical operator you want. — Lionino
I don't know the rules of that game, my bad
Welcome to The Philosophy Forum!
Get involved in philosophical discussions about knowledge, truth, language, consciousness, science, politics, religion, logic and mathematics, art, history, and lots more. No ads, no clutter, and very little agreement — just fascinating conversations.
Categories
- Guest category
- Phil. Writing Challenge - June 2025
- The Lounge
- General Philosophy
- Metaphysics & Epistemology
- Philosophy of Mind
- Ethics
- Political Philosophy
- Philosophy of Art
- Logic & Philosophy of Mathematics
- Philosophy of Religion
- Philosophy of Science
- Philosophy of Language
- Interesting Stuff
- Politics and Current Affairs
- Humanities and Social Sciences
- Science and Technology
- Non-English Discussion
- German Discussion
- Spanish Discussion
- Learning Centre
- Resources
- Books and Papers
- Reading groups
- Questions
- Guest Speakers
- David Pearce
- Massimo Pigliucci
- Debates
- Debate Proposals
- Debate Discussion
- Feedback
- Article submissions
- About TPF
- Help
More Discussions
- Panpsychism implies that computers are sacred expressions of human potential
- What's up with people who contradict themselves on their own sincerity & can't see their own faults?
- Why special relativity does not contradict with general philosophy?
- How "free will is an illusion" does not contradict theology
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum






