-
 Wayfarer
26.1kCouldn’t a logicist also be a nominalist? — Lionino
Wayfarer
26.1kCouldn’t a logicist also be a nominalist? — Lionino
That is one very deep and dense OP. I'll acknowledge that I'm not a mathematician and that many of the concepts you're discussing are beyond me. I think, of the above, what makes sense to me is intuitionism.
I've become interested in the topic because of the argument that numbers are real but not material, which is an embarrasment to most typical forms of contemporary naturalism, which is dogmatically physicalist. For example:
What is Benacerraf's problem? Perhaps the main problem for mathematical platonism, or lower-case platonism in general, is, if numbers are causally inert objects, how could it be that we have any knowledge of them, given we don't interact with them at all? — Lionino
It's not a problem for platonism, but a problem for naturalistic or empiricist accounts of knowledge. The question is, how can we know numbers, if they are purely intelligible in nature?
There's another article on this topic, The Indispensability Argument in the Philosophy of Mathematics which also leads with Benecareff. It starts:
In his seminal 1973 paper, “Mathematical Truth,” Paul Benacerraf presented a problem facing all accounts of mathematical truth and knowledge. Standard readings of mathematical claims entail the existence of mathematical objects. But, our best epistemic theories seem to deny that knowledge of mathematical objects is possible.
So, what are these 'best epistemic theories' and why do they seem to deny such knowledge? Why, it's because:
Mathematical objects are in many ways unlike ordinary physical objects such as trees and cars. We learn about ordinary objects, at least in part, by using our senses. It is not obvious that we learn about mathematical objects this way.
Doesn't that simply amount to problem for empiricism, i.e. the view that knowledge is attained mainly through sense-perception? So if mathematical knowledge is hard to square with empiricism, then so much the worse for it, I would have thought, considering how 'indispensable' it actually is for science itself.
It goes on:
(Rationalist) philosophers claim that we have a special, non-sensory capacity for understanding mathematical truths, a rational insight arising from pure thought. But, the rationalist’s claims appear incompatible with an understanding of human beings as physical creatures whose capacities for learning are exhausted by our physical bodies.
So instead of questioning why it is we can understand numbers, how about interrogating the claim that we are, in fact, 'physical creatures whose capacities for learning are exhausted by our physical bodies?' Or is that such an important principle in our 'best epistemic theories' that it has to be saved at all costs? That seems the point of the sophistry of the 'indispensability argument'.
So perhaps the 'crisis' is actually a manifestation of a problem at the foundations of naturalism itself, but it's kind of an 'emperor's new mind' type of scenario where nobody wants to admit it. Philosophical dualism and mathematical platonism have no such difficulties. But as it is, and as your cited SEP article on Platonism in Philosophy of Mathematics says,
Mathematical platonism has considerable philosophical significance. If the view is true, it will put great pressure on the physicalist idea that reality is exhausted by the physical. For platonism entails that reality extends far beyond the physical world and includes objects that aren’t part of the causal and spatiotemporal order studied by the physical sciences.[1] Mathematical platonism, if true, will also put great pressure on many naturalistic theories of knowledge. For there is little doubt that we possess mathematical knowledge. The truth of mathematical platonism would therefore establish that we have knowledge of abstract (and thus causally inefficacious) objects. This would be an important discovery, which many naturalistic theories of knowledge would struggle to accommodate.
Oh, and as for the question I quoted - from my limited understanding, Frege, who had quite a bit to say about that, believed in the reality of abstract objects, which nominalism explicitly does not. See Frege on Knowing the Third Realm, Tyler Burge (public domain.) -
 Banno
30.6kGoodness.
Banno
30.6kGoodness.
A wonderful topic, but I suspect that there is too much here for a single thread - it might have been better to choose one part of the issue at a time to deal with. The juggler will have. a hard time working out which ball is which.
Despite that, I'd throw another ball to the juggler: Wittgenstein’s Philosophy of Mathematics
On Wittgenstein’s view, we invent mathematical calculi and we expand mathematics by calculation and proof, and though we learn from a proof that a theorem can be derived from axioms by means of certain rules in a particular way, it is not the case that this proof-path pre-exists our construction of it. -
 Metaphysician Undercover
14.8k
Metaphysician Undercover
14.8k
Good post, very informative.
Oh, and as for the question I quoted - from my limited understanding, Frege, who had quite a bit to say about that, believed in the reality of abstract objects, which nominalism explicitly does not. See Frege on Knowing the Third Realm, Tyler Burge (public domain.) — Wayfarer
I believe that what nominalism rejects is the idea that abstractions may be classed as "objects". So nominalism does not explicitly reject abstractions, it rejects "abstractions are objects".
If i remember correctly, the difference between nominalism and realism follows from a difference in interpretation of Aristotle's active intellect and passive intellect. Aristotle had determined that the intellect must consist of a passive aspect to receive forms from sense objects, and an active aspect to constrict conceptions beyond the limits of particular instances of sensation. Differences in how one "positions" these two aspects "within the world" result in the distinction between nominalism and realism.
Some thinkers wanted to maintain the intellect as pure separable Form, allowing that the intellect transcends the body in the immortality of the soul. That, I believe, is the realist position. This places the reality of the abstraction as non-spatial and within the intellect of the individual, but separable from the passive aspect which receives forms in sensation, and is attributed to the sense organs. Others assumed that the proper "active intellect" is already independent from the individual, as a feature of the collective 'people'. That, I believe, is the nominalist position. This makes the individual's intellect simply a passive intellect, receiving all it knows through sensation, passing that to the society where it becomes "knowledge" through justification.
You'll notice the nominalist representation is the more simple, at first glance, on the first level, dividing the passive intellect from the active through the two evident principles of 'property of individual', and 'property of the society'. It leaves a huge problem though, at a deeper level, as the reality of "the collective" the society, which must now be an entity with properties. The realist representation appears to be more complex because it exposes the problem of the duality of the intellect on the surface, as inherent within each individual intellect, instead of hiding it under the veil of an illusionary object "the collective".
The two render the "position" of the actual existence of the abstraction as fundamentally different. The realist places the abstraction as non-spatial, inside the fundamentally immaterial mind of the individual, while the nominalist places the actual existence of the abstraction as attributable to the society as a whole, and therefore independent from the individual mind. Therefore nominalism leaves the abstraction as a property of an object (the collective society) rather than as an object itself, while realism allows the abstraction to be a special type of object (non-spatial) which inheres within the minds of individuals.
Each has it's own problem. The nominalist has to validate the reality of "the collective", as an object, and the realist has to validate the reality of "the mind" as something within the individual, yet distinct from the physical body. -
 Count Timothy von Icarus
4.3k
Count Timothy von Icarus
4.3k
g. Max Tegmark's Mathematical Universe (a type of mathematical monism) includes the view that every possible mathematical structure exists. Would the Mathematical Universe of Max Tegmark then be a naturalised FBP?
It's worth noting that Tegmark justifies his view with the claim that it fixes the Fine Tuning Problem in physics. I do not think this actually works. Basically, if every possible universe exists, then we seem to run into all sorts of undetermination problems and issues that are somewhat akin to the Boltzman Brain problem, although different.
Apparently, my objection is not novel and someone pointed it out to Tegmark, although they did it by only focusing on the problem as respects non-computable mathematical objects. This caused Tegmark to revise the hypothesis such that only computable objects exist. Aside from seeming ad hoc though, I do not think this actually solves the problem of how the MUH is not a good solution to the Fine Tuning Problem.
It is, nonetheless, an interesting idea. I think it's worth pointing out that Tegmark's 3rd (or maybe 4th?) level multiverses are themselves mathematical objects, singular. That is, universes are not composed of multiple discrete mathematical objects, which makes them a bit different than some other forms of platonism/ontic-structural realism.
d. Conceptualism: really anti-realist? If we admit that the mind is part of reality, doesn’t research in mathematics equate with investigating our own minds? You might insist that it is still anti-realist because it’s not mind-independent, but the anti-realist label brings a connotation of fiction (not in the sense of fictionalist nominalism). In this case, the question is: does conceptualism really imply some sort of fiction (something we make up like stories, or perhaps useful stories like myths) or implies an investigation of our own minds as an object of study (cognitive science and psychology)? It seems to be the latter, given the fact that conceptualism turns mathematics into a branch of psychology.
Right, and if our minds produce such things, we might ask "why do they do so?" Trading off arguments made by enactivists, we can say that brains don't produce any consciousness in most environments. From development to death, there is a constant two-way flow of causes across any supposedly discrete barrier that constitutes a person. If we come to have mathematical intuitions and develop mathematical ideas, we do not do so in isolation, so how does this tie back to the world?
I can imagine all sorts of answers here, and many would not be anti-realist. IMO, it's really not that different from questions as to whether cats, trains, atoms, recessions, communism, etc. all really exist, if they are "mind-independent," etc.
My personal take would be that minds are somewhat unique in being able to use syntax to bring many properties of things together and make them phenomenologically "present" at once. However, this still represents a relation between things in the world, and is in no way a sort of "less real" relationship for involving phenomenal awareness. Indeed, I can see an argument for these relationships being "more real" in that the development of clear knowledge of "what a thing is," is itself the relation in which a thing "most essentially is what it is." In knowledge, many of a thing's properties come together at once, whereas normally any one thing is only manifesting some of its properties over any given interval.
c. Can a physicalist (or generally naturalists) be a platonist, or should they stick with nominalism or immanent realism? It seems they can't, because commitment to abstract objects seems to be a commitment to non-physical objects, but see for example naturalised platonism (3).
Naturalism seems generally to be defined loosely enough that I don't see an issue here. Consider Pinkhard's argument that Hegel is a naturalist for example. More broadly, it seems like there could be a naturalism that distinguishes between realms of being and becoming, existence/subsistance and actualization, actual and potential, etc., which might leave room for platonism.
Physicalism, if it's in the conventional package of "everything that exists is physical," superveniance, and causal closure seems more dicey unless a number of moves are made.
Gisin's application of intuitionism to physics adds an interesting wrinkle here, but I still think it might be consistent with a certain sort of naturalist platonism. If anything, it would seem to change physicalism more if it ever becomes mainstream.
Most physics theories are deterministic, with the notable exception of quantum mechanics which, however, comes plagued by the so-called measurement problem. This state of affairs might well be due to the inability of standard mathematics to "speak" of indeterminism, its inability to present us a worldview in which new information is created as time passes. In such a case, scientific determinism would only be an illusion due to the timeless mathematical language scientists use. To investigate this possibility it is necessary to develop an alternative mathematical language that is both powerful enough to allow scientists to compute predictions and compatible with indeterminism and the passage of time. We argue that intuitionistic mathematics provides such a language and we illustrate it in simple terms.
https://arxiv.org/abs/2011.02348 -
 Wayfarer
26.1kanother layer of explanation that this theory would require. — Lionino
Wayfarer
26.1kanother layer of explanation that this theory would require. — Lionino
I think the confusion revolves around the equivocation of the term 'object' in 'mathematical object'. Numbers are not actually objects in any sense but the allegorical. There is no object '2'. What there is, is the act of counting which is denoted by the symbol '2'.
Step back a little. You may recall an allegory that dates back to the 19th century, about how a two-dimensional surface of water would perceive a three-dimensional cone. Absent any idea of a third dimension, the surface could only ever perceive the cone in terms of concentric circles //and ellipses//. Then there'd be this big conceptual problem as to how all these circles are related. You could write an equation, presumably, that described the progression of circles, but you still wouldn't be seeing what they represent.
I think there's something analogous to that operating in this argument. The cone analogy is a metaphor for the limitations inherent in empiricist understanding (akin to pistis or doxa in Plato's terms), which cannot by itself grasp the sense in which mathematical knowledge is 'higher'. There is no higher! There's only the flatland of empirical reality mediated by physical senses. Just as the two-dimensional surface perceives only the cross-sections of a cone, without a conception of the three-dimensional object itself, empirical observation alone cannot fully comprehend the abstract realities that Platonists argue transcend physical particulars. This analogy underscores the empiricist critique of Platonism, suggesting that notions of 'higher' or 'abstract' truths, such as mathematical entities, are outside the domain of of empirical verification and as such cannot be explained in those terms.
And the diagram you provide illustrates the problem, as it's two-dimensional. I think that what happens in reality, is that rational inference (including counting) operates on a different level, but in concert with, sensory cognition (per Kant). Whereas the diagram seeks to treat them in the same way, that is, as objects, and then asks how they're related. It's a category problem, which ultimately originates in the 'flattening' of ontology that occurs with the transition to the modern world-view (hence the relevance of the 'flatland' argument.) Hence, it's a metaphysical problem, but as the proponents of empiricism are averse to metaphysics, they of course will not be able to acknowledge that.
The problem is still how that faculty works to understand mathematical truths. It seems no one has given a satisfactory explanation. — Lionino
Mathematics is what explains. We don't need to explain arithmetical primitives, they are what provides the basis of explanation. Trying to explain mathematics by reducing those faculties to the sensory is the source of the problem. -
 013zen
164While its a little antiquated, I think a good starting point is the manner in which Frege considered it in The Foundations of Arithmetic. Philosophers from Mill, to Kant, to Frege were wondering two things:
013zen
164While its a little antiquated, I think a good starting point is the manner in which Frege considered it in The Foundations of Arithmetic. Philosophers from Mill, to Kant, to Frege were wondering two things:
“Are mathematical statements analytic or synthetic?”
and
“Are mathematical statements a priori or a posteriori?
Empiricists/realists like Mill thought we learned the meanings of mathematical statements by generalizing from experience. They are a posteriori. We see things in different groupings, and we generalize from there.
Both Kant and Frege disagreed with Mill, both thought that we learn the meaning of mathematical statements without any recourse to reality. Frege, to put it simply thinks it would be bizarre to suppose that my understanding of the number:
“6915027410”
is in any sense based on my experiences. To what experiences could I possibly point? This is true of mostly any and all numbers and combinations of numbers you might suppose outside the first few small numbers.
Kant thought mathematical statements were synthetic a priori and Frege thought that mathematics was analytic a priori. This is an important distinction, because it sets up the difference between psychologism vs logicism; the latter which, like empiricists hold mathematical statements to be mind independent facts versus psychologism which holds them to be mind dependent.
Kant thought, for example, that in the proposition:
“4+2=6”
Kant said that nowhere in the idea of “4”, “2”, or “2+4” is the concept “6” found. In order to show this, consider the following proposition:
“38102465 – 91042 = 38011423”
It’s obvious, that the random number “38011423” is in no sense containing the other individual numbers: “38102465”, “91042”
Then how do we know this statement is true? Kant's answer was that the necessary content was supplied by the mind. By the pure concepts supplied by understanding.
Frege argued that Kant misunderstood what the distinction between analytic and synthetic rested on. It was not based on the content of proposition, or the individual term's meanings, but rather, it related to one’s justification for accepting the truth of the statement.
Frege agreed with Kant, that the number “6” did not contain “4” or “2” or any number that can be added or subtracted to equal “6”, but we none the less know analytically that “6” must be the result of “4+2” because whether or not a statement was analytic or synthetic was based on whether or not it could be defined.
Mathematical statements are true analytically because they are provable, according to Frege. So, even if humans all died out, or never existed, the “Pythagorean theorem” will always be provable. -
 Metaphysician Undercover
14.8kAnd the diagram you provide illustrates the problem, as it's two-dimensional. I think that what happens in reality, is that rational inference (including counting) operates on a different level, but in concert with, sensory cognition (per Kant). Whereas the diagram seeks to treat them in the same way, that is, as objects, and then asks how they're related. It's a category problem, which ultimately originates in the 'flattening' of ontology that occurs with the transition to the modern world-view (hence the relevance of the 'flatland' argument.) Hence, it's a metaphysical problem, but as the proponents of empiricism are averse to metaphysics, they of course will not be able to acknowledge that. — Wayfarer
Metaphysician Undercover
14.8kAnd the diagram you provide illustrates the problem, as it's two-dimensional. I think that what happens in reality, is that rational inference (including counting) operates on a different level, but in concert with, sensory cognition (per Kant). Whereas the diagram seeks to treat them in the same way, that is, as objects, and then asks how they're related. It's a category problem, which ultimately originates in the 'flattening' of ontology that occurs with the transition to the modern world-view (hence the relevance of the 'flatland' argument.) Hence, it's a metaphysical problem, but as the proponents of empiricism are averse to metaphysics, they of course will not be able to acknowledge that. — Wayfarer
It may be argued that the most fundamental use of numbers is in ordering, first second third, etc.. In this sense the number cannot be an object at all, but a place marker in a hierarchy or perhaps a temporal order. The hierarchy is a value structure, and it may be asked what it means to mark a position in such a structure. Even the question of what it means to mark a place in a temporal order is perplexing. -
 Count Timothy von Icarus
4.3kOf course you can also trace the emergence of quantity to contradictions inherit in sheer, indeterminate being :grin:
Count Timothy von Icarus
4.3kOf course you can also trace the emergence of quantity to contradictions inherit in sheer, indeterminate being :grin:
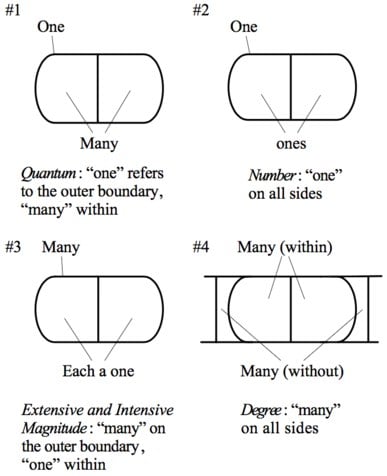
-
 Wayfarer
26.1kI recall an article about how geometry began in Egypt - obviously the construction of the Pyramids required advanced geometry but well before that it was used to allocate plots of farming land on the Nile delta. It will be recalled that this floods every year and the boundaries are erased, so every year the plots have to be allocated anew along the sides of the river-banks, which required sophisticated reckoning. The origins of arithmetic were likewise associated with the Babylonian-Sumerian culture - the ‘cradle of civilisation’ - for reckoning cattle numbers and storage of crops. You can see how arithmetic generally would be associated with ownership, building, cultivation of crops and conversely how it would not be of much relevance to hunter-gatherer cultures.
Wayfarer
26.1kI recall an article about how geometry began in Egypt - obviously the construction of the Pyramids required advanced geometry but well before that it was used to allocate plots of farming land on the Nile delta. It will be recalled that this floods every year and the boundaries are erased, so every year the plots have to be allocated anew along the sides of the river-banks, which required sophisticated reckoning. The origins of arithmetic were likewise associated with the Babylonian-Sumerian culture - the ‘cradle of civilisation’ - for reckoning cattle numbers and storage of crops. You can see how arithmetic generally would be associated with ownership, building, cultivation of crops and conversely how it would not be of much relevance to hunter-gatherer cultures. -
 Metaphysician Undercover
14.8kI recall an article about how geometry began in Egypt - obviously the construction of the Pyramids required advanced geometry but well before that it was used to allocate plots of farming land on the Nile delta. It will be recalled that this floods every year and the boundaries are erased, so every year the plots have to be allocated anew along the sides of the river-banks, which required sophisticated reckoning. — Wayfarer
Metaphysician Undercover
14.8kI recall an article about how geometry began in Egypt - obviously the construction of the Pyramids required advanced geometry but well before that it was used to allocate plots of farming land on the Nile delta. It will be recalled that this floods every year and the boundaries are erased, so every year the plots have to be allocated anew along the sides of the river-banks, which required sophisticated reckoning. — Wayfarer
Yes, I read similar information. I was researching the origins of the Pythagorean theorem, and "the right angle" and found that the general principle (probably the 3,4,5 triangle) was being used by the Egyptians to produce parallel lines for plots of land. In one of Plato's dialogues, in a sort of myth form, he talks about the movement of ideas from Egypt to what is now Italy. I believe it was part of Greece then.
The point I was making is that it may be the case that numbers first arose simply for the purpose of ordering, priority, before and after. Notice that when we learn to count, at a very young age, what we learn is an ordering of the symbols, count from one to ten for example. We learn to count (order the symbols) before learning about quantity. I believe this is why numbers are known as objects.
There is nothing else for the symbols to represent, because they do not represent a quantity of things. 1 is before 2, and 2 is before 3. To understand this meaning in terms of hierarchic priority, or even temporal priority would require very difficult conceptualization for a child learning how to count, so we simply say that "1" stands for a number, which is before the number represented by "2" etc., or "lower and higher". Employing these objects (numbers) allows us to avoid understanding what before and after, lower and higher, actually mean, leaving that to be determined by the context of application. The principal application became lower and higher quantity. So, by saying that the numeral represents an object (a number), and that the objects may be ordered, allows that "order" be left undefined, for unlimited applications.
But the object, the number itself is actually redundant. The symbol may directly represent the quantity or order of the application without the requirement of the object as a medium. The object was only employed to facilitate understanding the usage. So the idea that there is an object (a number) between the symbol and the thing which the symbol represents in usage, is a sort of self-deception. This self-deception becomes very misleading when it becomes an axiom of set theory. -
 Count Timothy von Icarus
4.3k
Count Timothy von Icarus
4.3k
The Stanford Encyclopedia article on Hegelian Dialectics, which is quite good too. I can see why people found similarities between Spencer Brown's "Laws of Form" and this. There is some interesting work on formalizing Hegel's Logic using category theory but it's sort of over my head. I would assume that if it can truly replicate the idea of can overcome many limits to formal systems in that contradiction is no longer an issue, but the very engine of changing the system itself.
There seems to be an interesting link between Hegel's Logic, Brown, information theory, and St. Denis/Eriugena I want to write about some day if I ever feel like I understand them well enough. -
 Corvus
4.8kReally? You must be a mathematician like I was. And one working in functional analysis. I have perhaps four books that speak of Hilbert spaces in certain chapters. — jgill
Corvus
4.8kReally? You must be a mathematician like I was. And one working in functional analysis. I have perhaps four books that speak of Hilbert spaces in certain chapters. — jgill
No I am not. :) I was trying to learn about it better. I kept getting more books on the topic until I find the best one. Ended up with about 10 of the books in the shelf. The last one I got was "Introduction to Hilbert Spaces with Applications" by Lokenath Debnath and Piotr Mikusinski 3rd Edition. It seems the best one so far. But the N. Young and Holland Jr. ones seem also good. -
 EricH
661First of all my complements on a very well constructed OP. Anyway, this is sort of a whimsical notion, but I'm seeing a sort of a poetic analogy between this and discussions of Quantum Physics. Just as a photon is either a wave or particle depending on how it is measured, it seems like these difference in math philosophy may all be neither wrong nor right - it depends on how the topic is approached.
EricH
661First of all my complements on a very well constructed OP. Anyway, this is sort of a whimsical notion, but I'm seeing a sort of a poetic analogy between this and discussions of Quantum Physics. Just as a photon is either a wave or particle depending on how it is measured, it seems like these difference in math philosophy may all be neither wrong nor right - it depends on how the topic is approached.
Don't take this too literally :roll: -
 jgill
4kOK, back unexpectedly quickly. What little I know of SOL is that it applies to set theory, and foundations wallows in that mire. I suspect if one wants to see how it translates into common mathematics one must start with 0={ }, and work up to sophisticated functions. I did this back in 1962 in my first grad math class. It was done on handout sheets, and we ended up defining the exponential function.
jgill
4kOK, back unexpectedly quickly. What little I know of SOL is that it applies to set theory, and foundations wallows in that mire. I suspect if one wants to see how it translates into common mathematics one must start with 0={ }, and work up to sophisticated functions. I did this back in 1962 in my first grad math class. It was done on handout sheets, and we ended up defining the exponential function.
It was entertaining at the time, but not at all useful to me or 97% of the class. One guy went ecstatic and followed this dream. The rest of sighed relief and moved on.
Functions from sets might help.
Oh, here is an example of a Hilbert space: A Hilbert space -
 Banno
30.6k
Banno
30.6k
Same here.It seems more reasonable to me than the inverse that mathematics was/is invented and that applications for it were/are discovered. — 180 Proof
Pretty much. So mathematical expressions are true only if there is a proof-path that shows it to be true. There are, one concludes, mathematical expressions that are neither true nor false. This is opposed to Platonism, in which mathematical expressions are either true or false regardless of our having a proof.When he says proof-path, is he referring to the syntax which we use to prove theorems? — Lionino
Arguably this approach is not subject to Benacerraf's problem because there need not be a thing to which each number refers.
Wittgenstein's own approach place restrictions on the creativity mathematicians.
But this topic requires a far more formal approach than is doable here.
Welcome to The Philosophy Forum!
Get involved in philosophical discussions about knowledge, truth, language, consciousness, science, politics, religion, logic and mathematics, art, history, and lots more. No ads, no clutter, and very little agreement — just fascinating conversations.
Categories
- Guest category
- Phil. Writing Challenge - June 2025
- The Lounge
- General Philosophy
- Metaphysics & Epistemology
- Philosophy of Mind
- Ethics
- Political Philosophy
- Philosophy of Art
- Logic & Philosophy of Mathematics
- Philosophy of Religion
- Philosophy of Science
- Philosophy of Language
- Interesting Stuff
- Politics and Current Affairs
- Humanities and Social Sciences
- Science and Technology
- Non-English Discussion
- German Discussion
- Spanish Discussion
- Learning Centre
- Resources
- Books and Papers
- Reading groups
- Questions
- Guest Speakers
- David Pearce
- Massimo Pigliucci
- Debates
- Debate Proposals
- Debate Discussion
- Feedback
- Article submissions
- About TPF
- Help
More Discussions
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum











