-
 wonderer1
2.4kThe velocity of the patch in contact with the ground is zero with respect to the ground, unless you've lost traction.
wonderer1
2.4kThe velocity of the patch in contact with the ground is zero with respect to the ground, unless you've lost traction.
Although only when looking at things kind of simplistically. Heisenberg's principle applies, whether you are looking close enough to notice or not. -
 Metaphysician Undercover
14.7kCircular motion is a very strange sort.
Metaphysician Undercover
14.7kCircular motion is a very strange sort.
The velocity of the patch in contact with the ground is zero with respect to the ground, unless you've lost traction. — wonderer1
Traction is often less than a hundred percent, so the motion of that point on the wheel, relative to the ground, would often be in the direction opposite to the intended direction of the vehicle. That produces unpredictability, making it so much fun to hit the gas pedal hard on a slick surface. -
 hypericin
2kInteresting, I never thought of this. But it is most definitely true.
hypericin
2kInteresting, I never thought of this. But it is most definitely true.
Now, which part of the wheel is moving twice the speed? I guess that would be the top of wheel. — Lionino
It is the point where the wheel's velocity wrt the ground is maximized. At every other point there is some vertical motion as well. -
 Agree-to-Disagree
674Neil de Grasse Tyson says that where the moving wheel touches the road, its speed is zero. True or false? — frank
Agree-to-Disagree
674Neil de Grasse Tyson says that where the moving wheel touches the road, its speed is zero. True or false? — frank
Hi Frank. This is a very interesting question.
The curve traced by a point on a circle as it rolls along a straight line without slipping is called a cycloid.
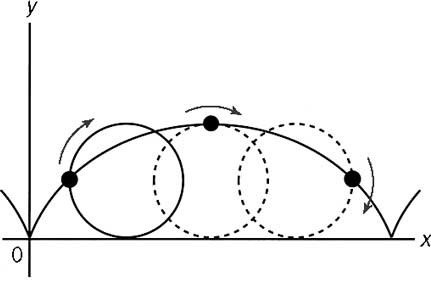

But the point where the moving wheel touches the road is not following the path of a cycloid. It is a point moving in a straight line at the same speed as the car is moving.
Imagine a car travelling at 10 meters per second. At time T = 0 the point in contact with the ground is at distance D = 0. One second later at time T = 1 the point in contact with the ground is at distance D = 10. It has moved at 10 meters per second, the same as the speed of the car.
Neil de Grasse Tyson is wrong. :scream: -
 noAxioms
1.7k
noAxioms
1.7k
All this is wrong. A point on the rim of a rigid not-slipping wheel IS folling the path of a cycloid (not well depicted in the drawing which shows the path coming in from an angle instead of vertically), and is very much is stationary relative to the road, not the car. The axle is moving at the speed of the car, and no point on the wheel is ever stationary relative to the axle while the car is moving.But the point where the moving wheel touches the road is not following the path of a cycloid. It is a point moving in a straight line at the same speed as the car is moving. — Agree-to-Disagree
Am I reading your comment wrong? It seems you're just asserting things that are obviously wrong.
The reason everyone gets it wrong is because the correct answer (4) isn't one of the options. It isn't because nobody can figure it out correctly. I've had that problem on a different test (not multiple choice) and got it right, as did a fair percentage of others.A thought problem along similar lines (or curves): "The SAT Question that Everyone Got Wrong" — wonderer1 -
 Agree-to-Disagree
674But the point where the moving wheel touches the road is not following the path of a cycloid. It is a point moving in a straight line at the same speed as the car is moving.
Agree-to-Disagree
674But the point where the moving wheel touches the road is not following the path of a cycloid. It is a point moving in a straight line at the same speed as the car is moving.
— Agree-to-Disagree
All this is wrong. A point on the rim of a rigid not-slipping wheel IS folling the path of a cycloid (not well depicted in the drawing which shows the path coming in from an angle instead of vertically), and is very much is stationary relative to the road, not the car. The axle is moving at the speed of the car, and no point on the wheel is ever stationary relative to the axle while the car is moving.
Am I reading your comment wrong? It seems you're just asserting things that are obviously wrong. — noAxioms
I will try to explain my reasoning.
A fixed point on the rim of a rigid not-slipping wheel does follow the path of a cycloid.
But the point where the moving wheel touches the road is not a fixed point on the rim of a rigid not-slipping wheel. The point where the moving wheel touches the road moves relative to a fixed point on the rim of a rigid not-slipping wheel. The point where the moving wheel touches the road moves around the rim as the wheel turns(i.e. it is not fixed).
That is why the point where the moving wheel touches the road is not following the path of a cycloid. It is a point moving in a straight line at the same speed as the car is moving. -
 jgill
4kThat is why the point where the moving wheel touches the road is not following the path of a cycloid. It is a point moving in a straight line at the same speed as the car is moving. — Agree-to-Disagree
jgill
4kThat is why the point where the moving wheel touches the road is not following the path of a cycloid. It is a point moving in a straight line at the same speed as the car is moving. — Agree-to-Disagree
I agree. The point under discussion is not a point on the wheel, more of a point on the road that moves with the movement of the vehicle. But whatever. -
 noAxioms
1.7k
noAxioms
1.7k
Ah, gotcha, and that made me re-read the way the OP was worded, and I think your take is more correct than the way I saw the question being asked.But the point where the moving wheel touches the road is not a fixed point on the rim — Agree-to-Disagree
Trying to figure out which starting assumption (unstated) would reach an one (but not all) the other answers. For instance, I could assume that circle B is rotating, or that circle A is slipping, but either assumption leads to any of the answers being possible.The answer varies with starting assumptions. — frank
I'm also from a physics background where rotation is absolute, not something that is frame dependent.
I didn't watch the video, so I'm just commenting on what is shown in the still shot. Surely the makers of the test selected one of the five answers as being 'correct', and surely somebody must have guess that selection, either in ignorance or in realizing that the correct answer isn't an option. The title suggests that this answer is selected by nobody, which is implausible.The video does explain that. — Wayfarer -
 Sir2u
3.6kNow, which part of the wheel is moving twice the speed? I guess that would be the top of wheel. — Lionino
Sir2u
3.6kNow, which part of the wheel is moving twice the speed? I guess that would be the top of wheel. — Lionino
Nope, that would be science fiction, the part at the top travels at the same speed.
The problem here I think is one of "in relation to what is the velocity measured".
Lets try looking at this from a slightly different point of view.
You are walking or running down the road at a certain speed. each time your foot touches the road it stays there for a certain time while the rest of your body moves forward.
From this point of view, de Grasse is correct. In that instant your point of contact with the road is not moving hence a velocity of zero. -
 Sir2u
3.6kIf you are considering linear speed, yes. If you are considering instantaneous speed in relation to the floor. — Lionino
Sir2u
3.6kIf you are considering linear speed, yes. If you are considering instantaneous speed in relation to the floor. — Lionino
I was just stating that I can find no way to explain how it would be possible for one point on the wheel's circumference to to be traveling at a different speed to another point on the circumference. That just cannot happen.
At the same instance that the patch is in contact with the road the top part of the wheel also has a velocity of zero as does every equivalent area on the wheel.
Not only is there speed that comes from the cars movement, but from the tire going around itself. — Lionino
But we can always add to that the speed of rotation of the earth, the speed of orbit of the earth, the speed of the sun orbiting the Milky Way.
But that goes way beyond the point de Grasse is trying to make. -
 Lionino
2.7kI was just stating that I can find no way to explain how it would be possible for one point on the wheel's circumference to to be traveling at a different speed to another point on the circumference. That just cannot happen. — Sir2u
Lionino
2.7kI was just stating that I can find no way to explain how it would be possible for one point on the wheel's circumference to to be traveling at a different speed to another point on the circumference. That just cannot happen. — Sir2u
The tire is spinning at the same speed as the car (v). The angular speed is v/r where r is the radius of the tire. That is how the car moves.
A point in the left or right side of the tire is not only moving at the same speed as the car, because the car is moving, but it is also going up or down. A point on the top is moving twice the speed of the car because not only is it part of the moving car, it is also spinning towards the direction of movement of the car, so it goes twice the speed in relation to the ground. A point on the bottom of the wheel is at speed 0 in relation to the floor because the speed of it spinning and the speed of the car cancel out, giving 0.
That is only about instantaneous speed.
But we can always add to that the speed of rotation of the earth, the speed of orbit of the earth, the speed of the sun orbiting the Milky Way. — Sir2u
We can't because it is completely irrelevant. -
 Sir2u
3.6kThat is only about instantaneous speed. — Lionino
Sir2u
3.6kThat is only about instantaneous speed. — Lionino
If the wheel has a circumference of 2 meters, the car will advance 2 meters for each rotation if there is no slippage. That is the rotational speed of the wheel in relation to linear velocity of the car. No part of the wheel can advance fast than the car. in fact at certain parts of the revolution all points around the circumference are traveling in the opposite direction to the car. Combining the speeds is not possible because they do not have the same vector.
Nothing you wrote in any way explains how any part of a wheel can travel faster than another part of it, which is what I asked you to explain. -
 Lionino
2.7kThanks but I already know stuff such as higher order differential equations for movement, no need for middle school Khan Academy.
Lionino
2.7kThanks but I already know stuff such as higher order differential equations for movement, no need for middle school Khan Academy.
If the wheel has a circumference of 2 meters, the car will advance 2 meters for each rotation if there is no slippage — Sir2u
Right.
No part of the wheel can advance fast than the car — Sir2u
It can and it does. The wheel makes the car move AND its points on the top half move from a position closer to the back of the car to closer to the front. Therefore it is moving faster than the car.
The linear speed of a point on the circumference of the wheel is given by ω*r where ω is the angular speed and r the radius of the wheel, the linear speed is always equal to the car's speed as long as it does not slip. For a car moving to the right, the horizontal component of the linear speed of that point on the wheel in reference to the ground is ω*r*sinθ where θ is the angle the point makes with the floor and θ=0 being the left corner of the wheel. Due to the oscillation of sinθ, the horizontal component of the speed can be anything from -ω*r to ω*r. Adding those two to the car's speed ω*r, we get 0 or 2*ω*r.
I am not going to be arguing about physics unless you show a system of equations that refutes what I said.
Welcome to The Philosophy Forum!
Get involved in philosophical discussions about knowledge, truth, language, consciousness, science, politics, religion, logic and mathematics, art, history, and lots more. No ads, no clutter, and very little agreement — just fascinating conversations.
Categories
- Guest category
- Phil. Writing Challenge - June 2025
- The Lounge
- General Philosophy
- Metaphysics & Epistemology
- Philosophy of Mind
- Ethics
- Political Philosophy
- Philosophy of Art
- Logic & Philosophy of Mathematics
- Philosophy of Religion
- Philosophy of Science
- Philosophy of Language
- Interesting Stuff
- Politics and Current Affairs
- Humanities and Social Sciences
- Science and Technology
- Non-English Discussion
- German Discussion
- Spanish Discussion
- Learning Centre
- Resources
- Books and Papers
- Reading groups
- Questions
- Guest Speakers
- David Pearce
- Massimo Pigliucci
- Debates
- Debate Proposals
- Debate Discussion
- Feedback
- Article submissions
- About TPF
- Help
More Discussions
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum












