-
 Moliere
6.5kOK I've worked my way through to the last step with that help. I think you're right about the presentation being confusing. When I started thinking of the equality symbol as more like the --> symbol that helped, and then when I started looking at the initials like things I could plug into my starting point in a step-wise fashion then that also helped.
Moliere
6.5kOK I've worked my way through to the last step with that help. I think you're right about the presentation being confusing. When I started thinking of the equality symbol as more like the --> symbol that helped, and then when I started looking at the initials like things I could plug into my starting point in a step-wise fashion then that also helped.
The last step I'm struggling with because it seems like I have to Let p = -- is it allowed to switch what p equals in the middle of a demonstration? -
 unenlightened
10kOk. the rest is easy, use J1 to stick another nothing expression inside c1, to produce the next line.
unenlightened
10kOk. the rest is easy, use J1 to stick another nothing expression inside c1, to produce the next line.
and then use J2 the right way round this time, to take the second and fourth 'a's outside the whole expression using r = a substitution.
and the last step uses p = to eliminate the whole left side, leaving "a". QED. -
 unenlightened
10kI think maybe the main confusion is that for a proof the result is set out at the beginning as the target; you have to take one side and turn it into the other, which in this case was a bit devious. So you already have the answer, but you have to 'show your working', or in this case, understand his working.
unenlightened
10kI think maybe the main confusion is that for a proof the result is set out at the beginning as the target; you have to take one side and turn it into the other, which in this case was a bit devious. So you already have the answer, but you have to 'show your working', or in this case, understand his working. -
 Moliere
6.5kWell, that answers that question. Cool. Then I'm tracking!
Moliere
6.5kWell, that answers that question. Cool. Then I'm tracking!
And actually I had that thought, but then I thought -- well of course we can Let p = whatever we want. It's the form that matters. If I wanted to make sure I was tracking things correctly I could introduce another variable, like s, and let it equal and the form would still work out.
Thanks for working that with me. -
 unenlightened
10kExcellent. Once I had that one, I had little trouble up to C6.
unenlightened
10kExcellent. Once I had that one, I had little trouble up to C6.
C7, 8, & 9, I'm still struggling with. -
 Moliere
6.5kI think I figured out C7 this morning. (and the others prior -- I figured out 5 when it clicked that the unmarked state was taking the place of "b" in using C4)
Moliere
6.5kI think I figured out C7 this morning. (and the others prior -- I figured out 5 when it clicked that the unmarked state was taking the place of "b" in using C4)
By C1 -- , which we apply to the token to obtain
Then by J2:
=
Let p = a, q = and r = c then distribute from the Right-hand side to the left hand side.
Then by C1, Let a = and reflect from the left-hand side to the right hand side to remove the top two crosses to obtain... well, exactly what I just wrote.
End of demonstration for C7. -
 Moliere
6.5kC8
Moliere
6.5kC8
(1)
Call C1:
Let C1's a =
Reflect from the right hand side to the left hand side to place two crosses:
(2)
Call J2: =
Let J2's:
p = b, q = c, and r = r and collect r from the left hand side of J2 to the right hand side of J2:
(3)
Call C7:
=
This one took me several guesses. What helped me was to see that the form of C7 has c on both sides of the two separate crosses on its right hand side, and so C7's c must equal (3)'s since the conclusion has collected into two separate crosses.
Once I saw that then I Let C7's a = , and I transposed (3)'s to the right hand side so that it fit the form of C7 more apparently. Then plugging it in sure enough I got C8:
-
 unenlightened
10kC8 was a stinker. I had to look at Wayfarer's video link for that rearrange, and then suddenly it was easy. So we are on the same page, but I'm going to be off line next week for a while - daughter has just bought a flat and needs a free decorator. C9 will have to wait... a hint from the video - the guy thinks the last C attribution in C9 proof is a typo.
unenlightened
10kC8 was a stinker. I had to look at Wayfarer's video link for that rearrange, and then suddenly it was easy. So we are on the same page, but I'm going to be off line next week for a while - daughter has just bought a flat and needs a free decorator. C9 will have to wait... a hint from the video - the guy thinks the last C attribution in C9 proof is a typo. -
 Moliere
6.5kThanks for the tip -- that would have been a frustrating discovery to make on my own. I'll still check it with C6 first to see, but C9 looked like quite a doozy already.
Moliere
6.5kThanks for the tip -- that would have been a frustrating discovery to make on my own. I'll still check it with C6 first to see, but C9 looked like quite a doozy already.
Sometimes it feels like the demonstrations are purposefully harder than need be -- to get you in the habit of switching out variables for one another. After getting this far the substitution rules made more sense upon reading them -- they were formal statements of what we're doing to check Brown's work that were needed to give meaning to "equality".
And I checked out what comes after C9, and can say that I find it confusing. This is the first appearance of "integration" that I could find by checking the names of each transformation from before, and I don't understand what the part with the series of "is changed to" symbolsarearranged means. "The unmarked state is changed to the unmarked state is changed to the unmarked state is equal to the unmarked state is changed to the unmarked state" is the literal translation of the first example, and I don't know what he's getting at with it.
I'll probably at least work out C9 by the time you get back, but probably wait from there. Have a good week! -
 Moliere
6.5kI said that, but I took a hiatus with the USian labor day weekend, and this morning I got stuck on the first transformation of the demonstration of C9. This afternoon I think I worked out the first step, which I'm going to present here because it took me a second to see it.
Moliere
6.5kI said that, but I took a hiatus with the USian labor day weekend, and this morning I got stuck on the first transformation of the demonstration of C9. This afternoon I think I worked out the first step, which I'm going to present here because it took me a second to see it.
=
Just looking for patterns I noticed how the only transformation occurs on the final two depth=2 crosses, so I simplified to looking at those final two crosses alone:
Which to fit the form of C1, as the text suggests, I set this whole expression = a, and from C1 I add two crosses onto the expression:
Which gets us to something close to J2. From J2 let p = and let q = , then the expression resembles the left hand side of J2. Converting to the right hand side of J2, but substituting back into the original expression we obtain:
Which from C1, but this time going from the left hand side to the right hand side to remove two crosses above both X and Y, and plugging this expression back into its place from the original expression we get the first step:
(C9.1)
EDIT:
About an hour later, some random thoughts I'm having while working through these:
One of the things I'm thinking of is how we're showing, from the rules set out so far, how one expression equals another expression. But even though we're using variables I remain uncertain that we have really marked out the domain of expressions such that these are proofs. And further it seems that we could show some other expression could equal one of the other conclusions, like C1. Or, at least, it's not clear to me that these hold as proofs in the same way that numerical expressions with variables have proofs in them, or that other logical systems have proofs in them, like De Morgan's Laws.
To make a list of what we are able to do so far: substitution, the marked state, the unmarked state, variables, equality, and step-wise transformation from J1/J2 (and all demonstrations from J1/J2). The demonstrations are claiming to be a calculus of the marked or unmarked state, but how to delimit that space such that these demonstrations are proofs, in that they hold for the whole space of all expressions? Are there no other expressions other than the marked/unmarked state, or is there a value in-between marked/unmarked? Or is the law of the excluded middle an assumption of the calculus such that we also can conclude that?
One of the differences I'm seeing between this logic and the other two I listed (algebra, Boolean logic) is the lack of negation. There is no negation in this system. There is marked/unmarked, but no negation of the marked/unmarked, which I wonder if that somehow ties into making a consistent system of symbol manipulation. It makes me think that we can think of the unmarked state as more in analogue with 1/1, like it can perpetuate anywhere within an expression in the same way that (1/1) can always be added to either side of an algebraic expression.
Still meandery. One thing these exercises is providing me is a vantage from which to see how logical systems work in the abstract, or at least a vantage to reach for that perspective. ALSO, back of the mind thought, if negation never shows up then perhaps Godel's Incompleteness Theorem will not apply here. (Back of the mind for so many reasons... but I've noticed that the system may not be powerful enough to represent arithmetic, and that's why I have the thought)
Also interesting to note how the proofs of J1/J2 work by showing all cases: under the assumption that p,q, or r is such and such we show the whole expression is equal in all possible cases. This is important, I think, because it may be the case that at some additional variable point we would be unable to check by the method of all cases (which reminds me of truth-tables' check for validity, actually), and so one wonders if a multitude of variables could lead to undecidable, or multiply decidable expressions such that they could lead to both the marked/unmarked state. I think this is the thing that would have to be secured to count these demonstrations as proofs -- we have the demonstration, but is it possible for the demonstration to turn out the opposite value? Like with C1, is it possible to come up with an expression that reduced a-cross-cross to the unmarked state without a from the transformation rules? It's a niggling thought at the back of my mind, and it would be hard to find such an expression, and I may just be completely off base. But hey, sharing the thoughts in the spirit of the thread. -
 Moliere
6.5k(C9.1)
Moliere
6.5k(C9.1)
Noticing that the form closely matches C8... (Note, I thought I had it in typing it out but then noticed I'm making a mistake, so the first part is a failed attempt at demonstrating this step, but after the break I figured out my mistake and demonstrate the step from C9.1 to C9.2)
Let C8's...
a =
Because that's the only expression which appears under both crosses in C8's transformation to the right-hand-side.
b =
c =
r =
Then plugging these values into the right hand side of C8 we get:
And then we remove the double brackets using C1 and re-arrange the expressions to obtain (though it looks more like 5 times rather than thrice?) (Actually I'm making a mistake here... I'm noticing that there's an added cross in the final conclusion that I'm not accounting for... hrm, hrm, hrm...)
(C9.2) (but not obtained by the above procedure)
**************
Something I like to demonstrate in my postings here is that I'm constantly changing my mind, or noticing mistakes -- my thought is that the finished product never looks like how you get there, and I think that this forum is at its best when sharing our process of thinking in all of its messiness, in all of its faults. So I'm keeping the mistake up above, while working out the correct demonstration here (and simply adding to the post so as not to clog the front page too much) (Also why I'm fine with repeating myself, or going over old ground again)
And I figured out my mistake. The reason I had extra crosses, and needed to perform C1 more than thrice, is that the solution should be--
Let C8's...
a=
b =
c =
r =
Then plugging into the right hand side of C8 we obtain:
And then we can remove the double crosses, three times (C1 thrice), to obtain:
(C9.12)
Which easily re-arranges to:
(C9.2) -
 Moliere
6.5kAnd let's see if I can finish it out now...
Moliere
6.5kAnd let's see if I can finish it out now...
(C9.12) from above shows how C2 can be used to obtain C9.3 more easily.
Let C2's a= unmarked state, and b= r for the right-hand expression in C9.12
= (C2)
Plugging the right hand expression of C9.12 into the right-hand side of C2, while keeping as is...
--> (C9.13)
We remove the double cross with C1 and put back into the original expression to get C9.3:
(C9.3)
Looking at the differences between C9.3 and C9.4 I thought that only the left-hand cross was involved in the transformation, but then saw that we're using C2 and the only way to get r-x-y-cross underneath that cross is by setting C2's b = r-x-y-cross, and a is everything else underneath the left-hand cross. It's a transformation from the right-hand-side of C2 to the left-hand-side.
(C9.4)
This last step took some guesses for me. What worked was using C7. I could see that we really just want to get rid of some of the terms underneath the left-hand cross of C9.4. I pretty much just guess-and-checked my way to a solution.
C7, but inverted to show the direction of transformation:
=
Let C7's a =xy, b =xy, and c = r. Ignoring, from C9.4, and maintaining b and a from C9.4 (but erasing the cross that all of this is contained in to make it less bulky)
--> (C9.5)
Which is close to where we want to get to, we just want to remove the redundant part at depth 3 and 4.
For that I went to C2:
=
Taking just the expression:
Let C2's a = unmarked state
Let C2's b = xy
It becomes
(C9.6)
Then take this expression into C3:
=
Let C3's a = xy and C9.6 reduces to a single cross.
Plug C9.6 reduced back into C9.5:
Using C1 we reduce the double crosses over the unmarked state and plug this back into C9.4 and rearrange we obtain C9's conclusion:
And so we have C9:
= (C9)
Which, yup, I can get the conclusion, but it certainly didn't involve using C6 -- and I tried to do it that way a few times but concluded it couldn't be used because there's just not that form present in the expression of interest. So a bit of a guess-and-check based on what we're trying to obtain got me through the demonstrations.
There's something odd about letting b = xy and a = xy, but I don't really see a reason within the logic presented so far to not allow two different variables to be assigned to similar names at different parts of an expression so I just went with it. But it does seem kind of funny. (Also noting how Theorem 12 states that I should use T10 in place of J2, and I didn't really use J2... I was just looking for a way to make the equation work. So that derivation may be wrong, or at least wasn't what GSB had in mind -- but it seems to follow still)
I have now figured out what he meant by "integration". I missed that C3 was named integration, and so this is him pulling out one of the sub-steps in the demonstration of C3 and calling it "integration".
That leaves the bit where he says "Thus if we consider the equivalence of steps..." which I'm still scratching me head on. I understand that the steps have an order to them, and so reduce depending upon the order of transformations. But his conclusion that "therefore the unmarked state is equivalent to a step" doesn't make sense to me. He demonstrated that taking steps is inconsistent and so he concludes that the unmarked state is a step rather than not putting steps into the calculus -- which is what I'd do since steps had never been introduced as a member of the calculus. We've been working through the marked state, the unmarked state, equivalence, and transformation through substitution. The steps are semi-arbitrary in that we can set any part of an expression equal some other conclusion as long as the forms match up. Why on earth would I take a step as a part of the calculus and set it equal to the unmarked state? -
 Moliere
6.5kI said I'd wait but I'm not :P :D -- I finished the book today. But that chapter on time isn't clicking.
Moliere
6.5kI said I'd wait but I'm not :P :D -- I finished the book today. But that chapter on time isn't clicking.
I'm tempted at this point to just grant chapter 7. I checked T10 through the proof by example of J2 and it works out, but since I didn't get to C9 the same as GSB, and it looks close enough for me, I'm fine with just allowing it and moving on. After working through those examples the text is reading a lot easier and I can kind of see how it's good enough for me. :D -- it was fun to work through the nitty gritty puzzles, but I'm starting to think "OK, I'm ready for a point now"
Seventh Cannon is what made me think the above -- it pretty much lays out what we've been doing in the demonstrations, but allows you to use the algebra now.
The bits on time: we get the conclusion I was thinking of, which is interesting to me!, that there are undecidable expressions (now that we have functions that go to infinity).
One thing I'm thinking is you could just posit another space-dimension to accommodate GSB's "cross in a plane", but I'm ok with saying this is space-time instead.
The oscillator function makes me want to take back what I said earlier about negation. It seems like we're close to negation with it because of the relationship between the two spaces inverts, but it's never named.
But I can say I've officially lost the plot at page 62's "Time in finite expression" -- I don't understand Figure 3, or most of the figures after that. The only one I get right now is page 65's rendition of E1.
But also I kind of continued past when I normally would just because I was hooked. I've officially finished the book now, but without as much math ;). Still chewing on the ending. -
 Moliere
6.5kTyping out the ending, because it's probably the most interesting philosophical part:
Moliere
6.5kTyping out the ending, because it's probably the most interesting philosophical part:
An observer, since he distinguishes the space he occupies, is also a mark.
In the experiments above, imagine the circles to be forms and their circumferences to be the distinctions shaping the spaces of these forms.
In this conception a distinction drawn in any space is a mark distinguishing the space. Equally and conversely, any mark in a space draws a distinction.
We see now that the first distinction, the mark, and the observer are not only interchangeable, but, in the form, identical
While I've admitted ignorance to certain parts of GSB's demonstration, I'm not sure about the conclusion here. Not that it's wrong, only that I'm uncertain that it's earned.
Observers and such haven't really shown up until this point. He's asking us to interpret ourselves as an "m" outside of a circle where the circle is the forms around us. But this would be the simple subject, if it can be reduced to an "m"? Or no? It's not clear, because "observer" shows up at the very end.
All the same I think I like "a distinction drawn in any space is a mark distinguishing the space" -- to mark a space one must mark. Even "the unmarked state" has been used so far as equal to variables, and so works, in a sense, as a marked space would (in a different way from the way space pervades expressions)
But I'd say that GSB sees something I don't, at the end. And I suspect it's because he's an idealist. He can see that the first distinction makes the observer interchangeable with the mark because he believes that, at base, this is all mind-stuff and the forms we see are mentally constructed? Or something along those lines.
But all I see is a mark, and a man who wants to be that mark. -
 Moliere
6.5kWith that being said: I really like the last chapter because it's close to what I was writing out, once upon a time, when attempting to invent a purely spacial logic (that didn't work out, and so I threw it away as nonsense). Also I enjoyed working through a calculus that isn't the same as all the others, though there are parts I'm still uncertain about. And I enjoyed GSB's fusion of poetry with math, which is something I have a soft spot for. (EDIT: Might be a bit of a surprise given my approach so far -- but I wanted to treat the book as a logic in addition to its poetic value, and thought maybe that was the part I could contribute to for understanding the text)
Moliere
6.5kWith that being said: I really like the last chapter because it's close to what I was writing out, once upon a time, when attempting to invent a purely spacial logic (that didn't work out, and so I threw it away as nonsense). Also I enjoyed working through a calculus that isn't the same as all the others, though there are parts I'm still uncertain about. And I enjoyed GSB's fusion of poetry with math, which is something I have a soft spot for. (EDIT: Might be a bit of a surprise given my approach so far -- but I wanted to treat the book as a logic in addition to its poetic value, and thought maybe that was the part I could contribute to for understanding the text)
Good recommendation @unenlightened, and thanks for the prodding and motivation. I would not have finished the book without your help. -
 unenlightened
10kI am back from 'the flat of no internet', where the heat has been drying the paint before I had time to spread it evenly on the wall. And happily @Moliere has done all the hard work for me, so I can waffle a bit on interpretations and applications. But first ...
unenlightened
10kI am back from 'the flat of no internet', where the heat has been drying the paint before I had time to spread it evenly on the wall. And happily @Moliere has done all the hard work for me, so I can waffle a bit on interpretations and applications. But first ...
The bits on time: we get the conclusion I was thinking of, which is interesting to me!, that there are undecidable expressions (now that we have functions that go to infinity).
One thing I'm thinking is you could just posit another space-dimension to accommodate GSB's "cross in a plane", but I'm ok with saying this is space-time instead. — Moliere
GSB tries the extra space dimension himself, with the idea of a tunnel, but it doesn't quite work, because as soon as the boundary is undermined, it becomes 'incontinent'. he still needs time to keep the distinction clear. But if we go back to switches and circuits, everything is understandable. There is a very simple circuit that works as a buzzer or operates an electric bell, and at the heart of it is a switch that operates itself.
This is not the switch one operates to make the buzzer buzz, or the fire alarm ring, but an internal switch, that, as it operates the hammer on the bell, also switches itself off so that the hammer immediately falls back, and switches the circuit on again. The circuit cycles on and off indefinitely. We have electro-mechanical feedback; we have time, because any number of spacial dimensions cannot do the job of the same circuit being on and off - only time as change resolves the contradiction and maintains the continence of the distinction.
But I'll go back a bit, not to all those theorems , that are just extensions of what we already have, but to this:Indicative space
If So is the pervasive space of e, the value of e is its value to So. If e is the whole expression in So, So takes the value of e and
we can call So the indicative space of e.
In evaluating e we imagine ourselves in So with e and thus surrounded by the unwritten cross which is the boundary to S-1. — P.42
A formal system is always imaginary, but normally, one imagines oneself outside the system commanding, evaluating, operating the system from outside, that is from "S-1". But here, that is ruled out, because outside and inside are the form of the first distinction. 'Value' is always relational, and always 'a difference that makes a difference'. To put it another way, there is no absolute value and no absolute outside, one is always in one's world, that one creates in distinguishing. -
 Moliere
6.5kOK So rather than a Cartesian subject: "One is always in one's world" has a phenomenological sound to it. The world is composed of distinctions, in this case, some of which include me (inside) and the rest of which doesn't (outside), but which are still together as one world: the world composed of distinctions. The book is gesturing towards a flow of distinctions upon distinctions with the first distinction holding for all distinctions thereafter.
Moliere
6.5kOK So rather than a Cartesian subject: "One is always in one's world" has a phenomenological sound to it. The world is composed of distinctions, in this case, some of which include me (inside) and the rest of which doesn't (outside), but which are still together as one world: the world composed of distinctions. The book is gesturing towards a flow of distinctions upon distinctions with the first distinction holding for all distinctions thereafter. -
 unenlightened
10kLet us then consider, for a moment, the world as described by the physicist. It consists of a number of fundamental particles which, if shot through their own space, appear as waves, and are thus (as in Chapter 11), of the same laminated structure as pearls or onions, and other wave forms called electromagnetic which it is convenient, by Occam's razor, to consider as travelling through space with a standard velocity. All these appear bound by certain natural laws which indicate the form of their relationship.
unenlightened
10kLet us then consider, for a moment, the world as described by the physicist. It consists of a number of fundamental particles which, if shot through their own space, appear as waves, and are thus (as in Chapter 11), of the same laminated structure as pearls or onions, and other wave forms called electromagnetic which it is convenient, by Occam's razor, to consider as travelling through space with a standard velocity. All these appear bound by certain natural laws which indicate the form of their relationship.
Now the physicist himself, who describes all this, is, in his own account, himself constructed of it. He is, in short, made of a conglomeration of the very particulars he describes, no more, no less, bound together by and obeying such general laws as he himself has managed to find and to record.
Thus we cannot escape the fact that the world we know is constructed in order (and thus in such a way as to be able) to see itself.
This is indeed amazing.
Not so much in view of what it sees, although this may appear fantastic enough, but in respect of the fact that it can see at all. But in order to do so, evidently it must first cut itself up into at least one state which sees, and at least one other state which is seen. In this severed and mutilated condition, whatever it sees is only partially itself. We may take it that the world undoubtedly is itself (i.e. is indistinct from itself), but, in any attempt to see itself as an object, it must, equally undoubtedly, act* so as to make itself distinct from, and therefore false to, itself. In this condition it will always partially elude itself. — CHAPTER 12
The world is composed of distinctions... — Moliere
Yeah but, no but...
I have a problem with putting it like this, because it seems to be making a distinction between what the world is composed of, and What it might have been composed of, or might have been thought to be composed of... But that cannot be. One could at least equally say that the world is decomposed of distinctions. "In the beginning was the Word."
There is a sense in which there cannot be a world unseen, and a sense in which there obviously can and must be before seeing can arise. There must be physics before there can be physicists, but physicists are nothing other than that physics. But the first distinction is made by the first cell, and then the first re-entry of the first distinction into itself by the first language speakers, and then...
The Observer is the observed. — Krishnamurti
Wake up to find out that you are the eyes of the world. — The Grateful Dead
I would not say that the world is composed of eyes, but it has eyes, and we are those eyes.
————————————————————————
There's one last bit that I would still like to get a more firm handle on, which is the second half of Ch.11, on memory, counting and imaginary values. The book is incredibly compressed at this stage, and a whole new notation introduced if not more than one. I have a half understanding of it, and my next post will attempt to convey as much as I can of that half. -
 Count Timothy von Icarus
4.3kI found this summary fairly interesting: https://www.projectenportfolio.nl/images/1/16/Robertson-Laws_of_Form.pdf
Count Timothy von Icarus
4.3kI found this summary fairly interesting: https://www.projectenportfolio.nl/images/1/16/Robertson-Laws_of_Form.pdf
Axioms are considered primitive assumptions beyond questions of true or falsity. The remainder of a system is then developed formally from these primitives. In contrast, Spencer-Brown’s axioms seem to be indisputable conclusions about the deepest archetypal nature of reality. They formally express the little we can say about something and nothing...
Once bitten, twice shy—mathematicians became much more concerned with abstraction and formality. They separated what they knew in their mathematical world from what scientists asserted about the physical world. Mathematics was supposed to be the science which dealt with the formal rules for manipulating meaningless signs. Spencer-Brown’s attempt to develop
Interesting vis-a-vis the original thread that sparked this one. Is there a "logic-like reality that exists outside the minds of individuals," etc.
Sometimes I wonder if the discoveries of the early-20th century should have been taken as a warning against strict bivalance and "truth as objectivity," rather than as an argument for deflating truth (as they generally were).
I.e.:
Meanwhile, if the fear of falling into error introduces an element of distrust into science, which without any scruples of that sort goes to work and actually does know, it is not easy to understand why, conversely, a distrust should not be placed in this very distrust, and why we should not take care lest the fear of error is not just the initial error. As a matter of fact, this fear presupposes something, indeed a great deal, as truth, and supports its scruples and consequences on what should itself be examined beforehand to see whether it is truth. It starts with ideas of knowledge as an instrument, and as a medium; and presupposes a distinction of ourselves from this knowledge. More especially it takes for granted that the Absolute stands on one side, and that knowledge on the other side, by itself and cut off from the Absolute, is still something real; in other words, that knowledge, which, by being outside the Absolute, is certainly also outside truth, is nevertheless true — a position which, while calling itself fear of error, makes itself known rather as fear of the truth.
G.W.F. Hegel, the Phenomenology Sec 74
The idea of imaginary numbers as oscillations is interesting too. I have always seen them described as a number line running orthogonal to the real number line instead. Imaginary numbers are interesting in general because they seem to be a move to admit some sort of paraconsistency into mathematics for pragmatic expedience. I assume they have since been grounded in mathematical logic somehow? I just recall from mathematical histories that they were initially accepted on the grounds that "it works, don't it?" as with zero as well.
Interesting quote from Varela, who expanded Brown's system to include self-reference as a third mark, a move made to make it more usable with biology, where self-reference is central.
When [Norbert] Wiener brought the feedback idea to the foreground, not only did it become immediately recognized as a fundamental concept, but it also raised major philosophical questions as to the validity of the cause-effect doctrine.…the nature of feedback is that it gives a mechanism, which is independent of particular properties, of components, for constituting a stable unit. And from this mechanism, the appearance of stability gives a rationale to the observed purposive behavior of systems and a possibility of understanding teleology.…Since Wiener, the analysis of various types of systems has borne this same generalization: Whenever a whole is identified, its interactions turn out to be circularly interconnected, and cannot be taken as linear cause-effect relationships if one is not to lose the system’s characteristics (
Reading Terrance Deacon's Incomplete Nature right now, it's clear this thread has been developed a great deal, but not resolved. Deacon tries to explain how purposefulness emerges by reintroducing Aristotle's formal cause via-thermodynamics and an explicitly process-based, as opposed to substance metaphysics.
All very interesting, but damn hard to wrap one's mind around. I do wonder why it is that it has taken so long for the process view to take over. Is it necessarily less intuitive, or is the problem that we drill a sort of naive corpuscularism, a substance metaphysics, into kids for the first 14-18 years of their education? It certainly seems less intuitive. I sort of buy into Donald Hoffman's argument that we evolved to want to focus on concrete objects (thus excluding the "nothing").
Side note: It's interesting that Brown was working on network issues. I've seen some articles on information theoretic/categorical models of quantum mechanics that attempt to explain physics as a network. This in turn, allows us to recreate standard QM in a different language, but also explains entanglement in a more intuitive network-based model (or so the author claimed, I did not find anything intuitive about the paper lol). I do find the idea of modeling reality as networks or possibility trees interesting though. But again, it's easier to conceptualize the network as a fundamental thing, rather then that the network simply is a model of process and relation, which seems to be the true basic entity! -
 wonderer1
2.4kI do wonder why it is that it has taken so long for the process view to take over. Is it necessarily less intuitive, or is the problem that we drill a sort of naive corpuscularism, a substance metaphysics, into kids for the first 14-18 years of their education? It certainly seems less intuitive. I sort of buy into Donald Hoffman's argument that we evolved to want to focus on concrete objects (thus excluding the "nothing"). — Count Timothy von Icarus
wonderer1
2.4kI do wonder why it is that it has taken so long for the process view to take over. Is it necessarily less intuitive, or is the problem that we drill a sort of naive corpuscularism, a substance metaphysics, into kids for the first 14-18 years of their education? It certainly seems less intuitive. I sort of buy into Donald Hoffman's argument that we evolved to want to focus on concrete objects (thus excluding the "nothing"). — Count Timothy von Icarus
Off the top of my head I can't think of many easily observable examples of feedback outside of social interactions, so I think it is pretty natural that people don't tend to have intuitions that are informed by observing feedback systems. (I suppose the notion of karma suggests somewhat the idea of a feedback sysyem.) I don't see it as so much a matter of our educational systems, as a matter of our lacking the perceptual and cognitive systems to see the feedback occurring in things around us.
I look into some types of feedback systems routinely, and have intuitions conducive to understanding feedback systems to a greater degree than most, but it takes expensive instrumentation for me to be able to observe the relevant processes. I'd have to think about how better intuitions about feedback systems could be cost effectively instilled during K-12 education. -
 Count Timothy von Icarus
4.3k
Count Timothy von Icarus
4.3k
I didn't mean feedback necessarily, just the view that process might be seen as fundemental, not substance. That what a thing is might not be best defined by "what it is made of." For example, heat is a measure of average motion, not a thing. Fire is a chemical reaction, not its own substance. So these are best understood as processes not things, but I was always given the view that at any deeper level substances must define reality.
But I suppose the basics of feedback loops are important too. I do feel like I was exposed to that early on. For example, we sweat because we're hot, we get cool from evaporation, and then we stop being hot - negative feedback, or positive feedback too. -
 Moliere
6.5kBut the first distinction is made by the first cell, and then the first re-entry of the first distinction into itself by the first language speakers, and then...
Moliere
6.5kBut the first distinction is made by the first cell, and then the first re-entry of the first distinction into itself by the first language speakers, and then...
The Observer is the observed.
— Krishnamurti
Wake up to find out that you are the eyes of the world.
— The Grateful Dead
I would not say that the world is composed of eyes, but it has eyes, and we are those eyes. — unenlightened
There's a flag I want to put on "first cell", but it feels too off topic.
Granting the first cell making a distinction, which I can agree with, it's interesting how the story can be used for a single developing organism -- a story from birth until here we are talking -- as well as the development of organisms. "then the first re-entry of the first distinction into itself by the first language speakers" helped click some of GSB to his wider, philosophical sense that I haven't been grasping (and, truthfully, I'm still feeling around about).
"The world has eyes" is a nice phrase. It feels mystical in that way that tries to make a reflective statement -- where we talk of the world, which is usually not ourselves, but then it fits us within the world as we see our own eyes in our minds-eye -- that is, through language (or at least with a great deal of assistance from language)
When you finish with your next post: What do you make of 's linked summary? -
 Moliere
6.5kI found this summary fairly interesting: https://www.projectenportfolio.nl/images/1/16/Robertson-Laws_of_Form.pdf — Count Timothy von Icarus
Moliere
6.5kI found this summary fairly interesting: https://www.projectenportfolio.nl/images/1/16/Robertson-Laws_of_Form.pdf — Count Timothy von Icarus
That helped me -- it's nice to have an interpretation that's been worked through by someone else. I didn't realize that GSB's algebra is formally equivalent to Boolean logic (although now that I'm saying that I'm beginning to ask myself, just what *is* formal equivalency? I've sort of just taken that assertion at face value from people more knowledgeable than I). Also I didn't pick up the similarity between self-reference and re-entry.
Side note: It's interesting that Brown was working on network issues. I've seen some articles on information theoretic/categorical models of quantum mechanics that attempt to explain physics as a network. This in turn, allows us to recreate standard QM in a different language, but also explains entanglement in a more intuitive network-based model (or so the author claimed, I did not find anything intuitive about the paper lol). I do find the idea of modeling reality as networks or possibility trees interesting though. But again, it's easier to conceptualize the network as a fundamental thing, rather then that the network simply is a model of process and relation, which seems to be the true basic entity! — Count Timothy von Icarus
Yup, I find that part of what's fascinating in the book. Since the logic was developed in tandem with a practice I'm interested to know it from that practical angle more. -
 unenlightened
10kToday is Wednesday.
unenlightened
10kToday is Wednesday.
The above statement is true as I write, but may well be false as you read. Logic would prefer to be timeless and eternal, and has difficulty dealing with the unpleasantness of times changing.
Six days shalt thou labour and be false, but on the seventh day, thou shalt again be true.
Here's another related piece, fairly short and understandable.
http://homepages.math.uic.edu/~kauffman/TimeParadox.pdf -
 Moliere
6.5k
Moliere
6.5k
I agree that classical logic doesn't deal with time very well. That's part of what allowed Kant to distinguish between Logic As Such, and Transcendental Logic. As well as providing a conceptual entry into Hegel's philosophy.
To evaluate the difficulty of logic, on the whole, dealing with time I'd have to do more homework on logic. Just looking over this: https://plato.stanford.edu/entries/logic-temporal/ -- but it could be that GSB's logic would fit in here, and so "difficulty" is what's being dealt with in Laws of Form. In that case there'd be choices to make on which logic, and I'm not sure how I'd make a choice. (More homework necessary on my part, basically) ((EDIT: Though I should note that it's necessary on my part specifically because of what I'm interested in. I don't think because I'm wanting to bridge these things that means much about GSB's book -- it's more a me thing))
Here's another related piece, fairly short and understandable.
http://homepages.math.uic.edu/~kauffman/TimeParadox.pdf — unenlightened
Another good read. It hits a lot of points of interest for me -- the liar's paradox is one of those I keep going back to, and I found the dual-functions which iterate back and forth in a time series really interesting, and it's interesting how Kauffman links all of these things back to GSB. -
 Moliere
6.5kI'm looking at Chapter 11 again this morning, and having taken a break for the nitty-gritty I wanted to see if I could understand the derivation of infinitely iterating functions to get a better grip on time and oscillations in the book. I'm having trouble, on page 81, of understanding the third step where J2 is called.
Moliere
6.5kI'm looking at Chapter 11 again this morning, and having taken a break for the nitty-gritty I wanted to see if I could understand the derivation of infinitely iterating functions to get a better grip on time and oscillations in the book. I'm having trouble, on page 81, of understanding the third step where J2 is called.
Anyone else work out this demonstration yet? -
 unenlightened
10kI'm having trouble, on page 81, of understanding the third step where J2 is called. — Moliere
unenlightened
10kI'm having trouble, on page 81, of understanding the third step where J2 is called. — Moliere
Are you looking at the 9th canon where he constructs an ever deepening series of nested a's and b's? Page 55 in my version?
If so, you just take the whole right hand expression of a & b as = r. and use J2 in reverse.
This is where I am:
In effect, when a, b both indicate the unmarked state, it remembers which of
them last indicated the marked state. If a, then f= m. If b, then f=n. — p61.
This refers back to the recursive expression derived from the expansion on Page 55 :–
E2.
And also refers back to page 56 right at the bottom:–
m or n
This is extraordinary! A circuit made entirely of switches that has a memory! -
 wonderer1
2.4kThis is extraordinary! A circuit made entirely of switches that has a memory! — unenlightened
wonderer1
2.4kThis is extraordinary! A circuit made entirely of switches that has a memory! — unenlightened
Wow, if someone implemented something like that we could have computers and an internet!
Sorry, couldn't resist. -
 unenlightened
10kWow, if someone implemented something like that we could have computers and an internet! — wonderer1
unenlightened
10kWow, if someone implemented something like that we could have computers and an internet! — wonderer1
Yeah, tempting but stupid. Computer memory is not made of switches. But kudos for bothering to read the thread at all. -
 wonderer1
2.4kYeah, tempting but stupid. Computer memory is not made of switches. But kudos for bothering to read the thread at all. — unenlightened
wonderer1
2.4kYeah, tempting but stupid. Computer memory is not made of switches. But kudos for bothering to read the thread at all. — unenlightened
Well computer memory is implemented in a variety of ways these days, but any modern computer is going to have some memory elements implemented as flip-flops. A simple schematic of a flip-flop is illustrated below.
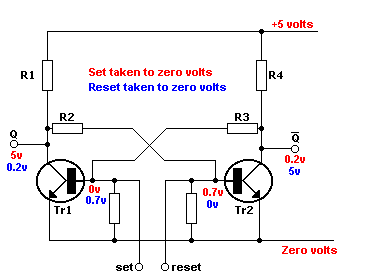
Note that the symbols labeled TR1 and TR2 represent transistors, which for practical purposes are switches.
Older (pre-solid-state) computers used electromagnetically controlled switches with contacts that opened and closed. (relays) This allowed a literal bug to crash a computer. Solid-state switches (transistors) are a big improvement.
Welcome to The Philosophy Forum!
Get involved in philosophical discussions about knowledge, truth, language, consciousness, science, politics, religion, logic and mathematics, art, history, and lots more. No ads, no clutter, and very little agreement — just fascinating conversations.
Categories
- Guest category
- Phil. Writing Challenge - June 2025
- The Lounge
- General Philosophy
- Metaphysics & Epistemology
- Philosophy of Mind
- Ethics
- Political Philosophy
- Philosophy of Art
- Logic & Philosophy of Mathematics
- Philosophy of Religion
- Philosophy of Science
- Philosophy of Language
- Interesting Stuff
- Politics and Current Affairs
- Humanities and Social Sciences
- Science and Technology
- Non-English Discussion
- German Discussion
- Spanish Discussion
- Learning Centre
- Resources
- Books and Papers
- Reading groups
- Questions
- Guest Speakers
- David Pearce
- Massimo Pigliucci
- Debates
- Debate Proposals
- Debate Discussion
- Feedback
- Article submissions
- About TPF
- Help
More Discussions
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum



