-
 Kenosha Kid
3.2kThe electron double-slit experiment, aka Young's slits (not to be confused with my new website), is a treasure-trove of nature. Some have said all of quantum mechanics can be considered from it.
Kenosha Kid
3.2kThe electron double-slit experiment, aka Young's slits (not to be confused with my new website), is a treasure-trove of nature. Some have said all of quantum mechanics can be considered from it.
A brief reminder: when a cathode fires electrons at a screen with two slits, beyond which is another screen, the pattern that builds up on the back screen is bands of light and dark, the dark bands being where few or no electrons strike, the light bands being where more strike. From this we deduce that the electron beam coming from the cathode is a wave.
If the voltage of the cathode is reduced such that only one electron fires out, say, per ten seconds, eventually the same pattern builds up. From this we deduce that each electron is a wave.

In non-relativistic quantum mechanics, this wave is described a the wave equation of the form:
where u is the wavefunction, and all the other terms are operators: E is total energy (the Hamiltonian), A is magnetic potential, p is momentum, V is electric potential, m is mass, and our choice of units is such that all the decorative physical constants like h, c, e, etc. are 1. This is the quantum form of Newtonian mechanics extended to include electromagnetism.
This does not put time and space on equal footing. The solution requires knowledge of u at one time and two places. These are generally derived from physical considerations, e.g. where the electron wavefunction must vanish: two positions where the wavefunction is zero at one time: generally the start.
When u(r,t) is time-evolved according to the above, it spreads out from the cathode, goes through the slits, spreads out from the slits and interferes with itself. Consequently, the wavefunction is defined over many positions at the back screen. And yet when we measure, we see that the electron hit a precise point on the screen.
How the electron got from a field to a point is called the measurement problem, and different solutions to the measurement problem have yielded different interpretations of quantum mechanics. The oldest successful interpretation was the Copenhagen interpretation which states that, upon measurement, the electron wavefunction collapses probabilistically to a single position, the probability given by the absolute square of the wavefunction (the Born rule).
This idea of the absolute square is important. It is how we get from the non-physical wavefunction to a real thing, even as abstract as probability. Why is the wavefunction non-physical? Because it has real and imaginary components: u = Re{u} + i*Im{u}, and nothing observed in nature has this feature. The absolute square of the wavefunction is real, and is obtained by multiplying the wavefunction by its complex conjugate u* = Re{u} - i*Im{u} (note the minus sign). Remembering that i*i = -1, you can see for yourself this is real. We'll come back to this.
There are other probabilistic interpretations, and also some deterministic ones, such as Bohmian mechanics, wherein the electron always has a single-valued position and momentum (hidden variables), and Many-worlds interpretation in which the wavefunction does not collapse but, thanks to the mathematical rules of entanglement, you can never have a term in the wavefunction in which the electron hit the screen at position but you observed it at position .
I'd like to question here the physics of the Copenhagen interpretation -- a reference point for many non-determinists and God-botherers -- because it is incredibly simplistic and I have always thought so. The back screen is treated in an ideal way, which is something physicists often have to do to make problems tractable, but the artefacts of this idealisation are then taken as containing actual insight.
The back screen is a macroscopic object that cannot be treated precisely with quantum mechanics. However, we can still use QM to investigate the issue further. For instance: is the electron wavefunction the only quantity that affects where the electron can be found? Clearly it isn't. An electron cannot, for instance, occupy any part of the screen where an electron already is, unless that second electron can somehow vacate its position (Pauli exclusion principle). This will not reduce the potential sites the electron can occupy to 1, but it will, at any given time, for any given electron, stop the number of sites being a continuum. In the language of condensed matter physics (for the screen is condensed matter), an electron can only go where an electron hole exists. An electron hole in this context is any space where an electron could occupy but does not.
The back screen is a high-entropy object compared with the electron. That is, at any time, it may occupy one of hundreds of thousands or millions of microstates: particular configurations that are energetically equivalent to one another. At one instant t', a position on the screen r' may not admit an electron because it already has one there. At a subsequent instance t'', it might admit an electron at r'. The screen will explore these microstates in a thermodynamic way. i,e, in the same way that a box of gas will have different but energetically equivalent configurations of gas molecules one instant to the next.
[EDIT: To incorporate spin, just extend the concept of the coordinate r.]
So we've reduced the continuum of the screen down to some finite number of available electron holes at time t'. But the electron is again a physical thing: it has energy and momentum. It can't just stop when it fills a hole. It goes on to do other things and, again, this is not considered in the simplified version that sustains the Copenhagen interpretation. Because what it does next is also constrained by the precise microstate of the screen. If it scatters another electron such that it goes from state k --> k'', there has to be an existing hole with state k''. Further, whatever state the scattered electron ends up in, there has to be a hole for that too.
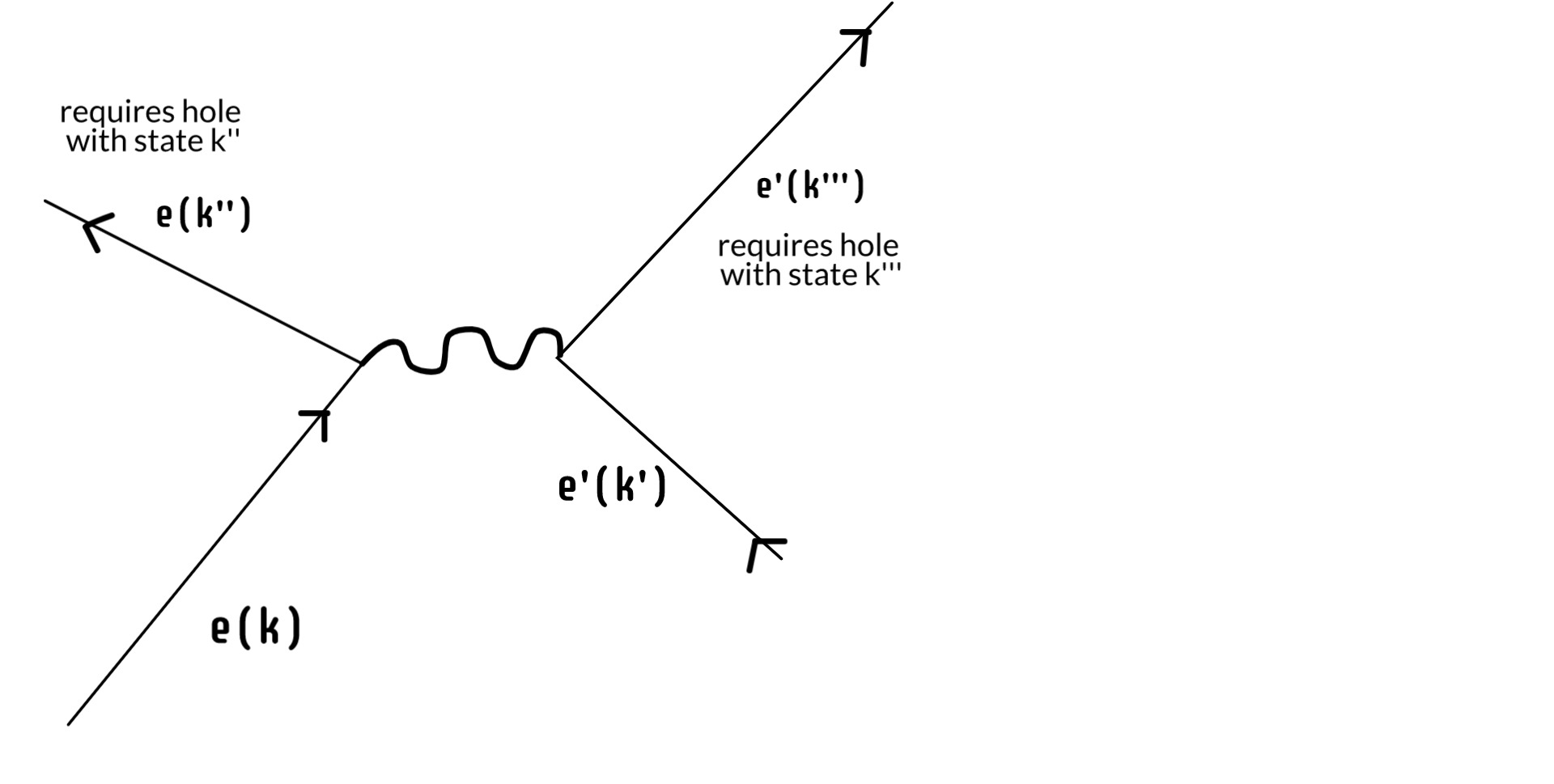
In this way we can reduce that finite number of acceptable positions on the screen ever more by continuing the process. Once it has scattered that first electron, it will scatter another and another, each scattering ever constrained by available states in the screen. We can go further. Eventually the electron, either alone or in an atom, will leave the screen entirely, go off on fun adventures in space and time, until eventually one day it finds a positron -- another kind of electron hole -- where it dies like the swine it always was.
Because the electron's birth and death are the true boundary conditions of its wavefunction! And here we turn to relativity. The relativistic wavefunction is of the form . This puts time and space on equal footing (both energy and momentum are squared), requiring knowledge of the particle at two times, not just one. This is why in relativistic quantum theories, we do not proceed by specifying an initial state, time-evolving it forward, and asking the probability of spontaneously collapsing to a particular final state. Rather, we have to specify the initial and final states first, then ask what the probability is. This is constructed as a Green's function G(r, t; r', t'). You can see that we can swap the primed and unprimed coordinates around. If, for a given G(r, t; r', t') there exists a G(r', t'; r, t), the process X=(r,t) --> X'=(r',t') is reversible. (If the the magnitudes of the two are always equal, the system is in equilibrium.)
We are quite familiar in QM with specifying spatial boundary conditions. For instance, consider a tiny oven, a blackbody radiator. What photons can be emitted inside? We all know that only photons with wavelengths that are integer divisors of 2L, where L is the side of the box, can be sustained (B, C & D below). This is quantisation in a nutshell, and it pops out as solutions of the wave equation with the proper number of spatial boundary conditions.
But let's turn the question around. An atom in the oven emits a photon and later another atom absorbs it and re-emits it (more like A below). How does the first atom know to emit a photon such that an even number of its wavelengths will fit in the box? How does either the atom or the photon know how big the box is? Photon emission is just the de-excitation of an atom from one energy level to a lesser one, and the energy of the oven is given by its temperature, which could be anything.
The question becomes less mysterious when we treat time and space equally: the emitted photon doesn't just have a spatial endpoint, but a temporal one, i.e. the photon can only be emitted when it "knows" where and when it will be absorbed. But how could this be?
Photon emission/absorption is another example of a reversible process. Imagine atom 1, in an excited state, "spontaneously" de-excites, deterministically emitting a photon which then "spontaneously" collapses so as to be absorbed by atom 2 which deterministically excites. Run that movie backwards and you have exactly the same thing, only the thing that's spontaneous is now deterministic and vice versa. The Copenhagen description, though, is irreversible: wavefunction collapse is a loss of information that is not retrieved by simulating the reverse process.

The wave equation for the photon is just E = p. If we start with an initial wavefunction u = d(r), where r is its starting point, the wavefunction will expand and expand. To imagine the time-reversed proces, we begin with its final state. But if we just evolve the final state, that won't get us back to where we started. What can we evolve that will take us from time t' back to time t? To answer this, it's easiest to consider plane waves:
What we want is the same thing but travelling in the opposite direction in space (p --> -p) and time (t --> -t):
This is just the complex conjugate of u, u*, the thing that, when we multiply it by u, gives us the most fundamental real thing QM has: the probability of finding the particle at position r at time t.
Is it a coincidence that the thing that makes a wavefunction real is also the thing that describes that wavefunction in reverse? Not according to the transactional interpretation of quantum mechanics, which holds that the actual trajectories a particle takes are not just determined by the retarded wavefunction going from time t to t', but also the advanced wavefunction going from time t' to t. (Advanced wavefunctions come up in standard QED as well, to yield the electron self-energy). In this interpretation, the complex conjugate is essentially a message from the future. The electron takes the real trajectories it does in part because it has information about where it's going or, from another viewpoint, where it's conjugate came from.
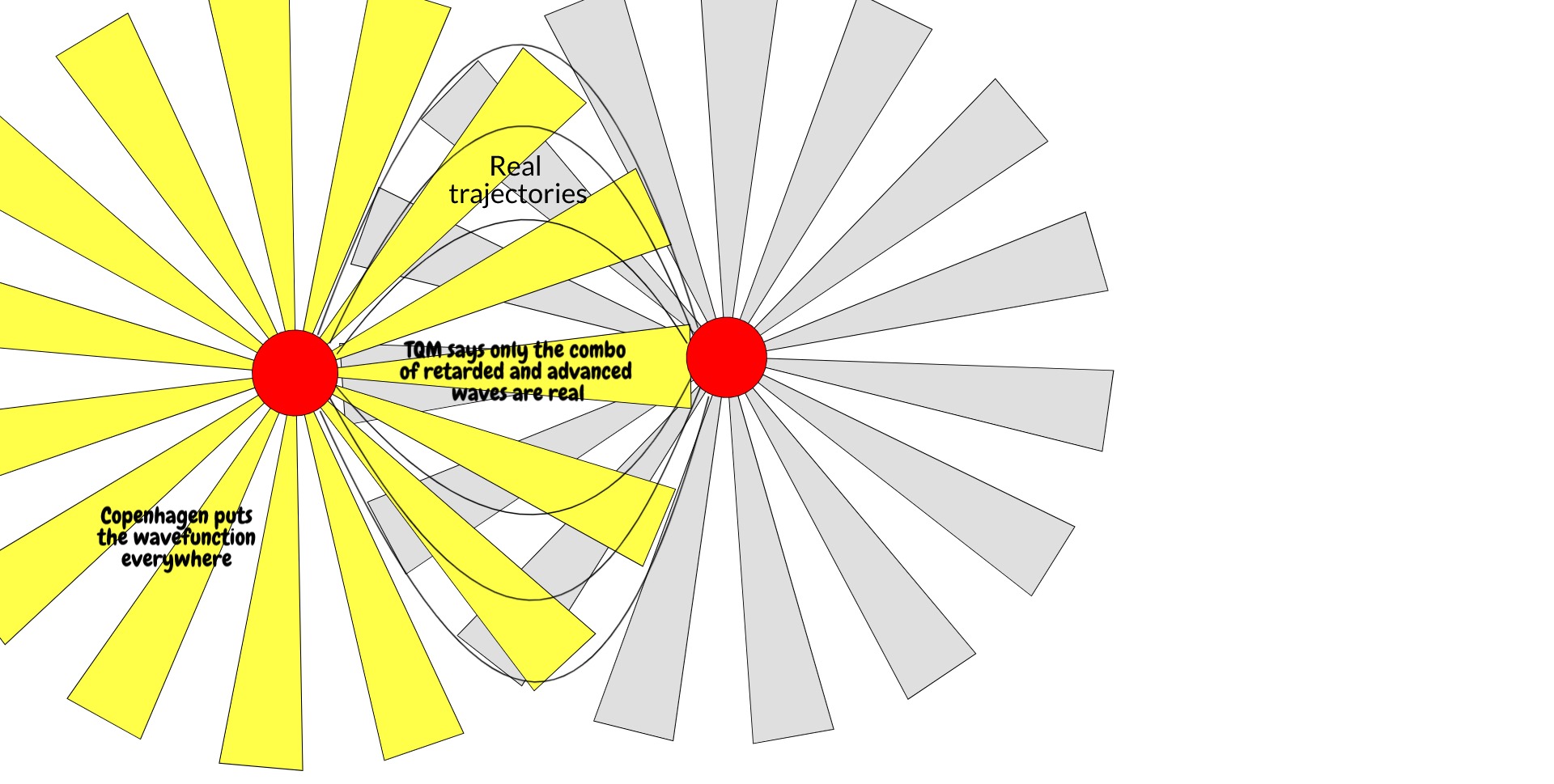
Both the retarded wavefunction going from t -> t' and the advanced wave coming from t' -> t may explore whatever places they want, but only in the trajectories where one is the conjugate of the other do their trajectories become real.
This is inconsistent with Copenhagen, but quite consistent with relativity. It treats space and time equally, requiring two temporal boundary conditions for the electron. Furthermore, it incorporates more physics. We can identify the complex conjugate of the wavefunction as the backwards-in-time emission of an electron hole in the back screen, which incorporates information about the microstate of the screen itself: for an electron hole to be advanced from (r', t'), the microstate of the screen must be such that there exists an electron hole at (r', t'). We would make such a demand of the cathode: for an electron to be emitted at point (r,t) there must be an electron at (r,t). It is only sensible that we do so for the hole the electron will occupy. (It's worth convincing yourself that this hole also has a history. For every electron that vacates position r to occupy position r', it leaves behind a hole and goes to where the hole previously was, describing an electron hole that vacates position r' to occupy position r. We do not need to consider it the same hole throughout, but there must be some conservation of hole-ness.) It conserves indirectly measurable quantum phenomena such as the interference effects in the double-slit experiment because the electron and its hole still go from r to r' or vice versa by every possible trajectory. And yet it eliminates the mysterious collapse mechanism which takes the wavefunction from a field to a singularity.
In a nutshell, my thesis is this... The true boundary conditions of any particle are its birth and death: where and when it was created, and where and when it will be destroyed. These are facts of each particle. This is the full time-dependent wavefunction of the electron which is, relativistically speaking, equivalent to a static 4D wave. Unlike in the QM of the Copenhagen interpretation, the conjugate solution (from death to birth) is also a solution when these boundary conditions are applied. This solution eliminates almost all of the trajectories possible (and expected) in Copenhagen QM. And this is just the single-particle picture.
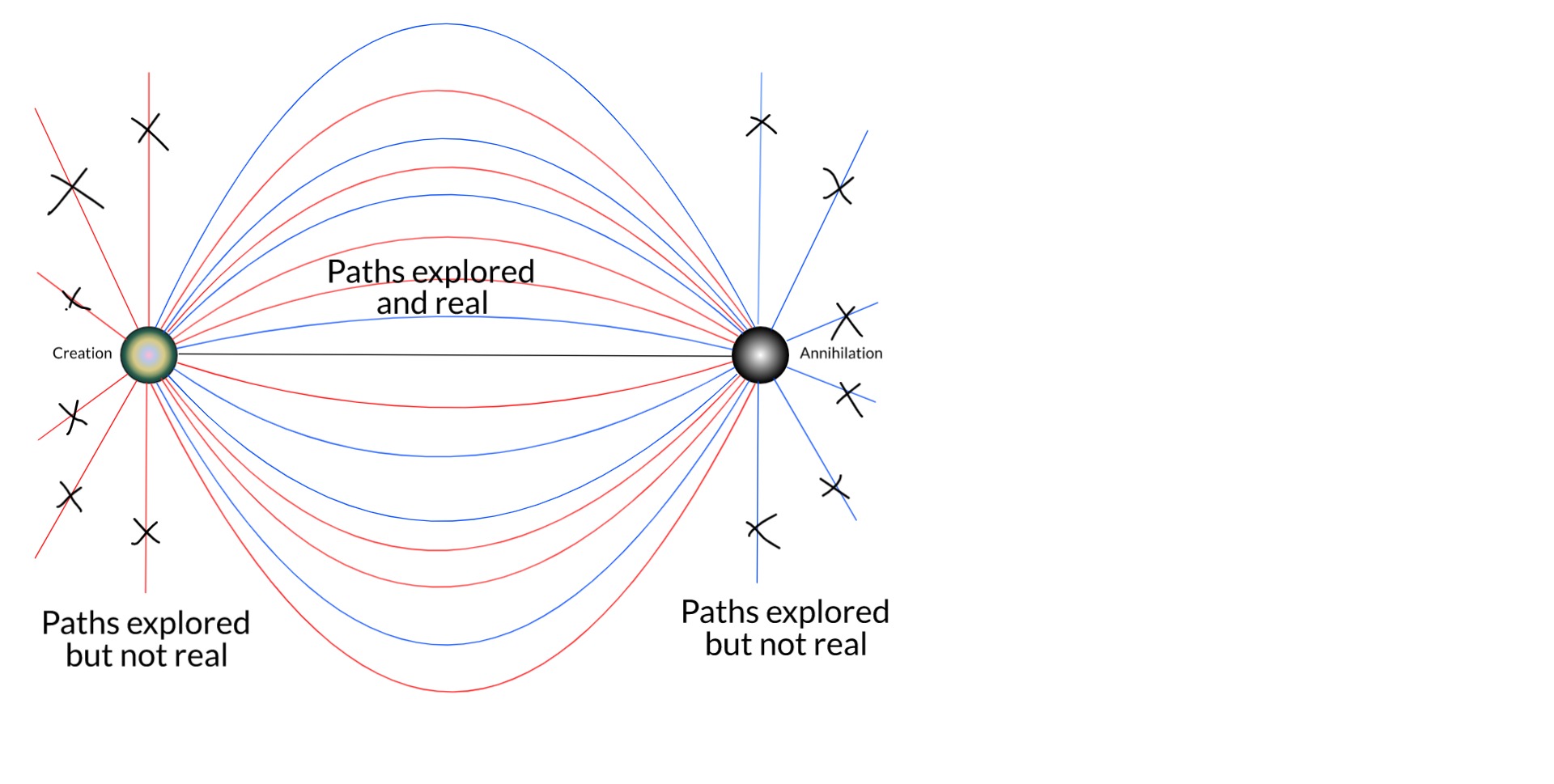
As we expand the picture to include more bodies in the universe, especially the rest of the electronic field, more and more remaining trajectories are removed by things like scattering and Pauli's exclusion principle.
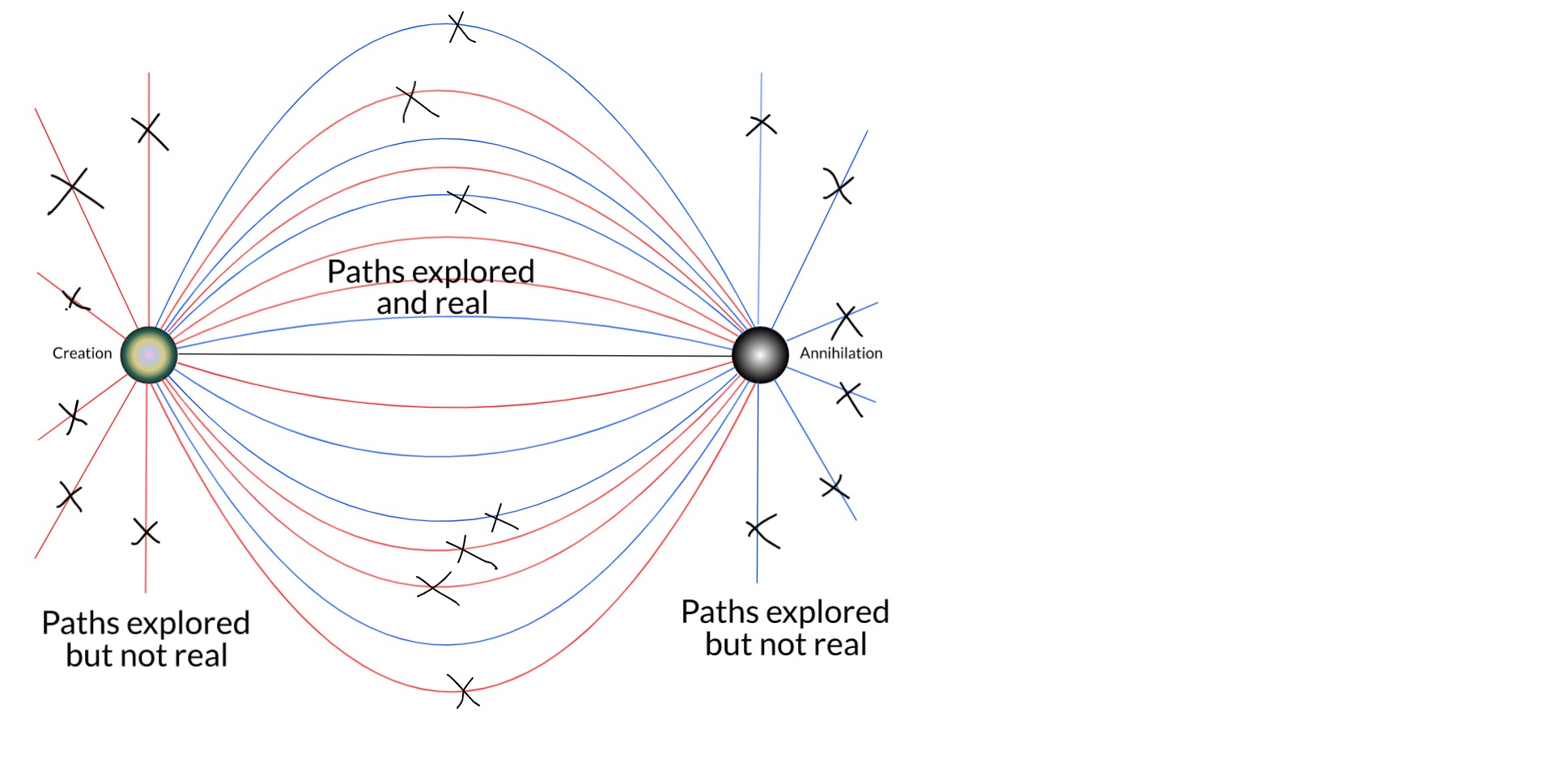
[EDIT: One can also see that single-particle trajectories that otherwise wouldn't be real could be made so by scattering. But Feynman showed that it is the closest paths to straight lines that contribute the most to the sum over histories.]
There is no guarantee here that this will eventually reduce the number of intersections with the screen to 1. But we are a long way from the original Copenhagen picture of an electron that might be found anywhere. I expect that, if we could solve the many-body Dirac equation for the universe (well, it would have to be some cosmologically-consistent generalisation of it), it probably would resolve to 1 intersection.
If not, we're left with a solution that looks like a hugely constrained version of the many-worlds interpretation. I name this the not-many-worlds interpretation of quantum mechanics. -
 Metaphysician Undercover
14.7kHi Kenosha Kid,
Metaphysician Undercover
14.7kHi Kenosha Kid,
I appreciate the well thought out, explicit and thorough description of your thesis. I will reread this a couple times and perhaps make a comment if I see something questionable. -
 Metaphysician Undercover
14.7kI believe that most of the problems which you point to here, are a product of the means of conceptualization. I will try not to be offensive or insulting, because we are all only human after all, but I can say that the concepts employed here are deficient, showing a lack of understanding of the concepts. This leads to odd problems much like the conceptualizations employed by Zeno led to Zeno's paradoxes. We can see with Zeno's paradoxes, that the problem is the result of the means of description, the conceptualizations employed, and how they are employed. Things are described in a way which produces the appearance of paradox. Such is the case in your description above.
Metaphysician Undercover
14.7kI believe that most of the problems which you point to here, are a product of the means of conceptualization. I will try not to be offensive or insulting, because we are all only human after all, but I can say that the concepts employed here are deficient, showing a lack of understanding of the concepts. This leads to odd problems much like the conceptualizations employed by Zeno led to Zeno's paradoxes. We can see with Zeno's paradoxes, that the problem is the result of the means of description, the conceptualizations employed, and how they are employed. Things are described in a way which produces the appearance of paradox. Such is the case in your description above.
So let me start with this idea that the electron (or whatever proposed particle) takes a path, a "trajectory". It is actually impossible that the particle takes a path, and this fact is imposed by the concept of "energy". Energy, in its conceptual formulation is a wave feature. A person might think that a massive object, or a particle, moves from A to B, and brings with it "energy" which is transferred to another object at point B. But the energy according to conventional principles is understood as being transferred from one body to another through wave principles. A moving body has velocity, mass, and momentum according to Newtonian principles, but it does not have "energy". Energy is a feature of the body's relation to something else, and according to conventional principles (Einsteinian), the "something else" is light, or electro-magnetism. Since electro-magnetism is understood and represented by wave principles, the concept of "energy" dictates that energy transmission from one place to another is in the form of a wave. Therefore it makes no sense at all, to say that energy moves from A to B as a particle, because the very concept of "energy" dictates that energy can only be transmitted as a wave. The further discussion as to which trajectory the particle takes therefore, is completely moot, having no significance whatsoever, because whatever it is which transmits from A to B is conceptualized as energy, and energy transmits as a wave, not a particle. There is no particle which moves from A to B, only energy, and by conventional principles energy is transmitted as a wave. The possibility of a particle with a trajectory is excluded by the conceptualization employed.
This idea of the absolute square is important. It is how we get from the non-physical wavefunction to a real thing, even as abstract as probability. Why is the wavefunction non-physical? Because it has real and imaginary components: u = Re{u} + i*Im{u}, and nothing observed in nature has this feature. The absolute square of the wavefunction is real, and is obtained by multiplying the wavefunction by its complex conjugate u* = Re{u} - i*Im{u} (note the minus sign). Remembering that i*i = -1, you can see for yourself this is real. We'll come back to this. — Kenosha Kid
I believe the wave function, as you mention here, is artificial. It has been created in an attempt to establish consistency between the two incompatible representations of space, 1) massive bodies moving through empty space, and 2) energy moving as waves in space.
Notice, what you say later, that what makes the wave function "real" is the capacity for reversal. This is another feature of conventional conceptualization. We understand radiant energy, such as radiant heat, through its absorption, not through an understanding of the process of radiation. So this is a necessary condition of radiant energy, that it is absorbed. The concept of radiant energy is based in the absorption of energy into a body. Sure we can talk about something radiating energy into empty space, into an infinite vacuum or some such thing, but this is not consistent with the concept which is based in objects receiving energy, not in objects emitting energy.
This is a fundamental feature of our means of understanding, which is observation. The observer is always on the receiving end of the radiation, so our understanding of radiation is based in its reception. It doesn't really make sense to talk about observing radio wave emissions because the act of observing is itself a reception. And, though we can observe changes to the body which emits the radiation, this is not a true observation of emission itself. So, to facilitate mathematical calculations we simply assume that emission is an inversion of reception, and voila, the wavefunction is claimed to be real, but really there is a hole in the understanding here.
The back screen is a macroscopic object that cannot be treated precisely with quantum mechanics. — Kenosha Kid
I believe the macroscopic/microscopic division is not an adequate representation of the real divide. The real divide is the division between two incompatible conceptions of "space". One understanding of space is as a medium full of waves, and the other is as an empty vacuum with massive bodies moving around. You can see how the two conceptualizations are incompatible, and where the two conceptualizations meet, radiation is absorbed or emitted from a massive body, and there is confusion due to the incompatibility of the two. That the issue is not macroscopic/microscopic is evident from the fact that macroscopic things can be represented by the wave model. That the wave model representation of macroscopic objects is inaccurate is due to that hole in the understanding.
The back screen is a high-entropy object compared with the electron. That is, at any time, it may occupy one of hundreds of thousands or millions of microstates: particular configurations that are energetically equivalent to one another. At one instant t', a position on the screen r' may not admit an electron because it already has one there. At a subsequent instance t'', it might admit an electron at r'. The screen will explore these microstates in a thermodynamic way. i,e, in the same way that a box of gas will have different but energetically equivalent configurations of gas molecules one instant to the next. — Kenosha Kid
This is a good example of the incompatibility. You are describing the screen as an area of space within which there are subdivisions, some of which will allow for the existence of a particle. But the incoming radiation, to be absorbed into that space is being received as waves within this empty space. So it is necessary to have a transformation principle whereby space (as a medium) with energy moving as waves, is compatible with the conception of empty space with moving particles. Conventional wisdom tells us that the wave formulation is far more advanced, providing a much higher degree of understanding of the reality of the situation, so we ought to dispense this conception of empty space with bodies or particles moving around, and replace it with a consistent wave model. The whole idea described here, that the screen consists of an area with subareas which might or might not provide for the existence of a particle is the wrong approach. The entire area (screen, or macroscopic object) needs to be represented as an interaction of waves to be able to properly understand how the incoming waves of radiant energy will react. However, as I described above, the relationship between emission and reception of radiation is not well understood, and we cannot simply assume an inversion.
Because the electron's birth and death are the true boundary conditions of its wavefunction! — Kenosha Kid
This is the principal misleading, or misguided principle right here. If the radiant energy travels as waves, as necessitated by the concept "energy", the death of the electron is the moment that the energy is emitted. Its birth is when the energy is received. There is no continuity of the particle during transmission. The particle only exists as a part of a massive object. So this is where you need to turn your model around. You cannot represent a photon or electron as being emitted. The photon, as a particle only exists as a part of an object. If energy is emitted by that object, it is emitted as waves, and this constitutes the end of the photon or electron, not its beginning. Conversely, the beginning of the photon or electron, is when radiation is absorbed into an object. We must maintain these principles because the spatial conception which represents energy traveling from here to there, does not allow that energy travels as a particle, it necessitates waves. The particle only exists within the other spatial conception of objects existing in empty space. Remember, "boundary conditions" are applied as deemed required, so if you want your boundary conditions of the electron or photon to be true, you need to represent the true existence of the particle, as allowed for by the conceptions employed. If the conceptions deny the possibility of a particle transmitting energy from one object to another, you cannot employ boundary conditions of the particles, which allow that the particle exists while the energy is being transmitted as waves.
. -
 Kenosha Kid
3.2kI can say that the concepts employed here are deficient, showing a lack of understanding of the concepts. — Metaphysician Undercover
Kenosha Kid
3.2kI can say that the concepts employed here are deficient, showing a lack of understanding of the concepts. — Metaphysician Undercover
I welcome identification of any deficiencies. However, the concepts in question are those of non-relativistic and relativistic quantum mechanics, in which I have some background. Just to define some scope, which I had presumed implicit but perhaps is not, the question here is whether the insight gathered from Copenhagen interpretation regarding determinism is valid. This must be judged from within a quantum theory, with additions and subtractions of course, so I will focus on the parts of your response that fall within that scope.
A moving body has velocity, mass, and momentum according to Newtonian principles, but it does not have "energy". — Metaphysician Undercover
Oh dear god.
We understand radiant energy, such as radiant heat, through its absorption, not through an understanding of the process of radiation. — Metaphysician Undercover
Oh crikey!
I believe the macroscopic/microscopic division is not an adequate representation of the real divide. — Metaphysician Undercover
There is no cutoff, which is fine as I am not exploring the realm of the classical limit. It is sufficient to know that a classical limit exists. The relevance of the macroscopic screen is merely that it explores microstates, nothing more.
Conventional wisdom tells us that the wave formulation is far more advanced, providing a much higher degree of understanding of the reality of the situation, so we ought to dispense this conception of empty space with bodies or particles moving around, and replace it with a consistent wave model. — Metaphysician Undercover
This is worth treating. In 1900, things were thought to be either particles or waves. The blackbody radiation spectrum and quantised atomic orbitals turned that on its head: waves were behaving like particles; particles were behaving like waves. It was surprising, hence the "wave-particle duality paradox'.
There is no paradox. There is no preferred basis set for describing waves except for that of the operator a particular measurement device is described by. At one extreme, plane waves -- Eigenstates of the momentum operator -- have well defined momentum and no defined position, but occupy all of space. At the other, Eigenstates of the position operator have well-defined position but no defined momentum. Everything else lies in between.
The double-slit experiment begins with an electron with a well-defined position and, after measurement, ends with an electron with a well-defined position. These need not be precise, though they are typically treated as such. In between, the electron spreads out as a wave, but eventually must reduce, either deterministically or spontaneously, to something more localised. A good basis set that puts wavelike and particle-like extremes on equal footing is the stroboscopic wave-packet representation, on which I wrote my master's thesis. All of the above still holds: we simply replace Pauli exclusion of two electrons being in one kind of state (position) with that of two electrons being in another kind of state (stroboscopic wave-packet). The exclusion principle holds across all such bases (e.g. you cannot have two like-spin electron plane waves with the same momentum, which is what I had in mind for the states k, j', k" and k"', though these could be position, orbital, Bloch, Wannier or stroboscopic states or anything else you might consider, it makes no difference to the argument).
You cannot represent a photon or electron as being emitted. — Metaphysician Undercover
Stimulated emission. Spontaneous emission. Blackbody spectra. Photoelectric effect. Cathode ray tubes. Lasers. The concept of emission is pretty uncontroversial in quantum mechanics.
You obviously have some exotic ideas of your own about how nature is that are at odds with quantum mechanics. I would not try to dissuade you from them. The above is not meant as pro-quantum propaganda, but rather, as I said, to explore ideas within the field and assess their consequences for determinism. The end-game being an attempt to put to bed the 'quantum equals non-determinism' myth. Whether the concepts discussed are true or not is far less important than whether they hold or don't within that particular framework. -
 Harry Hindu
5.9k
Harry Hindu
5.9k
If the pattern is something that "builds up" then the pattern isn't the result of one electron, but many over time. One electron going through every ten seconds makes one dot on the screen every ten seconds that eventually builds up the pattern over time. So each electron behaves like a particle and the relationship between all the electrons is a wave, not that each electron is a wave, or else you'd get the pattern with the first electron. There would be no "building up" if each electron was a wave.If the voltage of the cathode is reduced such that only one electron fires out, say, per ten seconds, eventually the same pattern builds up. From this we deduce that each electron is a wave. — Kenosha Kid -
 Kenosha Kid
3.2kIf the pattern is something that "builds up" then the pattern isn't the result of one electron, but many over time. One electron going through every ten seconds makes one dot on the screen every ten seconds that eventually builds up the pattern over time. So each electron behaves like a particle and the relationship between all the electrons is a wave, not that each electron is a wave, or else you'd get the pattern with the first electron. There would be no "building up" if each electron was a wave. — Harry Hindu
Kenosha Kid
3.2kIf the pattern is something that "builds up" then the pattern isn't the result of one electron, but many over time. One electron going through every ten seconds makes one dot on the screen every ten seconds that eventually builds up the pattern over time. So each electron behaves like a particle and the relationship between all the electrons is a wave, not that each electron is a wave, or else you'd get the pattern with the first electron. There would be no "building up" if each electron was a wave. — Harry Hindu
I'm afraid not. If there are no other electrons to interfere with, and the electron does not interfere with itself, there is no possibility of interference effects. -
 Metaphysician Undercover
14.7kThis must be judged from within a quantum theory, with additions and subtractions of course, so I will focus on the parts of your response that fall within that scope. — Kenosha Kid
Metaphysician Undercover
14.7kThis must be judged from within a quantum theory, with additions and subtractions of course, so I will focus on the parts of your response that fall within that scope. — Kenosha Kid
There is a problem with this approach, and that is that you have outlined specific problems with quantum theory itself, and how these problems lead toward an appearance of indeterminism in some interpretations. To dispose of the appearance of indeterminism, the problems which are being interpreted need to be addressed themselves. Since the problems of quantum theory are a manifestation of the conceptualizations employed (as I described above), then we have to step outside quantum theory to get a handle on these problems.
That is why my Zeno analogy is relevant. What you are asking is analogous to saying let's adhere strictly to Zeno's descriptions, and try to solve Zeno's paradoxes from within that box. It cannot be done, because it is Zeno's descriptions themselves, the conceptualizations employed which are faulty, so we must step outside of those conceptualizations to locate their faults. How could we possibly judge the Copenhagen interpretation without stepping outside the descriptions and conceptualizations which are employed to produce it?
This is worth treating. In 1900, things were thought to be either particles or waves. The blackbody radiation spectrum and quantised atomic orbitals turned that on its head: waves were behaving like particles; particles were behaving like waves. It was surprising, hence the "wave-particle duality paradox'.
There is no paradox. There is no preferred basis set for describing waves except for that of the operator a particular measurement device is described by. At one extreme, plane waves -- Eigenstates of the momentum operator -- have well defined momentum and no defined position, but occupy all of space. At the other, Eigenstates of the position operator have well-defined position but no defined momentum. Everything else lies in between. — Kenosha Kid
This describes exactly what I explained. There are two distinct and incompatible conceptions of space. The wavefunction attempts to reconcile the two, but because they are incompatible it cannot. So the two defining parameters (boundaries if you like) of motion, 1)"well defined momentum and no defined position", and 2)"well defined position but no defined momentum", are each in themselves, incomprehensible if they are meant to describe an actual motion. The former describes the limits to the "wave in space" conception of space, and the latter describes the limits of the "particle in space" conception of space. The two conceptions are incompatible, so when attempts are made meld them together as the wave function, the result is uncertainty with respect to one or the other.
The double-slit experiment begins with an electron with a well-defined position and, after measurement, ends with an electron with a well-defined position. These need not be precise, though they are typically treated as such. In between, the electron spreads out as a wave, but eventually must reduce, either deterministically or spontaneously, to something more localised. — Kenosha Kid
Here again we have a demonstration of the two distinct, and incompatible spatial conceptions. You describe an electron as a particle with a well defined spatial position, at the beginning and at the end of the process. This represents the one spatial conception, "objects in space". In the meantime, the "in between", you say that the electron spreads out as a wave. This is a completely different conception of space, one in which there are "waves in space", and this conception of space is incompatible with the "objects in space" conception, as demonstrated by the Michelson-Morley experiments.
As I stressed in the last post, your claim that there is a particle, called an electron, which exists during the in between period, and "spreads out as a wave", is completely unsupported by the conceptualization of "energy". In fact, the concept of energy denies the possibility that there is such a particle. So your stated "beginning" is really the end of an electron, and your stated "end" is really the beginning of another electron, and what exists in between the two, providing for temporal continuity, is wave energy which is based in a conception of space that is incompatible with the conception of a particle as an object at a location in space.
It really makes no sense to attempt at a validation of a temporal continuity of a single electron by introducing different forms of the electron , like "stroboscopic wave-packet", when the real issue is that there are two distinct conceptions of space, one supporting the existence of particles like electrons, and the other supporting the existence of wave energy. Putting the two conceptions, wave-like and particle-like on equal footing is not a good idea because each of the two involves a conception of space which is incompatible with the other. Therefore the intelligent solution is to determine which of the two conceptions is superior to the other, and figure out what needs to be done to make things which are understood by the other, consistent. Pretending that the two can be made to appear consistent by putting them on an equal footing, is not a real solution.
The concept of emission is pretty uncontroversial in quantum mechanics. — Kenosha Kid
As your op describes, there are problems with quantum mechanics in general. Therefore we must question all principles, even those uncontroversial things which are taken for granted. The idea that emission can be described as spontaneous and random indicates that it is not well understood.
The end-game being an attempt to put to bed the 'quantum equals non-determinism' myth. — Kenosha Kid
OK, if that's what you want to discuss, then perhaps you can describe how spontaneous emission and random fluctuations are consistent with determinism. -
 Kenosha Kid
3.2kSince the problems of quantum theory are a manifestation of the conceptualizations employed (as I described above), then we have to step outside quantum theory to get a handle on these problems. — Metaphysician Undercover
Kenosha Kid
3.2kSince the problems of quantum theory are a manifestation of the conceptualizations employed (as I described above), then we have to step outside quantum theory to get a handle on these problems. — Metaphysician Undercover
I can see that you're keen to do so, but that is not a logical argument. The particular issue in question only occurs in one interpretation of QM, therefore it is not necessary to go outside of QM to avoid it, nor would I be saying much of anything about it if I did.
As I stressed in the last post, your claim that there is a particle, called an electron, which exists during the in between period, and "spreads out as a wave", is completely unsupported by the conceptualization of "energy". — Metaphysician Undercover
Perhaps in whatever exotic picture of the universe you have. In QM, it's quite a trivial affair. You define a wavefunction with a value of 1 at the initial position and 0 everywhere else as the initial state, and you time-evolve it according to its wave equation. It will disperse quite naturally.
It really makes no sense to attempt at a validation of a temporal continuity of a single electron by introducing different forms of the electron , like "stroboscopic wave-packet" — Metaphysician Undercover
An element of any basis set, such as the positional basis, can be written as a superposition in any other basis. In the case of the two extremes of position and momentum, this is simply the Fourier transform and its inverse.
OK, if that's what you want to discuss, then perhaps you can describe how spontaneous emission and random fluctuations are consistent with determinism. — Metaphysician Undercover
I dedicated quite a portion of the OP to spontaneous emission. -
 Harry Hindu
5.9k
Harry Hindu
5.9k
LOL. Just read what you wrote, bro.I'm afraid not. If there are no other electrons to interfere with, and the electron does not interfere with itself, there is no possibility of interference effects. — Kenosha Kid
You're saying the "beam" is wave and interferes with itself, so if an electron is a wave, then it can interfere with itself.A brief reminder: when a cathode fires electrons at a screen with two slits, beyond which is another screen, the pattern that builds up on the back screen is bands of light and dark, the dark bands being where few or no electrons strike, the light bands being where more strike. From this we deduce that the electron beam coming from the cathode is a wave.
If the voltage of the cathode is reduced such that only one electron fires out, say, per ten seconds, eventually the same pattern builds up. From this we deduce that each electron is a wave. — Kenosha Kid
A wave interfering with itself is how the pattern is created.
The "beam" is the relationship between the individual electrons and according to you is a wave. If the same pattern is created no matter how long the interval between each electron, then it isnt the electron that is a wave because one electron would create the pattern if it were a wave like the "beam" of electrons. -
 Kenosha Kid
3.2kLOL. Just read what you wrote, bro. — Harry Hindu
Kenosha Kid
3.2kLOL. Just read what you wrote, bro. — Harry Hindu
Ha!
The "beam" is the relationship between the individual electrons and according to you is a wave. If the same pattern is created no matter how long the interval between each electron, then it isnt the electron that is a wave because one electron would create the pattern if it were a wave like the "beam" of electrons. — Harry Hindu
Ah, I see the misunderstanding. I meant it as a chronological voyage of discovery. We conclude the beam is a wave from the interference pattern. We then go on to realise that each electron is a wave by reducing the voltage. Unclear, my bad. -
 Harry Hindu
5.9kYou're still missing the point.
Harry Hindu
5.9kYou're still missing the point.
All you did was reduce the interval between electrons being emitted and you get the same pattern. The beam is still there, just at a lower voltage, so it is still the beam that is the wave, and not individual electrons.
The second experiment doesn't show that each electron is a wave. It shows that electrons don't appear to move through, or are governed by, space-time like other particles, or maybe it is our view of space-time that is skewed. -
 Metaphysician Undercover
14.7kI dedicated quite a portion of the OP to spontaneous emission — Kenosha Kid
Metaphysician Undercover
14.7kI dedicated quite a portion of the OP to spontaneous emission — Kenosha Kid
Yes you described emission as the reversal of radiation. And I explained how this is an unjustified assumption. Your reply was "Oh crikey!". And then you went on to assert "the concept of emission is pretty uncontroversial in quantum mechanics." Now you refer back to the OP as if you think that the answer to my question is there. But all that is there is the following faulty assumption:
Photon emission/absorption is another example of a reversible process. — Kenosha Kid
You seem to be ignoring the fundamental facts of radiant energy. The ejection of an electron which is caused by the absorption of radiation, according to the photoelectric effect, or some other mechanism, what you call scattering, is not a simple reversal of the emission of radiation. The former has a determinate cause, the latter may be spontaneous. The fact that you can treat the two mathematically as one reversible process does not justify your claim that the two are one reversible process. -
 Kenosha Kid
3.2kThe former has a determinate cause, the latter may be spontaneous. — Metaphysician Undercover
Kenosha Kid
3.2kThe former has a determinate cause, the latter may be spontaneous. — Metaphysician Undercover
This is also treated in the OP.
The fact that you can treat the two mathematically as one reversible process does not justify your claim that the two are one reversible process. — Metaphysician Undercover
As I said, this is uncontroversial, and the purpose of the OP is not to compare QM with idiosyncratic theories. In QM, this obeys a specific symmetry of the universe that makes it reversible. -
 Kenosha Kid
3.2kThe second experiment doesn't show that each electron is a wave. It shows that electrons don't appear to move through, or are governed by, space-time like other particles, or maybe it is our view of space-time that is skewed. — Harry Hindu
Kenosha Kid
3.2kThe second experiment doesn't show that each electron is a wave. It shows that electrons don't appear to move through, or are governed by, space-time like other particles, or maybe it is our view of space-time that is skewed. — Harry Hindu
Maybe, but that does not fall within the scope of the OP, which concerns quantum mechanics, not alternative theories to quantum mechanics. -
 Harry Hindu
5.9k
Harry Hindu
5.9k
Sure it does. It shows that your OP is unfounded in asserting that electrons are waves, and is not the rest of your OP built upon that faulty premise?Maybe, but that does not fall within the scope of the OP, which concerns quantum mechanics, not alternative theories to quantum mechanics. — Kenosha Kid -
 Harry Hindu
5.9k
Harry Hindu
5.9k
Seems to me that you've admitted that consciousness is involved in some way to say that it has imaginary components, or where else in reality do imaginings exist? Is it me, or are scientists getting really lazy with their use of language?This idea of the absolute square is important. It is how we get from the non-physical wavefunction to a real thing, even as abstract as probability. Why is the wavefunction non-physical? Because it has real and imaginary components: u = Re{u} + i*Im{u}, and nothing observed in nature has this feature. — Kenosha Kid
If the wavefunction represents a fundamental characteristic of nature, then how can you say that nothing else observed in nature has this feature, when observing is what collapses the wavefunction? It's like saying that nothing else has the features of atoms when everything is made of atoms. You're simply talking about different views of the same thing - a view of atoms, waves and electrons from the macro-scale vs the micro-scale vs the quantum-scale. Each theory is simply a description made from one of these views. -
 Kenosha Kid
3.2kSure it does. It shows that your OP is unfounded in asserting that electrons are waves, and is not the rest of your OP built upon that faulty premise? — Harry Hindu
Kenosha Kid
3.2kSure it does. It shows that your OP is unfounded in asserting that electrons are waves, and is not the rest of your OP built upon that faulty premise? — Harry Hindu
As stated previously, the OP is regarding QM, and nothing outside that framework. Feel free to start a thread on the subject you'd obviously prefer to discuss. -
 Metaphysician Undercover
14.7k
Metaphysician Undercover
14.7k
I see, avoid the issue you claim to be addressing by asserting that the OP has already addressed it. I call that lying.
You propose a complete misrepresentation of the human conceptualization of radiant energy. Notice that a cooler object will not radiate heat to a warmer object, therefore contrary to your claim, emission/absorption is not a reversible process. Your claim that spontaneous emission is deterministic is dependent on this false premise. -
 Kenosha Kid
3.2kYou propose a complete misrepresentation of the human conceptualization of radiant energy. — Metaphysician Undercover
Kenosha Kid
3.2kYou propose a complete misrepresentation of the human conceptualization of radiant energy. — Metaphysician Undercover
I propose a rejection of the Copenhagen interpretation of quantum mechanics. Ideas about the nature of radiation that are different to quantum mechanics may well be fascinating, but not relevant. -
 fdrake
7.2kBoth the retarded wavefunction going from t -> t' and the advanced wave coming from t' -> t may explore whatever places they want, but only in the trajectories where one is the conjugate of the other do their trajectories become real. — Kenosha Kid
fdrake
7.2kBoth the retarded wavefunction going from t -> t' and the advanced wave coming from t' -> t may explore whatever places they want, but only in the trajectories where one is the conjugate of the other do their trajectories become real. — Kenosha Kid
Probably a stupid question: if the mapping from a wavefunction to it times its complex conjugate always produces a purely real variable, and that the "advanced wave" is defined by the mapping of this wavefunction to its complex conjugate, how could this be taken as evidence of a coincidence of physical mechanisms (two processes with the same result) when it's actually two names for the same mapping?
In other words; what generates the advanced wavefunction trajectories aside from the conjugation operation?
Analogy:
"By applying this new technique, we have transformed the sleeping agent into a soporific!"
"What did the technique add?"
"It reveals that it's no coincidence that sleeping agents are soporifics". -
 Kenosha Kid
3.2kProbably a stupid question: if the mapping from a wavefunction to it times its complex conjugate always produces a purely real variable, and that the "advanced wave" is defined by the mapping of this wavefunction to its complex conjugate, how could this be taken as evidence of a coincidence of physical mechanisms (two processes with the same result) when it's actually two names for the same mapping? — fdrake
Kenosha Kid
3.2kProbably a stupid question: if the mapping from a wavefunction to it times its complex conjugate always produces a purely real variable, and that the "advanced wave" is defined by the mapping of this wavefunction to its complex conjugate, how could this be taken as evidence of a coincidence of physical mechanisms (two processes with the same result) when it's actually two names for the same mapping? — fdrake
No, it's a good question. The first part of the answer is that they are both independently solutions to the relativistic wave equation. This is different to the non-relativistic Copenhagen interpretation, in which the advanced wave is not a solution at all, and really is just a mapping from the retarded wave. So just by solving the equation, you get forward and backward solutions.
The second part, which I mentioned but only in a throwaway fashion, is that we don't need to consider the 'hole' taking part in a given process to have the same (future) history as the electron's future. The birth and death of the particle are the two boundary conditions, but things like where the electron appears on the screen can be considered nodes. The advanced wave sent back to the cathode needn't be the same that conjugates the retarded wave beyond the the back screen.
A quick note on this... The OP is very much in the realm of QED, in which all processes really are reversible. If that was the end of it, we really would expect the advanced wave from death to birth to be the conjugate of the retarded wave from birth to death, and there would be no insight. Generally in TQM though, only the advanced wave from the screen to the cathode need conjugate with the electron, which is likely more general. There is no time-reversed equivalent of some electron-producing radioactive decays, for instance. -
 Metaphysician Undercover
14.7kIdeas about the nature of radiation that are different to quantum mechanics may well be fascinating, but not relevant. — Kenosha Kid
Metaphysician Undercover
14.7kIdeas about the nature of radiation that are different to quantum mechanics may well be fascinating, but not relevant. — Kenosha Kid
Your false claim that emission/absorption is reversible is obviously what is inconsistent with quantum physics.
And your refusal to accept the empirical evidence of a multitude of real examples of radiant energy, demonstrates that you are simply obsessed with some pet theory which is not supported by empirical evidence. -
 Kenosha Kid
3.2k
Kenosha Kid
3.2k
Visuals are not my strong suit, but I'm really trying :rofl: This is an oversimplified example of how, beyond the perfect symmetry of SR, retarded and advanced waves might not need to share the entirety of their histories, in this case in a scattering event.
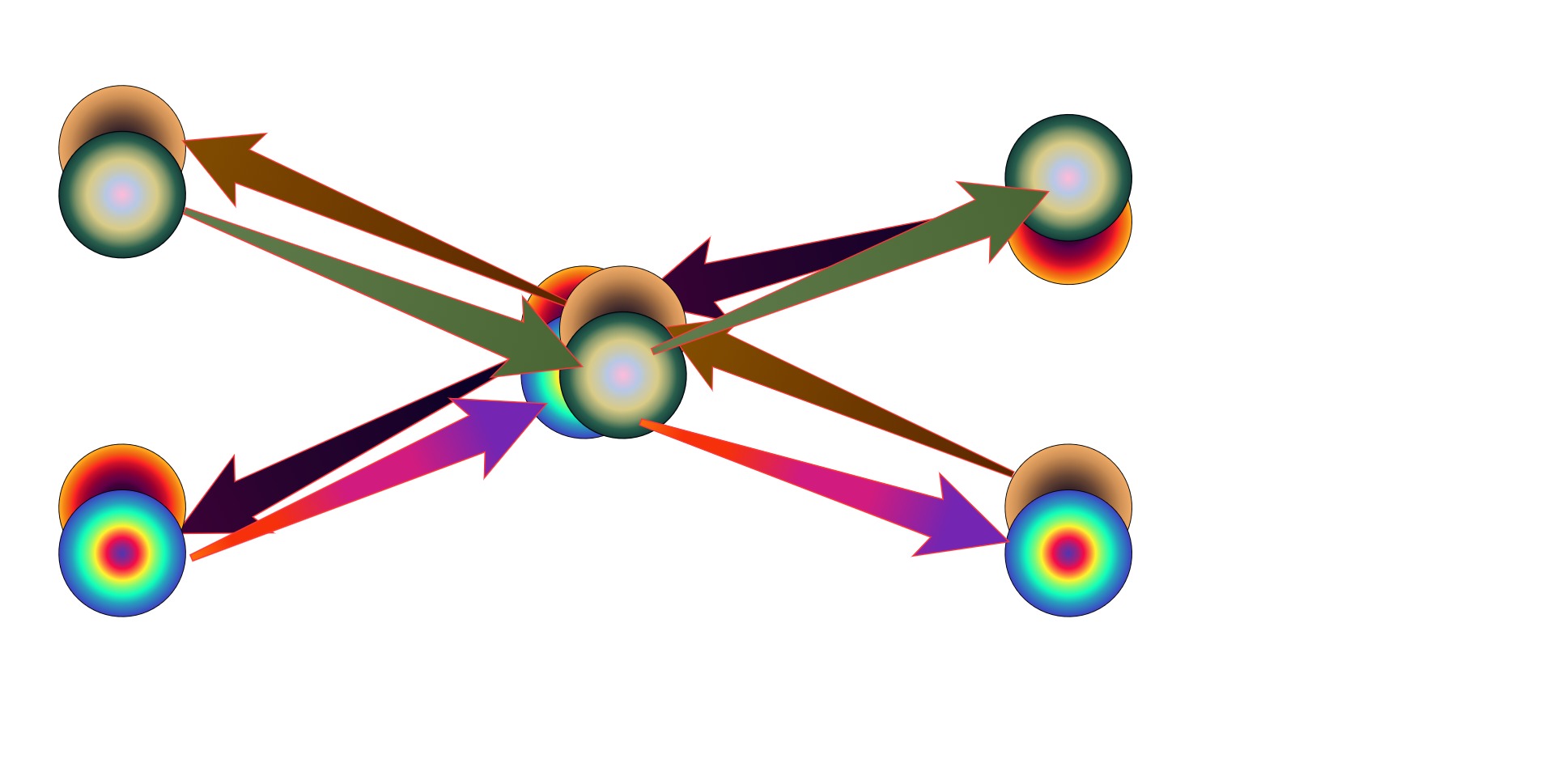
Time goes from left to right. -
 Harry Hindu
5.9k
Harry Hindu
5.9k
What is it that i obviously want to discuss, KK? The only thing that I've been discussing is the faulty assertions in your OP, but you can believe that I'm talking about something else if it makes sleep better tonight.As stated previously, the OP is regarding QM, and nothing outside that framework. Feel free to start a thread on the subject you'd obviously prefer to discuss. — Kenosha Kid -
 Kenosha Kid
3.2kWhat is it that i obviously want to discuss, KK? — Harry Hindu
Kenosha Kid
3.2kWhat is it that i obviously want to discuss, KK? — Harry Hindu
Something wherein electrons are not waves, i.e. something that is not quantum mechanics. And by all means, but elsewhere. -
 Gregory
5khttps://en.wikipedia.org/wiki/Special_relativity_(alternative_formulations)
Gregory
5khttps://en.wikipedia.org/wiki/Special_relativity_(alternative_formulations)
https://en.wikipedia.org/wiki/Alternatives_to_general_relativity
Not much agreement in science it seems. -
 Harry Hindu
5.9kSomething wherein electrons are not waves, i.e. something that is not quantum mechanics. And by all means, but elsewhere. — Kenosha Kid
Harry Hindu
5.9kSomething wherein electrons are not waves, i.e. something that is not quantum mechanics. And by all means, but elsewhere. — Kenosha Kid
You're confused. Its your OP that fails to show that electrons are waves. You've only been able to show that the beam is a wave. So if a requirement of QM is a belief that electrons are waves, then your OP isn't about QM either. That's all I'm saying. -
 jgill
4kMy best friend for over forty years was once a physics major, but he switched to math after taking an introductory course in quantum theory. He became a highly regarded math professor. My father had a masters in math, then took a course in topology one summer in the 1930s at the U of Michigan. He then left math to become a business statistician.
jgill
4kMy best friend for over forty years was once a physics major, but he switched to math after taking an introductory course in quantum theory. He became a highly regarded math professor. My father had a masters in math, then took a course in topology one summer in the 1930s at the U of Michigan. He then left math to become a business statistician.
There seems to be a point in an academic progression at which a student may get into a course in his area that is an abrupt excursion into something that seems weird and unlike anything he has encountered before. If he is fortunate and has a really good prof he may become enthusiastic and proceed, or, more likely, he may have an indifferent prof and exit the discipline. My own experience was a beginning grad course in set theory. It could have come close to leveraging me out of math, but the young, energetic prof made it both interesting and pleasantly challenging. I never returned to the subject, but I stayed in the discipline.
I had a year of physics, planning to become a physicist - but reading about quantum theory showed me the error of my thinking! Hats off to Kenosha Kid. :up: -
 Kenosha Kid
3.2kYou're confused. Its your OP that fails to show that electrons are waves. You've only been able to show that the beam is a wave. So if a requirement of QM is a belief that electrons are waves, then your OP isn't about QM either. That's all I'm saying. — Harry Hindu
Kenosha Kid
3.2kYou're confused. Its your OP that fails to show that electrons are waves. You've only been able to show that the beam is a wave. So if a requirement of QM is a belief that electrons are waves, then your OP isn't about QM either. That's all I'm saying. — Harry Hindu
The OP is not deriving QM, merely summarising it. Conversation would be pretty limited in scope if you have to re-derive from first principles everything that you intend to discuss every time. -
 Kenosha Kid
3.2kHats off to Kenosha Kid. — jgill
Kenosha Kid
3.2kHats off to Kenosha Kid. — jgill
Thanks jgill! Math is much harder, I think. My department didn't offer a general relativity course when I was an undergraduate, so I had to sit in on the math department's course to learn about it. Hands down the hardest time I had at uni. Although fluid dynamics comes a close second. Kudos to your friend.
Welcome to The Philosophy Forum!
Get involved in philosophical discussions about knowledge, truth, language, consciousness, science, politics, religion, logic and mathematics, art, history, and lots more. No ads, no clutter, and very little agreement — just fascinating conversations.
Categories
- Guest category
- Phil. Writing Challenge - June 2025
- The Lounge
- General Philosophy
- Metaphysics & Epistemology
- Philosophy of Mind
- Ethics
- Political Philosophy
- Philosophy of Art
- Logic & Philosophy of Mathematics
- Philosophy of Religion
- Philosophy of Science
- Philosophy of Language
- Interesting Stuff
- Politics and Current Affairs
- Humanities and Social Sciences
- Science and Technology
- Non-English Discussion
- German Discussion
- Spanish Discussion
- Learning Centre
- Resources
- Books and Papers
- Reading groups
- Questions
- Guest Speakers
- David Pearce
- Massimo Pigliucci
- Debates
- Debate Proposals
- Debate Discussion
- Feedback
- Article submissions
- About TPF
- Help
More Discussions
- Biological Determinism As The Fundamental Pedagogy of National Socialist Thought (Half of Chapter 1)
- Biological Determinism As The Fundamental Pedagogy of National Socialist Thought
- The Consequences of Belief in Determinism and Non-determinism
- Are we doomed to discuss "free will" and "determinism" forever?
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum






