-
 Shawn
13.5kFollowing are exerts from Susan Haack's, Philosophy of Logics. A good book by all means.
Shawn
13.5kFollowing are exerts from Susan Haack's, Philosophy of Logics. A good book by all means.
Monism states that there is just one correct system of logic.
Pluralism states that there is more than one correct system in logic.
Instrumentalism states that there is no "correct" logic; the notion of correctness is inappropriate.
Below is a schematic from the book that might serve as a mental template differentiating between the three versions of the metaphysical and epistemological questions about logic:
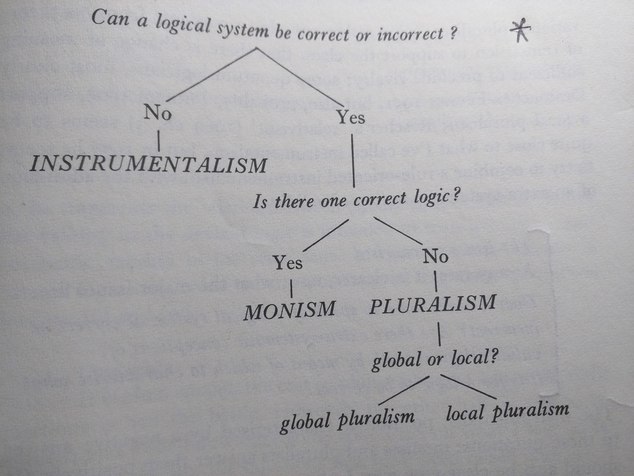
First, some comments about the conception of correctness which both monism and pluralism require: this conception depends upon a distinction between system-relative and extra-systematic validity/logical truth; roughly, a logical system is correct if the formal arguments which are valid in that system correspond to informal arguments which are logically true in the system correspond to statements which are logically true in the extra-systematic sense. The monist holds that there is a unique logical system which is correct in this sense, the pluralist that there are several.
The point is that the difference between a pluralism which admits classical logic and its extensions (or a deviant logic and its extensions) as both correct systems of logic, and a monism which admits both classical logic and its extensions (or a deviant logic and its extensions) as both fragments of the correct system of logic, is only verbal.
The instrumentalist position results from a rejection of the idea of the 'correctness' of a logical system, an idea idea accepted by both monists and pluralists.
An instrumentalist will only allow the 'internal' question, whether a logical system is sound, whether that is all and only the theorems/syntactically valid arguments of the system are logically true/valid in the system.
An illustration is the meaning-variance thesis proposed by Feyerabend's, which states: that the meanings of theoretical terms in science depend upon the theories in which they occur, so that there is failure of rivalry between alternative, apparently competing, scientific theories.
Another version of instrumentalism seems to derive from a refusal to apply any idea of truth, even a system-relative idea, to logic. Logic, it is argued, is not to be thought of as a set of statements, as a theory to be assessed as true or false; rather, it is to be thought of as a set of rules or procedures, to which the concepts of truth and falsity simply don't apply.
The issues summarized:
Does it make sense to speak of a logical system as correct or incorrect? Are the extra systematic conceptions of validity/logical truth by means of which to characterize what it is for a logic to be correct?
Furthermore,
Must a logical system aspire to global application i.e. to represent reasoning irrespective of subject matter, or may a logic be locally correct, i.e. correct within a limited area of discourse?
So, upon becoming acquainted or re-acquainted with the following types of metaphysical statements about logic, as to whether there's just one correct logical system, or a plurality of them, or even the irrelevance of the question manifest in instrumentalism, what would you answer in the poll?-
Monism. Pluralism.100%Instrumentalism.0%
-
Monism.
-
 Janus
17.9kMonism states that there is just one correct system of logic.
Janus
17.9kMonism states that there is just one correct system of logic.
Pluralism states that there is more than one correct system in logic.
Instrumentalism states that there is no "correct" logic; the notion of correctness is inappropriate. — Posty McPostface
What does "correct" mean in relation to logics? Does it mean 'consistent' or 'true'? There is certainly more than one kind of logic. A logic is a methodology of thought, and it would not seem to make sense to say that you could have a methodology without internal consistency. If truth is the criterion of "correctness" then you would need to explain what it could mean for a logic to be true. Logical arguments are judged according to their validity; whether they are true actually has nothing to do with the logic at all.
So I would agree that the notion of correctness is inappropriate if correctness is understood to be equivalent to truth, but it would not seem to be inappropriate if correctness is understood to correspond to internal consistency. I would say pluralism is the right choice, and that pluralism is not inconsistent with instrumentalism, because a logic would fail to be instrumental if it lacked methodological consistency.
Although having said that instrumentalism is right only insofar as it rejects the idea that correctness means truth. If it accepts that correctness means methodological consistency then it is false to say that the notion of correctness is inappropriate, even though to say under that assumption that correctness is appropriate would seem to be a trivial truism. -
 Shawn
13.5kWhat does "correct" mean in relation to logics? — Janus
Shawn
13.5kWhat does "correct" mean in relation to logics? — Janus
Yes, I take it as internally consistent here, and if that follows, then true and valid.
There is certainly more than one kind of logic. — Janus
Yes, there is, what's your point?
A logic is a methodology of thought, and it would not seem to make sense to say that you could have a methodology without internal consistency. — Janus
According to the instrumentalist yes, and global pluralist.
If truth is the criterion of "correctness" then you would need to explain what it could mean for a logic to be true. — Janus
Internal consistency does that for you, or 'logic takes care of itself'.
So I would agree that the notion of correctness is inappropriate if correctness is understood to be equivalent to truth, but it would not seem to be inappropriate if correctness is understood to correspond to internal consistency. — Janus
Both go along together I suppose, depending on whether your a monist, pluralist and even an instrumentalist. So, yeah, we're talking about tautologies. I think this is me speaking as a monist.
I would say pluralism is the right choice, and that pluralism is not inconsistent with instrumentalism, because a logic would fail to be instrumental if it lacked methodological consistency. — Janus
I agree.
Although having said that instrumentalism is right only insofar as it rejects the idea that correctness means truth. If it accepts that correctness means methodological consistency then it is false to say that the notion of correctness is inappropriate, even though to say under that assumption that correctness is appropriate would seem to be a trivial truism. — Janus
Not that trivial. Again, speaking as a monist, I think. -
 Shawn
13.5kOne thought that bugs me is that if Godel disproved the internal consistency of any finite logical system to be self proving, and thus requires extra-systematic appeals to another logical system to validate proofs or wff statements. If, so, then we are indeed left with, I think, either instrumentalism or local pluralism. Asserting monism in this case is possible, but meaningless.
Shawn
13.5kOne thought that bugs me is that if Godel disproved the internal consistency of any finite logical system to be self proving, and thus requires extra-systematic appeals to another logical system to validate proofs or wff statements. If, so, then we are indeed left with, I think, either instrumentalism or local pluralism. Asserting monism in this case is possible, but meaningless.
Yes? -
 Wayfarer
26kMonism states that there is just one correct system of logic. — Posty McPostface
Wayfarer
26kMonism states that there is just one correct system of logic. — Posty McPostface
I think I could take issue with this, as I think that the whole idea is extrapolated from 'monotheism'. This is the idea that there is but 'one true God', and that, by implication, other gods, and non-theistic philosophies, are incorrect.
I mean, if you think back to Aristotelian logic, I don't think it is said that there is 'one correct system of logic', although I suppose it might be an implicit meaning.
But I think this approach tends to blur the lines between epistemology and metaphysics. I think you can uphold a logically rigorous outlook, without having to say that there is only one correct system of logic. I suppose you would be saying that some propositions are logical and some are not, but whether that amounts to an assertion about there being 'one system of logic', I'm not sure. -
 Janus
17.9kYes, I take it as internally consistent here, and if that follows, then true and valid. — Posty McPostface
Janus
17.9kYes, I take it as internally consistent here, and if that follows, then true and valid. — Posty McPostface
The thing is that logical arguments, when consistent and when the conclusions are "contained in" the premises, are said to be valid. The validity of arguments, though, say nothing about their truth. The truth of an argument depends on the soundness of its premises.
So, that's why I think it is inappropriate to apply the notion of truth to logics, because logic in general is not about truth but about validity. But then maybe I misunderstood you, maybe you want to ask the "ontological" question about logic; whether logic(s) "reflect(s) reality", or something like that? If that is accepted as a coherent question, then I suppose the question as to whether there is more than one logic which reflects reality could be asked. Is it a coherent question, though? -
 Shawn
13.5kBut then maybe I misunderstood you, maybe you want to ask the "ontological" question about logic; whether logic(s) "reflect(s) reality", or something like that? If that is accepted as a coherent question, then I suppose the question as to whether there is more than one logic which reflects reality could be asked. Is it a coherent question, though? — Janus
Shawn
13.5kBut then maybe I misunderstood you, maybe you want to ask the "ontological" question about logic; whether logic(s) "reflect(s) reality", or something like that? If that is accepted as a coherent question, then I suppose the question as to whether there is more than one logic which reflects reality could be asked. Is it a coherent question, though? — Janus
Yes, that was the question. I'm not sure how one goes about proving or surmising it. Hence, why I brought up Godel. Is this one of those, whereof one cannot speak, thereof one ought remain silent, moments? -
 Shawn
13.5kProofs within P are perfectly good - no need for "extra-systematic appeals" to anything. — tim wood
Shawn
13.5kProofs within P are perfectly good - no need for "extra-systematic appeals" to anything. — tim wood
Yes, but, when one goes about trying to prove truths within any sufficiently complex formal system, then one will run into cases where such proofs are unobtainable within that very formal system, according to Godel. Hence, a new extra-systematic system must be incorporated, and hence, monism fails, and pluralism prevails, or even instrumentalism. -
 Janus
17.9kIs this one of those, whereof one cannot speak, thereof one ought remain silent, moments? — Posty McPostface
Janus
17.9kIs this one of those, whereof one cannot speak, thereof one ought remain silent, moments? — Posty McPostface
Now, that's hard to say!
Welcome to The Philosophy Forum!
Get involved in philosophical discussions about knowledge, truth, language, consciousness, science, politics, religion, logic and mathematics, art, history, and lots more. No ads, no clutter, and very little agreement — just fascinating conversations.
Categories
- Guest category
- Phil. Writing Challenge - June 2025
- The Lounge
- General Philosophy
- Metaphysics & Epistemology
- Philosophy of Mind
- Ethics
- Political Philosophy
- Philosophy of Art
- Logic & Philosophy of Mathematics
- Philosophy of Religion
- Philosophy of Science
- Philosophy of Language
- Interesting Stuff
- Politics and Current Affairs
- Humanities and Social Sciences
- Science and Technology
- Non-English Discussion
- German Discussion
- Spanish Discussion
- Learning Centre
- Resources
- Books and Papers
- Reading groups
- Questions
- Guest Speakers
- David Pearce
- Massimo Pigliucci
- Debates
- Debate Proposals
- Debate Discussion
- Feedback
- Article submissions
- About TPF
- Help
More Discussions
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum





