It says right in the OP, " Sleeping Beauty volunteers to undergo the following experiment and is told all of the following details." That is the first line of the problem. — Jeremiah

Sorry. Don't remember reading that. I brought up the issue before.

I just gave you my response and I am not going to wade through your clear misunderstanding of Lewis's argument. — Jeremiah

You're mistaken. (L6) P+(Heads) = 2/3 is a consequence of Lewis' halfer argument and it contradicts Elga's (E1) P+(Heads) = 1/2. As Lewis says:

"I reject Elga's premiss: my (L6) contradicts his (E1)."

You are not paying attention to what the plus means, where it shows up and where it doesn't show up.

But if your selected door does not have the car behind it then it is very relevant information, because it means the car is behind the remaining closed door that you did not select. — andrewk

You are confusing information with theatrics.

The Monty Hall problem and its analysis is identical to choosing 1 door, or choosing 2 doors. There is no more to it than that.

Yes. Your initially chosen door has 1/3 probability of containing the prize. The other two doors have a total of 2/3 probability. When the host shows you that one of those doors is empty, its probability goes to 0. — Andrew M

We're getting there. If the host instead told you that he could see that behind one of the other two doors, there was nothing. Do you think he is telling you something you don't already know for certain?

Would you still swap to choosing 2 doors, or stick with your initial choice of 1.

It's the same problem, with identical results, just without the sleight of hand.

The Monty Hall problem and its analysis is identical to choosing 1 door, or choosing 2 doors. — tom

Yes, if you switch you are effectively choosing two doors, which leads to the accepted solution that it is optimal to switch. That's what I said above.

Perhaps I misunderstood your post. It appeared to me from your statement that you've never met anybody that agrees with you on this, that you were rejecting the accepted solution. If you were, I'd be interested to know why. If not, there's nothing to disagree on.

We have P(C) = 1/3. If you retain your selection then the probability of a win is:

1/3 x P(win | C & not switch) + 2/3 x P(Win | ~C & not switch) = 1/3 x 1 + 2/3 x 0 = 1/3.

On the other hand if you switch the probability of a win is:

1/3 x P(win | C & switch) + 2/3 x P(Win | ~C & switch) = 1/3 x 0 + 2/3 x 1 = 2/3. — andrewk

It's 1/2 if you switch. I ran the experiments:

Here's the result of 100,000 games where you don't re-guess. 1/3 games are winners

Here's the result of 100,000 games where you re-guess. 1/2 games are winners

Go down towards the bottom and hit "Execute".

Edit: Actually, the logic of the 1/2 winners was wrong. It doesn't switch doors but reselects at random. I'll redo it.

You (and @tom) were right. 2/3.

The probability tree on the Monty Hall Wikipedia page can be used to explain why I disagree about the Sleeping Beauty problem:



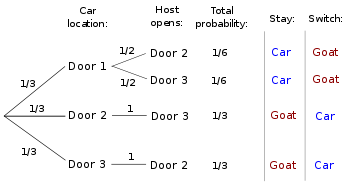
Ignore the bottom branch and treat the first two as Tails and Heads respectively each with probability 1/2. The Tails branch splits into 1st awakening and 2nd awakening (we're using my amended scenario where there's no mention of days) each with probability 1/2. The Heads branch extends to 1st awakening with probability 1. Using the multiplication rule as used in the above tree, we get Tails + 1st awakening = 1/4, Tails + 2nd awakening = 1/4, and Heads + 1st awakening = 1/2.

What I don't understand is why one would add a 2nd awakening branch to the Heads branch (and giving it a probability of 1/2?) if we know that in our experiment a flip of heads never offers a 2nd awakening. After all, we wouldn't add Door 1 or Door 2 as branches from the Door 2 branch because we know the rules prohibit such an event.

Here's some Monty Hall code in R
Under this code the prob of winning under no-switch is about 1/3 and 2/3 if the contestant switches.

It's the same problem, with identical results, just without the sleight of hand. — tom

Yes, the host's information is irrelevant if you can just switch to the other two doors instead of specifying a particular door number.

One thought here is that you could use a similar tree structure to argue for a quarter probability for heads. The first two branches represent the first and second awakenings with 1/2 probability each. The first awakening branch splits into heads and tails branches with 1/2 probability each. The second awakening branch extends to a tails branch with probability 1. Multiplying, we get first awakening + heads = 1/4, first awakening + tails = 1/4, second awakening + tails = 1/2.

Now those first two branch probabilities don't seem particularly plausible since there are twice as many first awakening states. But the same can be said for the halfer view since there are twice as many tail states.

One thought here is that you could use a similar tree structure to argue for a quarter probability for heads. The first two branches represent the first and second awakenings with 1/2 probability each. The first awakening branch splits into heads and tails branches with 1/2 probability each. The second awakening branch extends to a tails branch with probability 1. Multiplying, we get first awakening + heads = 1/4, first awakening + tails = 1/4, second awakening + tails = 1/2. — Andrew M

The probability of the awakenings is dependent on the coin flip (1st awakening is 1 if heads, 0.5 if tails), whereas the probability that a coin flip lands heads is independent. So I would say my branching makes sense whereas yours doesn't.

Or am I misunderstanding this?

Now those first two branch probabilities don't seem particularly plausible since there are twice as many first awakening states. But the same can be said for the halfer view since there are twice as many tail states. — Andrew M

I don't understand why the number of states matters. I roll a dice with 3 red faces, 2 blue faces, and 1 white face. I give you a ball with the colour of the face that the roll lands on. There might be three states (red, blue, or white ball), but the odds aren't 1/3 each. What matters are the probabilities that lead up to that state. A 1/2 probability leads to the red ball state, a 1/3 probability leads to the blue ball state, and a 1/6 probability leads to the white ball state.

If I run this experiment and give you one of the balls, hidden in a box, you don't just think "well, it could be one of any three colours, and there's no distinguishing feature in my current state to suggest that it's one rather than the others, so it's 1/3 chance of being red". Instead you think "well, the initial dice roll gave 1/2 odds of red, so it's 1/2 odds of red".

So why not apply the same reasoning to Sleeping Beauty? The initial coin toss has 1/2 odds of heads, so it's 1/2 odds of heads.

And to continue the analogy, let's say that I let you guess twice in the case that it's not a red ball. What's the smarter guess? Obviously to guess that it isn't red, because if you're right then you're right twice. If we record these winnings then we can see that you were right 2/3 of the time. But that doesn't mean that there was a 1/3 chance of getting a red ball. Introducing an element of amnesia in between the two guesses doesn't change that.

Also relevant is the question I asked earlier: if we have two theories – one which posits a single world and one which posits multiple worlds – should our credence favour the theory which posits multiple worlds? There are more states in which we're in one of multiple worlds than in which we're in the only world. Is that what matters?

I believe this is a disagreement between the self-sampling assumption and the self-indication assumption.

P(Heads|Awake) = (P(Heads) * P(Awake|Heads)) / P(Awake) = (1/2 * 1/2) / 3/4 = 1/3

There are four equally probable states in the experiment, three awake states and one sleep state, so P(Awake) = 3/4 and P(Awake|Heads) = 1/2. — Andrew M

This is why I suggested the alternative experiment where we don't talk about days at all and just say that if it's heads then we'll wake her once (and then end the experiment) and if it's tails then we'll wake her twice (and then end the experiment). There aren't four equally probable states in the experiment.

So we either say that P(Awake) = 1 (and/)or we say that being awake doesn't provide Beauty with any information that allows her to alter the initial credence that P(Heads) = 0.5.

Tuesdays and Heads is clearly and obviously not in the sample space. It is not a possible outcome, she will be never be interviewed on Heads and Tuesday.

But that doesn't mean that there was a 1/3 chance of getting a red ball. — Michael

This is not what the question is about. The question is whether there's 1/3 chance of being questioned as a result of getting a red ball.

This is why I suggested the alternative experiment where we don't talk about days at all and just say that if it's heads then we'll wake her once (and then end the experiment) and if it's tails then we'll wake her twice (and then end the experiment). There aren't four equally probable states in the experiment. — Michael

There's still the fourth state of it being the time you'd be awakened the second time and heads was thrown.

If I throw heads I choose a random person to question. If I throw tails I choose 7 599 999 999 people to question. You find yourself to be a part of the experiment, and don't have any knowledge on whether other people were chosen.

What are the odds you're a part of the experiment because heads was thrown?

You’re inventing a state that doesn’t exist in the experiment, and despite the rules of the experiment you’re asserting it to be equally probable.

Also, the time of the awakening(s) is random.

That’s similar to the question I asked here.

But to address your question, it’s a false comparison. In this case the probability that you’re asked if heads is one in billions, whereas in Beauty’s case the probability is one. You need an example where you’re guaranteed to be asked whatever the result.

What about if I’m asked in either case but don’t know if I’m first or second or third (and so on) in the case of tails? There might be multiple states for tails but I’d still say my credence should be 0.5.

Actually it's almost exactly 50%. But what you're saying is that if we choose random people to the test for each questioning instead of waking up the same person, then the answer is 1/3?

No, it’s a half. Where’d you get 1/3?

So it's not a false comparison because the answer is still 1/2?

This is where I’m guaranteed to be asked either way. In your example I’m not guaranteed to be asked, which is why it’s a false comparison.

You're not guaranteed to be asked if random people are chosen for the questioning either.

I’m saying that if it’s heads then only I’m asked and if it’s tails then I’m asked and 1,000 other people are asked. This is a better comparison than your example where I’m not guaranteed to be asked.

I’m saying that if it’s heads then only I’m asked and if it’s tails then I’m asked and 1,000 other people are asked. — Michael

That's not how it works, it needs to be a random person chosen for the situation to be comparable. The Sleeping Beauties at different scenarios are comparable to separate persons because of the amnesia, except arguably the Monday versions, who however don't have the knowledge it's Monday, unlike you, who always has the knowledge you are you.

Sleeping Beauty is guaranteed to be asked, and she knows it. To make it (more) comparable I have to know that I’m guaranteed to be asked, but not know whether I’m the person asked on Monday or the person asked on Tuesday. In your example I know that I’m almost guaranteed to be asked if it’s tails and almost guaranteed not to be asked if it’s heads, and that’s an incomparable difference.

Sleeping Beauty knows she has 1/2 chance of going through any possibility. You have 1/2 chance of going through Monday+heads on 1/4 chance of going through each tails outcome. Those situations are not comparable.

Sleeping Beauty knows she has 1/2 chance of going through any possibility. You have 1/2 chance of going through Monday+heads on 1/4 chance of going through each tails outcome. Those situations are not comparable. — BlueBanana

If there's a 1/4 chance that I'm being asked on Tuesday then there's a 1/4 chance that if I'm Sleeping Beauty being interviewed right now then today is Tuesday.

Notice how you've decided (correctly) not to consider Heads + Tuesday and argue that in my example there's a 1/3 chance of it being heads. Why the inconsistency? Is the fallacy of considering Heads + Tuesday as a state in the experiment more evident in my example than the Sleeping Beauty example?

Although the main point I've been arguing here is that your example isn't at all comparable. In Sleeping Beauty's case there's a probability of 1 that she will be asked if the coin lands heads and a probability of 1 that she will be asked if the coin lands tails, whereas in your case there's a probability of 1/7.5 billion that I will be asked if the coin lands heads and a probability of 7.49 billion/7.5 billion that I will be asked if the coin lands tails. That makes all the difference and is why the cases are incomparable.