-
 Tarskian
658Most mathematical truth is unprovable and therefore unpredictable, if only because most of its truth is ineffable ("inexpressible"). It is easy to get the wrong impression that mathermatical truth would be orderly.
Tarskian
658Most mathematical truth is unprovable and therefore unpredictable, if only because most of its truth is ineffable ("inexpressible"). It is easy to get the wrong impression that mathermatical truth would be orderly.
https://en.wikipedia.org/wiki/Mathematical_beauty
Mathematical beauty is the aesthetic pleasure derived from the abstractness, purity, simplicity, depth or orderliness of mathematics.
This impression is based on our inability to "see" most of its chaotic truth because it is ineffable. It is simply invisible to us. Furthermore, we even fail to see its otherwise visible chaos, because our methods mostly fail to reach it.
In his paper, "True but unprovable", Noson Yanofsky focuses on explaining why most mathematical truth cannot be expressed in language:
http://www.sci.brooklyn.cuny.edu/~noson/True%20but%20Unprovable.pdf
There are more true but unprovable statements than we can possibly imagine.
We have come a long way since Gödel. A true but unprovable statement is not some strange, rare phenomenon. In fact, the opposite is correct. A fact that is true and provable is a rare phenomenon. The collection of mathematical facts is very large and what is expressible and true is a small part of it. Furthermore, what is provable is only a small part of those.
The world of mathematical truth does not look like most people believe it does. It is not orderly. It is fundamentally unpredictable. It is highly chaotic. -
 Joshs
6.7k
Joshs
6.7k
The world of mathematical truth does not look like most people believe it does. It is not orderly. It is fundamentally unpredictable. It is highly chaotic — Tarskian
I’m not sure what ‘true’ as ineffability is supposed to mean here in the context of chaos and unpredictability. Could you say a little more about what makes an unprovable mathematical proposition true? I’m sure you wouldnt want to argue that the infinite task of ensconcing smaller axiomatic systems within more encompassing axiomatic systems involves a qualitative change of sense of meaning that prevents us from attributing all these systems to the same truth, and therefore one is not in fact dealing with an already defined infinity, but with a finite task whose sense is continually shifting . This would be Wittgenstein’s view, which i agree with. But I am guessing you would argue alongside Godel and Yanofsky that every iterative subsuming of axiomatic system within axiomatic system belongs to the same ‘truth’. -
 Banno
30.6kWhy should we suppose that natural languages are only countably infinite?
Banno
30.6kWhy should we suppose that natural languages are only countably infinite?
Consider:
A convolute argument, perhaps, but it shows that one must do more than simply assert that natural languages are at most countably infinite. Yanofsky must argue his case. " ...the collection of all properties that can be expressed or described by language is only countably infinite because there is only a countably infinite collection of expressions" begs the question. Indeed, the argument above shows it to be questionable.1. Let L be the NL English.
2. The set S0 is contained in L, where
S0= {Babar is happy; I know that Babar is happy; I know that I know that Babar is happy; . . .}
3. S1 may be constructed as follows
a. Form the set of all subsets of S0, P(S0).
b. For each element B in P(S0), form the sentence that is the coordinate conjunction of all the sentences in B.
c. Let S1 be the collection of all sentences formed in (3b).
S1 = {Babar is happy; I know that' Babar is happy; I know that I know that Babar is happy; ... ; Babar is happy and I know that Babar is happy; Babar is happy and I know that I know that Babar is happy;... ;Babar is happy, I know that Babar is happy, and I know that I know that Babar is happy;...}
4. S0 is denumerable, but S1, which is equinumerous with P(S0) is not denumerable (by Cantor's Theorem).
5. S2, S3, etc., can be constructed analogously. Each successive S has a greater transfinite cardinality than the one preceding it.
6. All of the S collections are contained within L.
7. L has no fixed cardinality. — The Vastness of Natural Language
There is something very odd about an argument, in a natural language, that claims to place limits on what can be expressed in natural languages. -
 Tarskian
658He attributes to Godel this idea:
Tarskian
658He attributes to Godel this idea:
:“'Basic arithmetic cannot prove a contradiction.' — tim wood
The paper actually says:
As a bonus, Gödel described another interesting statement in the language of basic arithmetic. He was able to formulate a statement in basic arithmetic that says:
“Basic arithmetic cannot prove a contradiction.”
So, it only insists that the sentence "PA cannot prove a contradiction" can be expressed in PA itself.
In the following paper, containing a version of the proof, the author expresses it by reifying the truth value for falsehood (⊥):
http://sammelpunkt.philo.at/id/eprint/2676/1/Bagaria.pdf
page 12:
Let CON(T) be the sentence ¬BewT(Í⊥Î). Thus, CON(T) says, via coding, that T is consistent.
In another paper, with another version of the proof, the author insist that it is enough to express the unprovability of any arbitrary falsehood. No need to reify truth values:
http://www.sfu.ca/~kabanets/308/lectures/lec11.pdf
We say that a proof system P is consistent if P does not prove both A and ¬A for some sentence A. That is, a consistent proof system cannot derive a contradiction A ∧ ¬A. In the case of a proof system P for arithmetic, we get that P is consistent iff P does not prove the sentence “1 = 2” (since 1 6 = 2 can be derived in P by the usual axioms (of Peano arithmetic) for the natural numbers).
ConsP : “the sentence “1 = 2” is not provable in P ”
So, in that case, let's consP be the sentence ¬BewP(Í1 = 2Î).
But then again, it is also perfectly possible to express the notion of consistency in full -- straight from its definition -- that PA does not prove both A and ¬A for all sentences A of PA:
PA ⊢ ∀ A ( ¬Bew(ÍA ∧ ¬AÎ ) )
In all cases, regardless of how you express consistency of PA, the proof for the second incompleteness theorem always proceeds by considering the first incompleteness theorem:
PA ⊢ ∃ A ( A ⇔ ¬Bew(ÍAÎ ) )
The above means: There exists a sentence A that is (true and not provable) or (false and provable).
Say that G is such sentence:
PA ⊢ G ⇔ ¬Bew(ÍGÎ )
If PA can prove its consistency, then it can obviously also prove that G is consistent:
PA ⊢ ¬Bew(ÍG ∧ ¬GÎ )
By using the Hilbert-Bernays rewrite rules -- with a few more steps -- we can then prove that this expression leads to the following contradiction about G:
PA ⊢ ¬(G ⇔ ¬Bew(ÍGÎ ))
There are many ways to formulate the consistency of PA, i.e. Cons(PA), but proving it will always lead to a contradiction. Therefore, Cons(PA) is unprovable. According to the first incompleteness theorem, the following sentence is true:
Cons(PA) ∨ Incompl(PA)
So, PA is inconsistent or incomplete. However, we do not know if Cons(PA) is true. We can only come to that conclusion by proving it, but how are we supposed to do that? So, I disagree with the author when he writes:
It turns out that this statement is also true but unprovable.
This statement is only unprovable.
Of course, we can use Gentzen's equiconsistency proof with PRA but that does not prove PA's consistency. It just proves that it is equiconsistent with PRA (primitive recursive arithmetic). Who says that PRA is consistent? We don't know that. Other authors sometimes write that we can prove PA's consistency from within ZFC. Fine, but who says that ZFC is consistent?
Hence, we can only assume PA's consistency. We cannot just state Cons(PA) to be true. This cannot be done. -
 Tarskian
658Could you say a little more about what makes an unprovable mathematical proposition true? — Joshs
Tarskian
658Could you say a little more about what makes an unprovable mathematical proposition true? — Joshs
The fact that we can prove that it exists.
Let's start from Carnap's diagonal lemma. In the context of Peano arithmetic (PA), for each property φ(n) accepting one natural number n as input argument, there exists a true sentence S that does not have the property or a false sentence S that does have it:
PA ⊢ ∀ φ ∃ S ( S ⇔ ¬φ(ÍSÎ ) )
This is, in fact, the only hard part in Gödel's proof. The proof for the lemma is very short but it is widely considered to be incomprehensible:
https://proofwiki.org/wiki/Diagonal_Lemma
Say that Bew(ÍSÎ) is a property in PA that is true if it proves S and false when it doesn't. In that case, the lemma applies:
PA ⊢ ∀ φ ∃ S ( S ⇔ ¬Bew(ÍSÎ ) )
There exists a true sentence that is not provable or a false sentence that is provable. Hence, PA is incomplete or inconsistent. Let's denote this sentence as G:
PA ⊢ G ⇔ ¬Bew(ÍGÎ ) )
So, now we have a sentence that is (true or unprovable) or (false and provable). In fact, G is also a truly constructive witness for the theorem. But then again, we do not even need this particular sentence, because in the meanwhile, we also have Goodstein's theorem that is true but unprovable in PA:
https://en.wikipedia.org/wiki/Goodstein%27s_theorem
It is very hard to discover this kind of true but unprovable sentences. But then again, we also know that they massively outnumber the true and provable sentences. True but unprovable is the rule while true and provable is the exception. This is the paradoxical situation of the truth in PA. The truth in PA is highly chaotic but it is very hard for us to see that. -
 Tarskian
658Why should we suppose that natural languages are only countably infinite? — Banno
Tarskian
658Why should we suppose that natural languages are only countably infinite? — Banno
You can enumerate every sentence in natural language in a list. Therefore, it maps one to one onto the natural numbers. Therefore, their set is countable.
https://en.wikipedia.org/wiki/Countable_set
In mathematics, a set is countable if either it is finite or it can be made in one to one correspondence with the set of natural numbers.[a] Equivalently, a set is countable if there exists an injective function from it into the natural numbers; this means that each element in the set may be associated to a unique natural number, or that the elements of the set can be counted one at a time, although the counting may never finish due to an infinite number of elements.
For natural language to be uncountable, you must find a sentence that cannot be added to the list. To that effect, you would need some kind of second-order diagonal argument. -
 fishfry
3.4kThe world of mathematical truth does not look like most people believe it does. It is not orderly. It is fundamentally unpredictable. It is highly chaotic. — Tarskian
fishfry
3.4kThe world of mathematical truth does not look like most people believe it does. It is not orderly. It is fundamentally unpredictable. It is highly chaotic. — Tarskian
I didn't read the rest of this interesting thread yet so I'm just responding to the top post.
I believe Chaitin made a similar point. He has a proof of Gödel's incompleteness theorems from algorithmic complexity theory. I believe he says that mathematical truth is essentially random. Things are true just because they are, not because of any deeper reason.
This sounds related to what you're saying.
Why should we suppose that natural languages are only countably infinite? — Banno
The set of finite-length strings over an at most countably infinite alphabet is countable. There are countably many strings of length 1, countably many of length 2, dot dot dot, therefore countably many finite strings.
If you allow infinite strings, of course, you can have uncountably many strings. That's the difference between positive integers, which have finitely many digits; and real numbers, which have infinitely many. That's why the positive integers are countable and the real numbers uncountable. It's the infinitely long strings that make the difference. But natural language doesn't allow infinitely long strings. Every word or sentence is finite, so there can only be countably many of them.
a. Form the set of all subsets of S0, P(S0). — The Vastness of Natural Language
I didn't completely follow what you're doing, but in taking the powerset of a countably infinite set, you are creating an uncountable one. There aren't uncountably many words or phrases or strings possible in a natural language, if you agree that a natural language consists of a collection of finite-length strings made from at an most countably infinite alphabet. I think this might be a flaw in your argument, where you're introducing an uncountable set. -
 Tarskian
658I believe Chaitin made a similar point. He has a proof of Gödel's incompleteness theorems from algorithmic complexity theory. I believe he says that mathematical truth is essentially random. Things are true just because they are, not because of any deeper reason.
Tarskian
658I believe Chaitin made a similar point. He has a proof of Gödel's incompleteness theorems from algorithmic complexity theory. I believe he says that mathematical truth is essentially random. Things are true just because they are, not because of any deeper reason.
This sounds related to what you're saying. — fishfry
Yes, Yanofsky's paper also mentions Chaitin's work:
http://www.sci.brooklyn.cuny.edu/~noson/True%20but%20Unprovable.pdf
Gregory Chaitin described an innovative way of finding true but unprovable statements. He started by examining the complexity of the axioms of a logical system. He showed that there are certain statements that are much more complex than the axioms of the system. Such statements are true but cannot be proven by the axioms of the logical system. The following motto is sometimes used to explain this:
“A fifty-pound logical system cannot prove a seventy-five-pound theorem.”
In particular, basic arithmetic is a logical system that has a level of complexity and so there are certain types of statements that are true but too complex to be proven using basic arithmetic. The main point for our story is that within basic arithmetic we can always find more complicated statements of a certain type. Hence, there are infinitely many true but unprovable statements.
Cristian Calude extended Chaitin’s findings. He demonstrated that provable statements are actually very rare within the space of all true statements. In a sense, he showed that in the space of all true statements, every provable true statement is surrounded by many unprovable true statements.
This means that most (but not all) mathematical truth is essentially random.
Yanofsky's paper mentions an even larger class of random mathematical truth: unprovable because ineffable ("inexpressable"). There is no way to prove truths that cannot even be expressed in language. Because in that case, how are you going to express the proof? That class of random truths is even larger than Chaitin's random truths.
But then again, there exists a small class of true and provable statements.
In fact, nature of mathematical facts is quite similar to the nature of facts in the physical universe. Mostly random but with a relatively small class of facts that is still predictable. Unlike what most people believe, math is not more orderly than the physical universe itself. -
 Wayfarer
26.2kUnlike what most people believe, math is not more orderly than the physical universe itself. — Tarskian
Wayfarer
26.2kUnlike what most people believe, math is not more orderly than the physical universe itself. — Tarskian
Nevertheless, and to all practical purposes, mathematics enables a very wide range of successful predictions, doesn’t it? The mathematical physics underlying the technology on which this conversation is being conducted provides a high degree of prediction and control, doesn’t it? Otherwise, it wouldn’t work. -
 fishfry
3.4kYes, Yanofsky's paper also mentions Chaitin's work: — Tarskian
fishfry
3.4kYes, Yanofsky's paper also mentions Chaitin's work: — Tarskian
Thanks, I'll check out that paper.
Yanofsky's paper mentions an even larger class of random mathematical truth: unprovable because ineffable ("inexpressable"). There is no way to prove truths that cannot even be expressed in language. — Tarskian
True yet inexpressible in language. Great concept. -
 Philosophim
3.6kThe world of mathematical truth does not look like most people believe it does. It is not orderly. It is fundamentally unpredictable. It is highly chaotic. — Tarskian
Philosophim
3.6kThe world of mathematical truth does not look like most people believe it does. It is not orderly. It is fundamentally unpredictable. It is highly chaotic. — Tarskian
This is a far cry from the point that math can be difficult to put into words. The proof is in the very fact you're able to post online consistently for us to read your posts. That was all capable through math. -
 Tarskian
658Nevertheless, and to all practical purposes, mathematics enables a very wide range of successful predictions, doesn’t it? The mathematical physics underlying the technology on which this conversation is being conducted provides a high degree of prediction and control, doesn’t it? Otherwise, it wouldn’t work. — Wayfarer
Tarskian
658Nevertheless, and to all practical purposes, mathematics enables a very wide range of successful predictions, doesn’t it? The mathematical physics underlying the technology on which this conversation is being conducted provides a high degree of prediction and control, doesn’t it? Otherwise, it wouldn’t work. — Wayfarer
There are two directions.
If it is provable, then it is always true. (aka, soundness theorem) In this direction, everything is very orderly. That is the only direction that we really use. That is why works so well.
If it is true, then it is almost surely not provable. In this direction, everything is very chaotic. We almost never use this direction. In fact, we cannot even see most of these random truths. So, why would we try to prove them?
It took Gödel all kinds of acrobatics in metamathematics to discover that these unpredictable truths even exist.
Before the publication of Gödel's paper in 1931, nobody even knew about these random truths. Most mathematicians were actually convinced that if it is true, then it is surely provable. Pretty much everybody on the planet was wrong about this before 1931. They were all deeply steeped in positivism. David Hilbert even asked for a formal proof of this glaring error. In fact, there are still a lot of people who believe this. Almost a century after its refutation, it is still a widespread misconception. -
 Tarskian
658This is a far cry from the point that math can be difficult to put into words. The proof is in the very fact you're able to post online consistently for us to read your posts. That was all capable through math. — Philosophim
Tarskian
658This is a far cry from the point that math can be difficult to put into words. The proof is in the very fact you're able to post online consistently for us to read your posts. That was all capable through math. — Philosophim
All of this is the result of using just one direction ("soundness"):
If it is provable, then it is always true.
That is the only direction that we use in engineering. We never use the other direction:
If it is true, then it is pretty much never provable. It is a rare exception, if it is.
In math, we mostly don't even see these unpredictable truths. How would we? In the physical universe, we can definitely see the unpredictable chaos, but we mostly ignore it. Mathematical truth is as chaotic as the truth in the physical universe. In my opinion, there is not much difference. We typically just don't want to know about it. -
 ssu
9.8k
ssu
9.8k
Perhaps some can see this as chaotic, but math itself is quite logical and hence quite orderly. Unprovability or uncomputability doesn't mean chaotic. Math is orderly, we just have limitations on what to compute or prove.The world of mathematical truth does not look like most people believe it does. It is not orderly. It is fundamentally unpredictable. It is highly chaotic. — Tarskian
Of course it matters just how we define Chaos. If it's logical, it surely can be also mathematical.
The fact that people have a difficult time is to grasp that mathematics can be uncomputable (and unprovable). Non-computable mathematics sounds like an oxymoron, right? Wrong, only part of mathematics is computable. Or countable or provable.
Let's take a simple example just how easily we can get true, but not known mathematical entity. Assume a, b and c are distinct numbers that belong to the Natural numbers.
Let's have the equation
a + b = c
if we know two of them, we know the third one. So if a is 2 and b is 3, then c has to be 5. The equation, which is a bijective function, is obvious and easy.
It isn't so obvious when we have an inequation, which isn't a bijection:
a + b < c
If a is 2 and b is 3, then c has to be something bigger than 5 and when c belonged to the natural numbers, it's then 6 or larger. And that's it! Even if it obviously c is a natural number and has a precise point on the number line, not some range, we cannot prove c exactly. The only equation or bijection that we can do is that c=c (and c is 6 or a higher natural number).
The problem rises because we just assume that everything in math has to be provable. And the real culprit here is that when mathematics has risen from the need to count, we have put counting/computing as the basis of all math. That is an error, because we have non-computable math, and hence if we want mathematics to be consistent and logical, somethings got to give. -
 Tarskian
658Perhaps some can see this as chaotic, but math itself is quite logical and hence quite orderly. Unprovability or uncomputability doesn't mean chaotic. Math is orderly, we just have limitations on what to compute or prove. — ssu
Tarskian
658Perhaps some can see this as chaotic, but math itself is quite logical and hence quite orderly. Unprovability or uncomputability doesn't mean chaotic. Math is orderly, we just have limitations on what to compute or prove. — ssu
I started using unpredictability as somewhat a synonym for unprovability because of how Stephen Hawking put it:
https://www.hawking.org.uk/in-words/lectures/godel-and-the-end-of-physics
What is the relation between Godel’s theorem and whether we can formulate the theory of the universe in terms of a finite number of principles? One connection is obvious. According to the positivist philosophy of science, a physical theory is a mathematical model. So if there are mathematical results that can not be proved, there are physical problems that can not be predicted.
So, we are sitting on a system that is largely unpredictable because most of its truths are unprovable. A system that is largely unpredictable is deemed chaotic:
Chaos theory is an interdisciplinary area of scientific study and branch of mathematics. It focuses on underlying patterns and deterministic laws of dynamical systems that are highly sensitive to initial conditions. These were once thought to have completely random states of disorder and irregularities.[1] Chaos theory states that within the apparent randomness of chaotic complex systems, there are underlying patterns, interconnection, constant feedback loops, repetition, self-similarity, fractals and self-organization.[2]
This can happen even though these systems are deterministic, meaning that their future behavior follows a unique evolution[8] and is fully determined by their initial conditions, with no random elements involved.[9] In other words, the deterministic nature of these systems does not make them predictable.[10][11] This behavior is known as deterministic chaos, or simply chaos.
The only minor difference between the universe of arithmetical truth and a chaotic system is that there are no "initial conditions" that we can change in order to produce a completely different version of arithmetical truth.
Even if it obviously c is a natural number and has a precise point on the number line, not some range, we cannot prove c exactly. — ssu
Imagine that we somehow have the information that c=17. Without additional information, it is not possible to prove it. In that sense, c is true but not provable. It could even be impossible to prove. In the standard model of arithmetic, i.e. in the natural numbers, we can somehow see that c=17 but in various nonstandard models, we can see that c is not 17. In those circumstances, proof is not even possible. Only when c=17 in all models of arithmetic, a proof is possible.
The problem rises because we just assume that everything in math has to be provable. — ssu
Yes, David Hilbert even wanted proof for that. In his view, every true statement must have a proof:
https://en.wikipedia.org/wiki/Hilbert%27s_program
Statement of Hilbert's program
- A formulation of all mathematics; in other words all mathematical statements should be written in a precise formal language, and manipulated according to well defined rules.
- Completeness: a proof that all true mathematical statements can be proved in the formalism.
- Consistency: a proof that no contradiction can be obtained in the formalism of mathematics. This consistency proof should preferably use only "finitistic" reasoning about finite mathematical objects.
- Conservation: a proof that any result about "real objects" obtained using reasoning about "ideal objects" (such as uncountable sets) can be proved without using ideal objects.
- Decidability: there should be an algorithm for deciding the truth or falsity of any mathematical statement.
Hilbert believed it so strongly that he insisted that all his colleagues should work on proving the above. A lot of people still believe it. You can give them proof that it is absolutely impossible, but they simply don't care about that. They will just keep going as if nothing happened. You can't wake a person who is pretending to be asleep. -
 ssu
9.8k
ssu
9.8k
The basic problem is that people simply have these ideas what mathematics should be like and don't notice that their own premises, which they hold as axioms (obviously! What else they could they be?), aren't actually true. And when those "axioms" aren't true, we end up somewhere in a paradox.Hilbert believed it so strongly that he insisted that all his colleagues should work on proving the above. A lot of people still believe it. You can give them proof that it is absolutely impossible, but they simply don't care about that. They will just keep going as if nothing happened. You can't wake a person who is pretending to be asleep. — Tarskian
Easiest misunderstanding to understand was the idea of all numbers being rational. Why? Because math had to be perfect! And then when obviously there were irrational numbers, the story goes that the man, Hippasus, who found irrational numbers was ostracized and when he drowned at sea, it was the "punishment of the Gods". So that at least show how some Greeks thought about it. Yet since some irrational numbers were so useful, irrational numbers were accepted.
Then there's the mess that Russell found out and the collective panic attack that only subsided with ZF-logic simply banning the paradox. There's obviously still a lot of confusion. But we can look at this in a very positive light: there's a lot for us to discover still! -
 ssu
9.8kI agree
ssu
9.8kI agree
Gödel didn't make it easy. In my opinion Cantor's diagonalization is an easier model. Or basically just use negative self reference with avoiding a Cretan liar situation.This is, in fact, the only hard part in Gödel's proof. The proof for the lemma is very short but it is widely considered to be incomprehensible: — Tarskian
What I don't get is just how little interest the diagonalization (or negative self-reference) gets. Yet with using it Cantor showed that the reals cannot be put into a one-to-one correspondence with the natural numbers. And Turing used it in the Halting Problem and Gödel in the incompleteness Theorems. And here's the key: if we disregard this, we end up in a paradox.
For example, I can write (if I do write it correctly) the following self-referential statement, which is true:
"I can write anything what I write" meaning, that I have no limitations on what I write and what I write is then defined to be something that I wrote or, my writings.
Then let's turn into a negative self-reference, which is also true: "I cannot write anything what I don't write". OMG! Can I write anything? Obviously I can. Does this somehow limit what I can write? No, but it shows that obviously there also is something that I don't write, these writings exist.
Now here's the tricky part: If I make the false assumption that "I can write anything" means that there cannot be anything that I cannot write (if we skip the physical limitations and stick to the theoretical) what would that imply?,
I would have to write also what I don't write, which cannot be.
So in a way, negative self reference in my opinion is a very essential building block for logic. And everytime when someone makes an universal statement that ought to apply to everything, watch out! -
 Tarskian
658I think you’re mis-using the word there. If everything were chaotic, nothing would exist, and if everything were perfectly ordered, nothing would change. Existence requires both. Beyond that, I can’t see the point, if there is one. — Wayfarer
Tarskian
658I think you’re mis-using the word there. If everything were chaotic, nothing would exist, and if everything were perfectly ordered, nothing would change. Existence requires both. Beyond that, I can’t see the point, if there is one. — Wayfarer
People seem to understand this about the truth in the physical universe. They tend to reject this about the truth in arithmetic. I wanted to point out that the situation is the same. -
 Tarskian
658And everytime when someone makes an universal statement that ought to apply to everything, watch out! — ssu
Tarskian
658And everytime when someone makes an universal statement that ought to apply to everything, watch out! — ssu
That may very well be in violation of Carnap's diagonal lemma:
"For each property of logic sentences, there exists a true sentence that does not have it, or a false sentence that does."
But then again, it still needs to be a property of logic sentences. For example, a property of natural numbers can apply to all natural numbers. -
 RussellA
2.7kSo in a way, negative self reference in my opinion is a very essential building block for logic. — ssu
RussellA
2.7kSo in a way, negative self reference in my opinion is a very essential building block for logic. — ssu
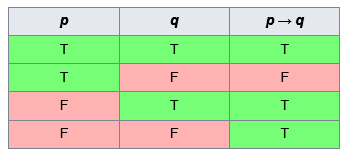
Let p be "I can write anything". Let q be "I know everything".
Consider the statement "If I can write anything then I know everything"
"If I can write anything then I know everything" seems reasonably true.
"If I can write anything then I don't know everything" seems reasonably false.
"If I cannot write anything then I don't know everything" seems reasonable true'.
However, as regards logic using the Truth Tables, "if I cannot write anything then I know everything" is true, regardless of whether it initially seems unreasonable.
In logic, negative expressions are as important as positive expressions, but can lead to strange places. -
 Treatid
54The set of finite-length strings over an at most countably infinite alphabet is countable. There are countably many strings of length 1, countably many of length 2, dot dot dot, therefore countably many finite strings. — fishfry
Treatid
54The set of finite-length strings over an at most countably infinite alphabet is countable. There are countably many strings of length 1, countably many of length 2, dot dot dot, therefore countably many finite strings. — fishfry
But a sentence is not the same as a string.
The interpretation of a sentence depends on the context/axioms. The same string in two axiomatic systems is two distinct sentences.
In regard to the paper you referenced in the OP this can probably be fixed up to reference only the possible statements in a single axiomatic system. However, the assertion that natural languages are countably infinite no longer holds given there are an uncountable infinite number of contexts for any given sentence.
Way out there take
I would go significantly further.
The interpretation of statements within an axiomatic system are determined by the context/axioms.
In order to consistently and correctly interpret a given statement within an axiomatic system it is necessary to have an accurate and complete statement of context.
That is, the axioms for an axiomatic system must, themselves, have a complete statement of context (axioms must have axioms to determine how those axioms should be interpreted).
This results in infinite regression.
Axiomatic Mathematics/mathematicians do try to mitigate this problem by using previous axiomatic systems to specify axioms for subsequent axiomatic systems; but this only obfuscates the problem, it doesn't resolve the fundamentally unresolveable issue:
Without a full and complete initial specification of context, it is impossible to derive a full and complete specification of context. -
 ssu
9.8kEspecially to my statements, yes! But that's why you are here, to correct if there's something wrong or is mistaken. :wink:
ssu
9.8kEspecially to my statements, yes! But that's why you are here, to correct if there's something wrong or is mistaken. :wink: -
 Philosophim
3.6kThat is the only direction that we use in engineering. We never use the other direction:
Philosophim
3.6kThat is the only direction that we use in engineering. We never use the other direction:
If it is true, then it is pretty much never provable. It is a rare exception, if it is. — Tarskian
Ah, it depends on how you're using the word 'truth'. If you mean absolutely truth or, "what is," yeah, its hard to find those. If you're talking about propositional logic or terms in math, then true/false is fine. I just think you're being a bit dramatic. :)
Knowledge is a tool. Because its not precise to the nano-meter, does that mean a wrench is highly chaotic and unpredictable? Of course not. Our language, while imprecise at times, is useful for its imprecision for efficiency. Just like I wouldn't grab a wrench if I were studying the atomic level of the universe, one shouldn't use certain language and terms when dealing with the foundations of knowledge and mathematics.
The hyperbole just isn't true. Its like standing in a white room and noting, "Look how chaotic the colors are, flying every which way around this room! The chaos!" And of course there's someone looking at you from the outside wondering if they should pad the walls and give you a jacket to go with it. -
 Tarskian
658Just like I wouldn't grab a wrench if I were studying the atomic level of the universe, one shouldn't use certain language and terms when dealing with the foundations of knowledge and mathematics. — Philosophim
Tarskian
658Just like I wouldn't grab a wrench if I were studying the atomic level of the universe, one shouldn't use certain language and terms when dealing with the foundations of knowledge and mathematics. — Philosophim
The true nature of the universe of mathematical facts makes lots of people uncomfortable.
Imagine that we had a copy of the theory of everything?
It would allow us to mathematically prove things about the physical universe. It would be the best possible knowledge that we could have about the physical universe. We would finally have found the holy grail of science.
What would the impact be?
Well, instead of being able to predict just 0.1% of the facts in the physical universe, this would improve to something like 0.3%; and not much more.
Scientism is widespread as an ideology in the modern world. Any true understanding of the nature of mathematical truth deals a devastating blow to people who subscribe to it. This is exactly why I like this subject so much.
The hyperbole just isn't true. — Philosophim
That is wishful thinking.
You may not want it to be true, but it is.
In 1931, Gödel's incompleteness theorems dealt a major blow to positivism and scientism, but it was just the beginning. It is only going to keep getting worse. As Yanovsky writes in his paper:
Gödel’s famous incompleteness theorem showed us that there is a statement in basic arithmetic that is true but can never be proven with basic arithmetic. That is just the beginning of the story.
In my opinion, scientism needs to get attacked and destroyed because its narrative is not just arrogant but fundamentally evil. It is a dangerously false pagan belief that misleads its followers into accepting untested experimental vaccine shots from the lying and scamming representatives of the pharmaceutical mafia; and that is just one of the many examples of why all of this is not hyperbole. -
 Pantagruel
3.6kdangerously false pagan belief that misleads its followers into accepting untested experimental vaccine shots from the lying and scamming representatives of the pharmaceutical mafia — Tarskian
Pantagruel
3.6kdangerously false pagan belief that misleads its followers into accepting untested experimental vaccine shots from the lying and scamming representatives of the pharmaceutical mafia — Tarskian
It sounds as though you yourself hold some rather specific and rigid beliefs that likewise are not entirely objective in their genesis.
Welcome to The Philosophy Forum!
Get involved in philosophical discussions about knowledge, truth, language, consciousness, science, politics, religion, logic and mathematics, art, history, and lots more. No ads, no clutter, and very little agreement — just fascinating conversations.
Categories
- Guest category
- Phil. Writing Challenge - June 2025
- The Lounge
- General Philosophy
- Metaphysics & Epistemology
- Philosophy of Mind
- Ethics
- Political Philosophy
- Philosophy of Art
- Logic & Philosophy of Mathematics
- Philosophy of Religion
- Philosophy of Science
- Philosophy of Language
- Interesting Stuff
- Politics and Current Affairs
- Humanities and Social Sciences
- Science and Technology
- Non-English Discussion
- German Discussion
- Spanish Discussion
- Learning Centre
- Resources
- Books and Papers
- Reading groups
- Questions
- Guest Speakers
- David Pearce
- Massimo Pigliucci
- Debates
- Debate Proposals
- Debate Discussion
- Feedback
- Article submissions
- About TPF
- Help
More Discussions
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum












