-
 Gregory
5kThe difference between an arithematic infinity and a spacial/geometric one is that in the former the numbers have no spatial size and can thus sum to a finite sum. In the latter there are infinite instantiated steps, hence Zeno.
Gregory
5kThe difference between an arithematic infinity and a spacial/geometric one is that in the former the numbers have no spatial size and can thus sum to a finite sum. In the latter there are infinite instantiated steps, hence Zeno.
Most people seem to think Zeno was a minor philosopher. He was actually the first in the West to write a book of philosophy as that is understood in the modern sense. No one before him asked questions about the infinite like that. He was a Newton of his time. To think of infinite division back then was incredible. We still debate this today -
 fishfry
3.4kThanks. So you simply extend the natural number to the extended natural number and resolve the problem of indexing. — MoK
fishfry
3.4kThanks. So you simply extend the natural number to the extended natural number and resolve the problem of indexing. — MoK
Yes exactly.
The difference between an arithematic infinity and a spacial/geometric one is that in the former the numbers have no spatial size and can thus sum to a finite sum. In the latter there are infinite instantiated steps, hence Zeno. — Gregory
The geometric idea is exactly the same.
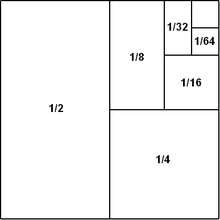
Consider the half-open unit interval [0,1) which includes 0 and excludes 1. It has length 1. Now break it up into an infinite union of many subintervals:
[0,1/2) [1/2, 3/4) [3/4, 7/8) [7/8, 15/16) ...
That's a geometric decomposition of an interval of length 1 into pairwise disjoint subintervals of lengths 1/2, 1/4, 1/8, ... respectively, representing the arithmetic infinite sum 1/2 + 1/4 + 1/8 + ... = 1.
You can toss in the right endpoint of 1, which, being a point, has length 0 and makes no difference to the length.
Wikipedia has a 2-dimensional version of this visual proof.
-
 TonesInDeepFreeze
3.8k
TonesInDeepFreeze
3.8k
Not "extended natural number".
Rather the ordinal w+1 = wu{w}. That has been explained to you probably at least five times already.
And there is no "problem of indexing". You're using the word 'indexing' incorrectly, as I've explained to you twice already.
Any set can be indexed by being the range of a function. Indeed, trivially, any set is indexed by being the range of the identity function on the set.
Your question might be whether a certain set can be indexed by w. By definition, any denumerable set can be indexed by w.
But your question might go further: Can a set with an ordering on the set be isomorphic with w and the usual ordering on w. Of course, there are sets and orderings that are not isomorphic with one another. For example, in the current discussion, consider a set ordered
1 2 3 ...
That is isomorphic with the standard ordering on w.
Consider a set ordered
1 2 3 ... x
That is not isomorphic with the standard ordering on w
But it is isomorphic with the standard ordering on w+1.
But these explanations are wasted on you because you won't actually look at a beginning reference on this subject so that your claims and questions aren't based on your confusions and ignorance. -
 TonesInDeepFreeze
3.8kThanks. So you simply extend the natural number to the extended natural number and resolve the problem of indexing.
TonesInDeepFreeze
3.8kThanks. So you simply extend the natural number to the extended natural number and resolve the problem of indexing.
— MoK
Yes exactly. — fishfry
Except that w is not called an "extended natural number". -
 fishfry
3.4kNot "extended natural number". — TonesInDeepFreeze
fishfry
3.4kNot "extended natural number". — TonesInDeepFreeze
I have no problem with that terminology which avoids getting into ordinals, which people find confusing. I learned that in the other thread. -
 fishfry
3.4kI wouldn't, but suit yourself. — TonesInDeepFreeze
fishfry
3.4kI wouldn't, but suit yourself. — TonesInDeepFreeze
If you believe in the extended reals, just setminus all the finite non-integers and you're left with the integers along with the two points at infinity. Why on earth can't you call that the extended integers; or taking the nonnegative ones, the extended naturals? It's perfectly ... natural. -
 TonesInDeepFreeze
3.8kWrong. I explained the difference between them. Knowing the definition of 'the continuum' does not provide knowing the definition of 'continuous'.
TonesInDeepFreeze
3.8kWrong. I explained the difference between them. Knowing the definition of 'the continuum' does not provide knowing the definition of 'continuous'.
— TonesInDeepFreeze
Do you mind elaborating? — MoK
What's to elaborate? I gave you the definitions of 'the continuum' and 'continuous function'. Meanwhile, a definition of 'a continuum' is not needed in this context, only 'the continuum'. Moreover there are different definitions of 'a continuum' in different contexts and they are way too technical for you. For purposes of the discussion at this juncture, 'the continuum' is sufficient. You ask for elaboration on concepts that depend on previous concepts that you refuse to learn. You won't even find out for yourself what a function is but you want people to explain mathematics to you. -
 TonesInDeepFreeze
3.8k
TonesInDeepFreeze
3.8k
You can call them whatever you want.
(I see that there is a Wikipedia article that does use the terminology though. I don't usually reference the unreliable and haphazardly edited Wikipedia for mathematics.)
But sequences are defined as having ordinals as the domain. That clarifies and can be widely referenced in the literature. And the extended reals of course is also a common notion. But the points of infinity in the extended reals are not ordinarily (if at all) understood as ordinals that are the domains of sequences. -
 fishfry
3.4kYou can call them whatever you want. — TonesInDeepFreeze
fishfry
3.4kYou can call them whatever you want. — TonesInDeepFreeze
Consider the following set
with the order
for
Why do you refuse to call that the extended integers, and the subset of nonnegatives the extended naturals; and to write (so far) two posts objecting to this simple and natural terminology?
See this SE discussion. The consensus seemed to be that they're not generally useful; not that the terminology, which is perfectly obvous, is wrong.
https://math.stackexchange.com/questions/1442961/extended-integers -
 TonesInDeepFreeze
3.8k
TonesInDeepFreeze
3.8k
It's not a quirk. It's odd terminology, as far as I know; and the context here is not just points at infinity but sequences, and sequences are functions whose domain is an ordinal (or at least a set with a well ordering).
The standard ordering on the real numbers is not a well ordering. So talking about points of infinity as in the domain of a sequence is confusing at best.
The sequence is (I'm taking the liberty of starting at 1 rather than at 0):
{<1 step-1> <2 step-2> ... <w final-state>} -
 fishfry
3.4kThe standard ordering on the real numbers is not a well ordering. So talking about points of infinity as in the domain of a sequence is confusing at best. — TonesInDeepFreeze
fishfry
3.4kThe standard ordering on the real numbers is not a well ordering. So talking about points of infinity as in the domain of a sequence is confusing at best. — TonesInDeepFreeze
It's a pedagogical point. It's far far easier for people to understand the point at infinity as the index of the limit of a sequence, than to explain the ordinal ; even if the latter is more mathematically precise. But in this context it makes no difference whatsoever.
I learned this at length in the supertask thread. The idea is to communicate and educate, not to stand on pointless pedantry at the risk of confusing people. Try to consider this point.
In fact if it makes you happy, I'll just tell you that is my own personal notation for what everyone else calls , and now you have no possible objection.
I won't be further responding to this silly and trivial subtopic, but lest anyone think I'm thereby conceding the point, I'm not. Your obsessive pedantry is leading you astry. From now on when I say, "extended natural numbers" just remember that this is my pet name for and all will be well. -
 TonesInDeepFreeze
3.8kYou mean the ordering:
TonesInDeepFreeze
3.8kYou mean the ordering:
L u {<-inf n> | n in w} u {<n inf}> | n in w}, where L is the standard ordering on the natural numbers.
The formulation you gave doesn't mention that the ordering includes the standard ordering on w; it only mentions that every member of w is greater than -inf and less than inf. -
 TonesInDeepFreeze
3.8k
TonesInDeepFreeze
3.8k
It's not pedantic but it is pedagogical.
The key idea is sequences. And it is clear and concise to say:
The domain is w+1 = wu{w} (or, taking liberties (w\{0})u{w}).
But to go through cutting the real numbers down to positive integers and then adding points of infinity (moreover raising the pedagogical question of what exactly are "points of infinity") is an unnecessary detour and distracts from the insight of using sequences. Indeed, such things as dividing infinitely in a discussion such as this involves explicitly sequences. So the insight is that we have sequences not just on the ordinal w but also on ordinals such as w+1. Indeed that highlights that the range of such sequences may have other than ordinals (such as natural numbers) but that the domains are ordinals.
You may use the lemniscate however you wish. But I wouldn't use it for w. Because it is a typical that uninformed people (I mean other posters, not you) are prone to use "infinity" as a catch-all for infinite sets. Indeed a point of infinity in the extended reals may be any set whatsoever except a real; doesn't even have to be an infinite set. That is, if we want to instantiate the extended real system, then we only need to choose two sets that are not themselves real numbers, then define the ordering and operations in the usual manner.
But uninformed people don't distinguish between inf ('inf' read as the lemniscate) and the set of natural numbers. They regularly conflate inf ("infinity") with the set of natural numbers, which is an infinite set but not necessarily a point of infinity in the extended reals. So it is good pedagogically to use notation that doesn't lead to that conflation.
On the other hand, making an analogy between w+1 and the positive extended reals is a nice idea. I would state it as only an analogy though.
But of course, you are free to stipulate whatever definitions you like. -
 fishfry
3.4kThe formulation you gave doesn't mention that the ordering includes the standard ordering on w; it only mentions that every member of w is greater than -inf and less than inf. — TonesInDeepFreeze
fishfry
3.4kThe formulation you gave doesn't mention that the ordering includes the standard ordering on w; it only mentions that every member of w is greater than -inf and less than inf. — TonesInDeepFreeze
LOL. Pedants 'Я' us. -
 TonesInDeepFreeze
3.8k
TonesInDeepFreeze
3.8k
[emphasis added]Your obsessive pedantry is leading you astry. — fishfry
Your penchant for making discussions personal leads you astray. -
 fishfry
3.4kYour penchant for making discussions personal leads you astray. — TonesInDeepFreeze
fishfry
3.4kYour penchant for making discussions personal leads you astray. — TonesInDeepFreeze
I've been watching you insult the OP for days now. Project much? -
 TonesInDeepFreeze
3.8kThe formulation you gave doesn't mention that the ordering includes the standard ordering on w; it only mentions that every member of w is greater than -inf and less than inf.
TonesInDeepFreeze
3.8kThe formulation you gave doesn't mention that the ordering includes the standard ordering on w; it only mentions that every member of w is greater than -inf and less than inf.
— TonesInDeepFreeze
LOL. Pedants 'Я' us. — fishfry
That is not pedantic. The formuation you gave is literally very incorrect. I simply offered a correct formulation. For that, you reply petulantly (though not pedantically). Maybe, eventually, you'll get past nonsense like that. -
 TonesInDeepFreeze
3.8k
TonesInDeepFreeze
3.8k
After many posts where I made no personal comments, I have correctly said that the poster is ignorant and confused about mathematics. And that is not gratuitous, especially as he persists to ignore the information and explanations given him. That is not analogous to your nearly immediately taking umbrage at corrections or suggestions for sharper formulation and then turning that to one of your sophomoric snipes. And, in this case, instead of responding to my substantive points about the terminology. -
 MoK
1.9k
MoK
1.9k
It is alright guys. I learned lots of things from both of you and I am thankful for it. I don't think that personal attacks are useful though when people can discuss things openly, so one party learns and another party teaches. I have to say that the process of learning is time and energy consuming so it is alright if one person needs the explanation of things a few times. -
 TonesInDeepFreeze
3.8k
TonesInDeepFreeze
3.8k
Bull. You spout misinformation. Then you get explanations and ignore them, evidenced by asking questions that were already answered as you just go right ahead to re-spout. And you refuse to grasp the very simple fact that any explanation given you relies on previous concepts so that both the logical way and only downright practical way to know any of this is for you to start at page 1. If not trolling literally, it is trolling de facto. But do carry on ... it is amusing as pathetic comedy. -
 jgill
4kIf only the standard analysis of the reals had been discussed, with infinity not a member and infinitesimals not (re)introduced, perhaps things would have terminated long ago. Maybe not, but I would guess most physicists don't dabble in non-standard analysis nor are they concerned with the roles of ultrafilters in pointless topology. I could be wrong but even introducing ordinals into the discussion opens a Pandoras Box. Just my opinion.
jgill
4kIf only the standard analysis of the reals had been discussed, with infinity not a member and infinitesimals not (re)introduced, perhaps things would have terminated long ago. Maybe not, but I would guess most physicists don't dabble in non-standard analysis nor are they concerned with the roles of ultrafilters in pointless topology. I could be wrong but even introducing ordinals into the discussion opens a Pandoras Box. Just my opinion. -
 fishfry
3.4kIf only the standard analysis of the reals had been discussed, with infinity not a member and infinitesimals not (re)introduced, perhaps things would have terminated long ago. Maybe not, but I would guess most physicists don't dabble in non-standard analysis nor are they concerned with the roles of ultrafilters in pointless topology. I could be wrong but even introducing ordinals into the discussion opens a Pandoras Box. Just my opinion. — jgill
fishfry
3.4kIf only the standard analysis of the reals had been discussed, with infinity not a member and infinitesimals not (re)introduced, perhaps things would have terminated long ago. Maybe not, but I would guess most physicists don't dabble in non-standard analysis nor are they concerned with the roles of ultrafilters in pointless topology. I could be wrong but even introducing ordinals into the discussion opens a Pandoras Box. Just my opinion. — jgill
As a complex analysis guy you use the hypothetical point at infinity of the Riemann sphere all the time, don't you? It's just the one-point compactification of the plane. The circle is the one-point compactification of the real line, and the extended reals are the two-point compactification. -
 jgill
4kAs a complex analysis guy you use the hypothetical point at infinity of the Riemann sphere all the time, don't you? — fishfry
jgill
4kAs a complex analysis guy you use the hypothetical point at infinity of the Riemann sphere all the time, don't you? — fishfry
Only on rare occasion. Normally, Infinity for me means unbounded. I don't work on the Riemann sphere. Yes, projective stuff is there in the background, like circles with infinite radius are lines, etc. But I am very old fashioned. Here is the sort of thing that has interested me. -
 Metaphysician Undercover
14.7kave correctly said that the poster is ignorant and confused about mathematics. — TonesInDeepFreeze
Metaphysician Undercover
14.7kave correctly said that the poster is ignorant and confused about mathematics. — TonesInDeepFreeze
MO of the supreme sophist, Tones in the Deep Freeze. -
 TonesInDeepFreeze
3.8kave correctly said that the poster is ignorant and confused about mathematics.
TonesInDeepFreeze
3.8kave correctly said that the poster is ignorant and confused about mathematics.
— TonesInDeepFreeze — Metaphysician Undercover
The quintessential crank* Metaphysician Undercover misquotes me. I didn't post any sentence that begins with "ave". But this is a true sentence I did post:
After many posts where I made no personal comments, I have correctly said that the poster is ignorant and confused about mathematics. — TonesInDeepFreeze
If I have an "MO" it is providing an ignorant and confused poster with information and explanations (the poster himself this time makes a point of repeatedly saying that the information and explanations have been helpful to him) but also remarking on the emerging pertinent point that the poster persists in ignorance and confusion.
But now the crank, himself ignorant and confused about mathematics, emerges with a false, pointless, substanceless, sophomoric, clueless attempt at wit, including even botching his quote of me. He has nothing to say other than to spit an inane, gratuitous attempt at a snipe. Actually, it's good that he doesn't say anything about the subject of discussion, since virtually everything he spouts about mathematics is irrational disinformation.
* Being a crank includes sophistry and more. -
 TonesInDeepFreeze
3.8k
TonesInDeepFreeze
3.8k
Back to matters at hand:
Hopefully you might now at least be beginning to understand the answers to your question:
There is the denumerable sequence that pairs each step in the staircase with a natural number. But there is also a proper superset of that sequence that has the set of natural numbers (w) itself as an argument and you may define whatever you wish to be the value of the sequence at that argument.
For example (starting with 1 instead of 0):
1 maps to 1
2 maps to 1/2
3 maps to 1/4
...
w maps to 0
I take from @fishfry (as an analogy in my thinking) that the extended reals have a point of positive infinity (inf) that is like w in this sense: inf is not itself an integer, but it is an extension that comes after all the integers. And w is not itself a natural number, but it is an ordinal that comes after all the natural numbers. -
 fishfry
3.4kI take from fishfry (as an analogy in my thinking) that the extended reals have a point of positive infinity (inf) that is like w in this sense: inf is not itself an integer, but it is an extension that comes after all the integers. And w is not itself a natural number, but it is an ordinal that comes after all the natural numbers. — TonesInDeepFreeze
fishfry
3.4kI take from fishfry (as an analogy in my thinking) that the extended reals have a point of positive infinity (inf) that is like w in this sense: inf is not itself an integer, but it is an extension that comes after all the integers. And w is not itself a natural number, but it is an ordinal that comes after all the natural numbers. — TonesInDeepFreeze
Yes.
https://en.wikipedia.org/wiki/Extended_real_number_line
The extended reals are used so that we can write things like and . They're essentially a notational convenience in calculus and real analysis.
I learned from experience in the supertask thread that it's easier to explain indexing the limit of a sequence as a point at infinity, rather than introducing the concept of the ordinal .
Only on rare occasion. Normally, Infinity for me means unbounded. I don't work on the Riemann sphere. Yes, projective stuff is there in the background, like circles with infinite radius are lines, etc. But I am very old fashioned. Here is the sort of thing that has interested me. — jgill
Thanks for that interesting link. I seem to remember you talking about this a while back.
My point was just that you've seen hypothetical points at infinity, they are nothing new or strange. They come up in many difference contexts.
Welcome to The Philosophy Forum!
Get involved in philosophical discussions about knowledge, truth, language, consciousness, science, politics, religion, logic and mathematics, art, history, and lots more. No ads, no clutter, and very little agreement — just fascinating conversations.
Categories
- Guest category
- Phil. Writing Challenge - June 2025
- The Lounge
- General Philosophy
- Metaphysics & Epistemology
- Philosophy of Mind
- Ethics
- Political Philosophy
- Philosophy of Art
- Logic & Philosophy of Mathematics
- Philosophy of Religion
- Philosophy of Science
- Philosophy of Language
- Interesting Stuff
- Politics and Current Affairs
- Humanities and Social Sciences
- Science and Technology
- Non-English Discussion
- German Discussion
- Spanish Discussion
- Learning Centre
- Resources
- Books and Papers
- Reading groups
- Questions
- Guest Speakers
- David Pearce
- Massimo Pigliucci
- Debates
- Debate Proposals
- Debate Discussion
- Feedback
- Article submissions
- About TPF
- Help
More Discussions
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum






