-
 jgill
4kBut patterns are nothing more than what humans perceive is beautiful, — Gregory
jgill
4kBut patterns are nothing more than what humans perceive is beautiful, — Gregory
There are patterns that are not beautiful. For instance, an aerial view of a battlefield having a symmetric array of exploded mines. Or a pattern of murders by a serial killer.
But how do we know the pattern is not controlling us? — Gregory
Do you mean that by simply contemplating a pattern it might somehow control us? Or at least influence our thinking? Like mandalas?
Wiki: "In various spiritual traditions, mandalas may be employed for focusing attention of practitioners and adepts, as a spiritual guidance tool, for establishing a sacred space and as an aid to meditation and trance induction." -
TheMadFool
13.8kThe word "random" is used in two very related ones. It can mean "spontaneous action" such that world seems to act as if it has free will but no consciousness, and it can mean irregular patterns. I am wondering if the latter is based on anything objective. We all have different tastes in physical appearances. Someone might seem beautiful to someone else, but not to a third person. We all have different tastes in art and music as well. Further, autistic people see patterns within disorder. What is one person's order is another person's mess. Therefore, IQ tests seem to measure how a person scores within an arbitrarily assigned range of what is "smart". If I have a sequence 2,4,8 and ask what comes next, any answer can be right. What if it is the law of the human nature that after two doublings you multiply by 100. The answer would be 800. What if that was the law of just some peoples' genes? They would score low on an IQ test. But the IQ test is not objective then. If beauty is in the eye of the beholder, than so is order.
In conclusion, is chaos theory all bunk? — Gregory
The word "random", to me, indicates a systems state where every possible outcome is equi-probable. For instance a die is random if every outcome: 1, 2, 3, 4, 5, and 6, is equally likely.
Once, given a system of outcomes, some outcomes become more probable then that system isn't random. That said, consider a pair of die and you'll notice certain sums of outcomes in throwing them together, despite each individual outcome actually being totally random, have a greater probability of occurring. Does this mean that the 2-dice system isn't random? No, because we have an explanation for why some outcomes are more likely even in a completely random system. In the case of the 2-dice system we need only look at how many ways a particular outcome can occur and if there are more ways to get outcome x then x will occur with that frequency.
So, randomness isn't simply a matter of equi-probability; although if the presence of some favored/some disfavored outcomes can be explained by an underlying random process it is.
Chaos theory, as I understand it, seems to be about small changes in a system resulting in large deviations in outcomes. The classic example is that of the small air disturbances caused by a butterfly leading to storms in far off, distant places. I believe Lorenz, who coined the term the butterfly effect, had entered data that differed only in the hundredth or thousandth decimal place and the outcomes for these inputs that differed in such small degrees produced large variations in the output, whatever that was. Data was fed into a system, probably a set of deterministic functions, but the functions spat out numbers that differed by massive amounts. It's this effect of small changes causing large differences in outcome that chaos theory is all about (in my opinion).Chaos theory isn't about randomness per se but is, in essence, a difficulty we face in making predictions about chaotic systems. -
 jgill
4kWiki: "Chaos theory is a branch of mathematics focusing on the study of chaos—states of dynamical systems whose apparently-random states of disorder and irregularities are often governed by deterministic laws that are highly sensitive to initial conditions."
jgill
4kWiki: "Chaos theory is a branch of mathematics focusing on the study of chaos—states of dynamical systems whose apparently-random states of disorder and irregularities are often governed by deterministic laws that are highly sensitive to initial conditions."
The article goes on to state that it is an interdisciplinary area, however. "Chaotic behavior" might be more accurate outside the mathematical umbrella. Using "theory" makes the concept more formal and technical. Just my two bits. :smile: -
 Gregory
5k
Gregory
5k
Chaos behavior is about "patterns" in randomness. How could "some outcomes are more likely even in a completely random system".? I think we sense patterns based on beauty only. If I cut a square into four triangles, can you prove it has more "pattern" than a white sheet of paper with one dot in the corner? Is it more patterned if the dot is in the middle? If beauty is in the soul of the beholder, then even pattern might not inherently out there. -
 Gregory
5kSpinoza and Leibniz thought everything was controlled by one principle. Infinity in substance, which far outstrips when you count to infinity and call it infinity. Occasionalism is a much better option. Did Einstein believe in compatabism. Spinoza was a determinalist. Either way the subjective and objective don't interact. When you say the first principle is impersonal or even nothingness personified, patterns cease
Gregory
5kSpinoza and Leibniz thought everything was controlled by one principle. Infinity in substance, which far outstrips when you count to infinity and call it infinity. Occasionalism is a much better option. Did Einstein believe in compatabism. Spinoza was a determinalist. Either way the subjective and objective don't interact. When you say the first principle is impersonal or even nothingness personified, patterns cease -
TheMadFool
13.8kChaos behavior is about "patterns" in randomness. How could "some outcomes are more likely even in a completely random system".? I think we sense patterns based on beauty only. If I cut a square into four triangles, can you prove it has more "pattern" than a white sheet of paper with one dot in the corner? Is it more patterned if the dot is in the middle? If beauty is in the soul of the beholder, then even pattern might not inherently out there. — Gregory
I'm not quite sure about that. To begin with I don't think chaos, as conventionally understood, is about patterns; quite to the contrary, when a system exhibits no discernible pattern it is said to be in chaos. However, I'm willing to entertain the possibility that chaos may be construed as a completely random system.
Secondly, the only subject that studies patterns seriously is math and I don't know if there's a subfield devoted to just the study of patterns or not. -
 Gregory
5kIf I roll a dice a zillion times, each roll is one and six that I will come up with a 6. So the same applies the zillion (one to one correspondence). Strict logic seems to say the world does work by determinism and Einstein was right therefore. If the laws suddenly "changed" because we didn't really understand them, the scientists would say a new force has enter our universe. Hume would say "what's the difference, what is force", and he might be right
Gregory
5kIf I roll a dice a zillion times, each roll is one and six that I will come up with a 6. So the same applies the zillion (one to one correspondence). Strict logic seems to say the world does work by determinism and Einstein was right therefore. If the laws suddenly "changed" because we didn't really understand them, the scientists would say a new force has enter our universe. Hume would say "what's the difference, what is force", and he might be right -
 jgill
4kSecondly, the only subject that studies patterns seriously is math and I don't know if there's a subfield devoted to just the study of patterns or not. — TheMadFool
jgill
4kSecondly, the only subject that studies patterns seriously is math and I don't know if there's a subfield devoted to just the study of patterns or not. — TheMadFool
https://www.maa.org/press/periodicals/convergence/mathematics-as-the-science-of-patterns-mathematics-as-the-science-of-patterns :cool: -
 Gregory
5kEinstein's position was self refuting. If things are all determined you can't even do science because the law might be that the after an age a new age with the opposite laws appear. You can never catch the universe red handed. Can the determined become random or the random become determinef. Nobody knows.
Gregory
5kEinstein's position was self refuting. If things are all determined you can't even do science because the law might be that the after an age a new age with the opposite laws appear. You can never catch the universe red handed. Can the determined become random or the random become determinef. Nobody knows. -
 Agent Smith
9.5kTo Mathematicians
Agent Smith
9.5kTo Mathematicians
Is Chaos Theory (math) an admission that the calculations involved are too complex for humans and current top-of-the-line supercomputers (extremely difficult to predict) or is the claim that there's true randomness (unpredictability).
Note: There's a difference between computational complexity (difficult to prognosticate) and randomness (impossible to prognosticate) -
 Haglund
802
Haglund
802
Chaos theory is about sensitivity to initial conditions. Vary them a tiny bit and you might end up in Bakerstreet instead of Trafalgar Square. -
 Agent Smith
9.5kChaos theory is about sensitivity to initial conditions. Vary them a tiny bit and you might end up in Bakerstreet instead of Trafalgar Square — Haglund
Agent Smith
9.5kChaos theory is about sensitivity to initial conditions. Vary them a tiny bit and you might end up in Bakerstreet instead of Trafalgar Square — Haglund
You say it better than the mathematicians! :up: -
 jgill
4kTo Mathematicians
jgill
4kTo Mathematicians
Is Chaos Theory (math) an admission that the calculations involved are too complex for humans and current top-of-the-line supercomputers (extremely difficult to predict) or is the claim that there's true randomness (unpredictability). — Agent Smith
The computer calculations define the dynamical system in C (complex plane). Iteration of a function carries an initial point in C to a new position - usually not the same position unless the original point is a fixed point of the function. When there is a condition in which two points very close to one another diverge dramatically and relatively unpredictably under iteration the system may be chaotic (under other circumstances fractals might appear). This might occur everywhere on a set S in C, or on a part of S. This is the simplest version of chaos theory. Draw your own conclusions. :cool: -
 Agent Smith
9.5kIs the unpredictability absolute i.e. is it impossible to predict or is it just that we don't have powerful enough supercomputers i.e. unpredictability is relative, possible but not with current tech?
Agent Smith
9.5kIs the unpredictability absolute i.e. is it impossible to predict or is it just that we don't have powerful enough supercomputers i.e. unpredictability is relative, possible but not with current tech? -
 jgill
4kHere is a non-chaotic image arising from an iteration process that involves differing functions rather than a single function. Its' beautiful intricacies might possibly be predictable were an attempt made to do so, but it would take a significant effort. This is a dynamical system in C that rewards its inventor. I call it Dream of Gold.
jgill
4kHere is a non-chaotic image arising from an iteration process that involves differing functions rather than a single function. Its' beautiful intricacies might possibly be predictable were an attempt made to do so, but it would take a significant effort. This is a dynamical system in C that rewards its inventor. I call it Dream of Gold.

-
 jgill
4kCan you zoom in like in those colored fractal zoomings (where the colors represent a rate of convergence, if Im not mistaken)? — Haglund
jgill
4kCan you zoom in like in those colored fractal zoomings (where the colors represent a rate of convergence, if Im not mistaken)? — Haglund
It's not a fractal, but sometimes one can focus on a spot and enlarge it and find additional intricacies. Iterations are done at pixel levels with light shades when the modulus is great and dark shades when it is small. Very simple.
↪jgill
Impressive. This is yours? — Banno
Yes, I've done lots of unpredictable images. Look at my icon on TPF. Here's another I call Reproductive Universe:
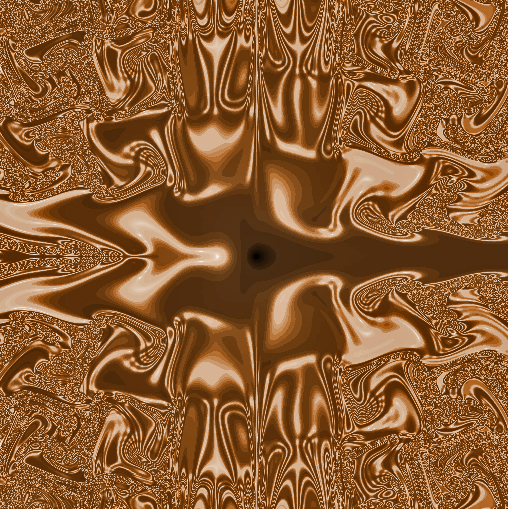
-
 Cuthbert
1.1k@jgill Amazing images, thank you!
Cuthbert
1.1k@jgill Amazing images, thank you!
For non-programmers with basic skills (me), there is a way to explore chaos with a simple iterative function on a calculator or in Excel.
Begin with a number between 0 and 1 in the first cell. Next cell = previous cell x (1 - previous cell) x some constant between 2 and 4. Copy down a few hundred times. Graph the outputs.
Then play with the constant, say starting at 2.5 and raising it 0.01 at a time. The graph will begin as a flat line, then split into peaks and troughs, repeating every second output, period 2, then every fourth, eighth etc output - then it will become non-repeating apparent disorder with bursts of order, e.g. period 3 or 5.
This reproduces one of the ways Feigenbaum used to investigate chaos. I think he started with a calculator, not even a graphed spreadsheet. https://www.youtube.com/watch?v=ETrYE4MdoLQ
No randomness is involved here. It's sometimes confusing because the concept 'chaos' suggests randomness but 'chaos theory' is about sensitivity to initial conditions in a deterministic system. -
 jgill
4kBegin with a number between 0 and 1 in the first cell. Next cell = previous cell x (1 - previous cell) x some constant between 2 and 4. — Cuthbert
jgill
4kBegin with a number between 0 and 1 in the first cell. Next cell = previous cell x (1 - previous cell) x some constant between 2 and 4. — Cuthbert
Sound like elementary cellular automata, championed by Wolfram some time ago. I've written programs that show a constant sort of development, then a jump to a weird line or something. Wolfram thought he had come upon a hugely important concept, writing a book with over a thousand pages. I, like most other readers, gave up after a few hundred pages.
Somehow they seem to eat each other. Raw sex in the complex plane... — Haglund
Like Pac-Men. My friend, you need to get out of the house more often. :wink: -
 Haglund
802
Haglund
802
The dog pulled my arm. Luckily she didn't take puppy course. She is always eager to go to the park. Pulling me along (which I'm fine with, it shows life!). Knowing I'm gonna swing away the biggest treetrunks! With that same right arm she's pulling... Something in my shoulder is stretched too long, I guess... Time heals everything, I hope! :wink:
I guess it pales in the face of your accident about 35 years ago... -
 Agent Smith
9.5kLooks very Mayan! Perhaps its just the combination of color and the swirling motif.
Agent Smith
9.5kLooks very Mayan! Perhaps its just the combination of color and the swirling motif. -
 Haglund
802
Haglund
802
Have you seen his other works? Out of this world! Seems he had an encounter with the gods, high up those mountains he bouldered! -
 jgill
4kI guess it pales in the face of your accident about 35 years ago... — Haglund
jgill
4kI guess it pales in the face of your accident about 35 years ago... — Haglund
Sadly that's the strongest part of my body now. :worry:
↪jgill
Looks very Mayan! Perhaps its just the combination of color and the swirling motif. — Agent Smith
Hidden within those intricate folds are the secrets of the universe.
Well, maybe not. :sad:
Welcome to The Philosophy Forum!
Get involved in philosophical discussions about knowledge, truth, language, consciousness, science, politics, religion, logic and mathematics, art, history, and lots more. No ads, no clutter, and very little agreement — just fascinating conversations.
Categories
- Guest category
- Phil. Writing Challenge - June 2025
- The Lounge
- General Philosophy
- Metaphysics & Epistemology
- Philosophy of Mind
- Ethics
- Political Philosophy
- Philosophy of Art
- Logic & Philosophy of Mathematics
- Philosophy of Religion
- Philosophy of Science
- Philosophy of Language
- Interesting Stuff
- Politics and Current Affairs
- Humanities and Social Sciences
- Science and Technology
- Non-English Discussion
- German Discussion
- Spanish Discussion
- Learning Centre
- Resources
- Books and Papers
- Reading groups
- Questions
- Guest Speakers
- David Pearce
- Massimo Pigliucci
- Debates
- Debate Proposals
- Debate Discussion
- Feedback
- Article submissions
- About TPF
- Help
More Discussions
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum





