-
 Philosopher19
279If x, y, and z are sets that are not members of themselves, and I form a set of these three sets, to represent this, I can write something like: p = {x, y, z}. I cannot write x = {x, y, z}.
Philosopher19
279If x, y, and z are sets that are not members of themselves, and I form a set of these three sets, to represent this, I can write something like: p = {x, y, z}. I cannot write x = {x, y, z}.
If x, y, and z are sets that are members of themselves, and I form a set of these three sets, to represent this, I can write something like: p = {x, y, z}. I cannot write x = {x, y, z}.
You cannot have a set of ALL sets that are not members of themselves because it will result in at least one set not being included in the set. In other words, x will have to be in x, but it can't.
You cannot have a set of ALL sets that are members of themselves because it will result in at least one set being a member of itself twice. In other words, x will have to not be in x, but it can't.
For the solution to Russell's paradox:
http://philosophyneedsgods.com/2021/05/22/the-solution-to-russells-paradox-and-the-absurdity-of-more-than-one-infinity/ -
 Amalac
489I cannot write x = {x, y, z}. — Philosopher19
Amalac
489I cannot write x = {x, y, z}. — Philosopher19
If y and z are members of x, then you actually can write it (if a set can be a member of itself). (I'm refering to the part where you say x is a member of itself).
You cannot have a set of ALL sets that are not members of themselves because it will result in at least one set not being included in the set. In other words, x will have to be in x, but it can't. — Philosopher19
The idea that such a set can't be constructed to solve the paradox does seem correct, as Russell's own solution (the theory of types) maintains.
But your reason for holding that there can't be such a set seems inadequate, all you are doing is to re-state the paradox: If x can't be in x then, by definition, it would have to be in x, since it would be a set that doesn't contain itself.
It's easier to understand with Grelling's paradox, which is similar to Russell's:
Suppose we define an adjective that describes itself as an autological adjective. For example: “polysyllabic” is a polysyllabic adjective, therefore it is autological.
And suppose we define an adjective that does not describe itself as a heterological adjective. For example: “monosyllabic” is not monosyllabic, therefore it is a heterological adjective.
But then the question arises: Is “heterological” a heterological adjective?
Let's say we maintain that it is, that means “heterological” is an adjective that does not describe itself. But if that's the case, then the adjective in question must not be named “heterological”, for that would necessarily imply that it describes itself. Yet we know that it is named “heterological”, therefore it can't be heterological.
Let's now maintain that it isn't heterological (that it's autological), meaning it does describe itself: That implies that it is heterological, since otherwise it would not describe itself. But obviously it is a contradiction to maintain that “heterological” both is and is not a heterological adjective. Therefore it can't be the case that it is autological either. -
 TonesInDeepFreeze
3.8kIf x, y, and z are sets that are members of themselves, and I form a set of these three sets, to represent this, I can write something like: p = {x, y, z}. I cannot write x = {x, y, z}. — Philosopher19
TonesInDeepFreeze
3.8kIf x, y, and z are sets that are members of themselves, and I form a set of these three sets, to represent this, I can write something like: p = {x, y, z}. I cannot write x = {x, y, z}. — Philosopher19
That is incorrect.
Of course, to countenance sets being member of themselves, we have to delete the axiom of regularity. With that done:
Suppose xex, yey, and zez
Suppose x = {x y z}
Those suppositions together are consistent. For example by letting:
y = {y} and z = {z}
You cannot have a set of ALL sets that are not members of themselves — Philosopher19
With the axiom of regularity, that is correct, since such a set would have all sets as members, from which we derive a contradiction.
The Russell principle though is:
There is no set of all and only the sets that are not members of themselves.
And that is derived from first order logic alone:
For any relation R, ~ExAy(Ryx <-> ~Ryy)
You cannot have a set of ALL sets that are members of themselves — Philosopher19
That is incorrect. With the axiom of regularity, that set is the empty set. And without the axiom of regularity, it would still be consistent for there to be a non-empty set of all sets that are members of themselves. For example, allow that there is just one set S that is a member of itself. Then the set of all sets that are members of themselves is {S}. -
 fishfry
3.4kThat is incorrect. With the axiom of regularity, that set is the empty set. And without the axiom of regularity, it would still be consistent for there to be a non-empty set of all sets that are members of themselves. For example, allow that there is just one set S that is a member of itself. Then the set of all sets that are members of themselves is {S}. — TonesInDeepFreeze
fishfry
3.4kThat is incorrect. With the axiom of regularity, that set is the empty set. And without the axiom of regularity, it would still be consistent for there to be a non-empty set of all sets that are members of themselves. For example, allow that there is just one set S that is a member of itself. Then the set of all sets that are members of themselves is {S}. — TonesInDeepFreeze
Second this (almost). Here are the relevant links. Turns out that self-containing sets are an object of interest. However I do not believe there could be a set of all sets that contain themselves, even in the absence of regularity. Such a set would be subject to Russell's paradox.
https://en.wikipedia.org/wiki/Non-well-founded_set_theory
https://plato.stanford.edu/entries/nonwellfounded-set-theory/ -
 TonesInDeepFreeze
3.8kI do not believe there could be a set of all sets that contain themselves — fishfry
TonesInDeepFreeze
3.8kI do not believe there could be a set of all sets that contain themselves — fishfry
With regularity, It's the empty set.
And we can't derive a contradiction by dropping an axiom, so such a set is consistent also without regularity. But it would be inconsistent with set theory without regularity if every set were a member of itself, but "every set is a member of itself" is already inconsistent with set theory (even without regularity).
Such a set would be subject to Russell's paradox. — fishfry
Nope. -
 fishfry
3.4kWith regularity, It's the empty set.
fishfry
3.4kWith regularity, It's the empty set.
And we can't derive a contradiction by dropping an axiom, so such a set is consistent also without regularity. But it would be inconsistent with set theory without regularity if every set were a member of itself. — TonesInDeepFreeze
Hmmmm. Don't think this can work. If there's a set of all sets that contain themselves, then its complement is the set of all sets that don't contain themselves; which both does and does not contain itself. So this can't work.
Why not? Well to form a set via the axiom schema of specification, you need an existing set: where is a set and is a unary predicate.
You would like to form the set but you haven't got an existing set to start with, so this is not a legal set specification.
Of course you COULD form the set or , for example. Given any particular set, you can form the set of all its elements that are not elements of themselves, and the result (under regularity) will be the empty set. But you cannot form the set of ALL such sets, because you have no universal set with which to invoke specification.
What say you? I admit this is a tricky one but I've got myself 99.9% convinced of my own reasoning. -
 TonesInDeepFreeze
3.8kYou would like to form the set R={x:x∉x}R={x:x∉x} but you haven't got an existing set to start wit — fishfry
TonesInDeepFreeze
3.8kYou would like to form the set R={x:x∉x}R={x:x∉x} but you haven't got an existing set to start wit — fishfry
I don't think you mean {x | ~xex}. We're talking about {x | xex}.
And yes, without regularity, we can't prove there is a nonempty set {x | xex}.
But that's not the question. The question is whether we can prove that it is not the case that there is a set {x | xex}. And we can't. It is consistent with set theory that there is a set {x | xex}. And with regularity, it is provable that there is a set [x | xex}. -
 fishfry
3.4kSet theory does not allow taking a universal complement like that. — TonesInDeepFreeze
fishfry
3.4kSet theory does not allow taking a universal complement like that. — TonesInDeepFreeze
I'll retract that objection and reiterate my point that you cannot form the set absent some existing set. Which in your case needs to be the universal set, which does not exist. At best you can form the set for every set you can name. That's the best you can do. -
 TonesInDeepFreeze
3.8k
TonesInDeepFreeze
3.8k
Your math notation in your previous post does not format form me.
Anyway, {x | ~xex} is not at question. There is no such set. -
 fishfry
3.4kYour math notation in your previous post does not format form me. — TonesInDeepFreeze
fishfry
3.4kYour math notation in your previous post does not format form me. — TonesInDeepFreeze
It formats fine for me, but it took a couple of edits before it did. Is it still bad? Can't do anything about that, it looks right at my end.
Anyway, {x | ~xex} is not at question. There is no such set. — TonesInDeepFreeze
Then we're in agreement and you have conceded my point, since that is exactly the set you claim exists. Write out your claim formally and you'll get exactly what you just wrote.
I don't think you mean {x | ~xex}. We're talking about {x | xex}. — TonesInDeepFreeze
Yes ok, you're right, but that also is not a legal set specification.
"given a set A and a predicate P, we can find a subset B of A whose members are precisely the members of A that satisfy P."
https://en.wikipedia.org/wiki/Axiom_schema_of_specification#Statement
In order to form the set of all sets that are members of themselves, you have to start with some existing set and then apply specification to the predicate "x element of x". -
TheMadFool
13.8k
I thought Russell's paradox was meant to undermine set theory. As far as I can tell, it begins as C = the set of all sets that doesn't contain itself. Either C is itself in C or not. If C contains itself, C can't contain itself. If C doesn't contain itself, C contains itself. In short, C contains itself AND C doesn't contain itself. Contradiction.
Let's look at the issue as the conditionals they're said to be
1. If C contains itself then C doesn't contain itself
2. C doesn't contain itself or C doesn't contain itself (1 Imp)
3. C doesn't contain itself (2 Taut)
4. If C doesn't contain itself then C contains itself
5. C contains itself or C contains itself (4 Imp)
6. C contains itself (5 Taut)
Ergo,
7. C contains itself and C doesn't contain itself (3, 6 Conj) [Contradiction]
But then, Russell's argument boils down to,
3. C doesn't contain itself
6. C contain itself
8. C contains itself and C doesn't contain itself (3, 6 conj)
Ergo,
9. C contains itself (deny 3)
Or
10. C doesn't contain itself (deny 6)
Both 3 and 6 can't be denied...leads to a contradiction.
It's a tautology, C contains itself or C doesn't contain itsellf. There's no contradiction! -
 TonesInDeepFreeze
3.8kIs it still bad? — fishfry
TonesInDeepFreeze
3.8kIs it still bad? — fishfry
Looks okay now.
Then we're in agreement and you have conceded my point, since that is exactly the set you claim exists. — fishfry
No, I don't. Indeed, I said the opposite in my original post.
Write out your claim formally and you'll get exactly what you just wrote. — fishfry
Howzabout you quote me where you think I claimed that there exists a set whose members are all and only the sets that are not members of themselves.
Indeed, I pointed out that there is not such a set, and even on logical principles alone.
that also is not a legal set specification. — fishfry
It doesn't depend on the abstraction operator. I could just as well write the whole conversation without the abstraction operator.
In order to form the set of all sets that are members of themselves, you have to start with some existing set and then apply specification to the predicate "x element of x". — fishfry
To prove the existence of sets having a certain property, we can only use the axioms. But the axioms don't say that other sets don't exist, except as we can prove from the axioms that there do not exist sets of a certain property.
Again, the axioms don't prove that there does not a exist a set whose members are all and only those sets that are members of themselves. Indeed, with regularity, the axioms prove that here does exist such a set. -
 fishfry
3.4kI thought Russell's paradox was meant to undermine set theory. — TheMadFool
fishfry
3.4kI thought Russell's paradox was meant to undermine set theory. — TheMadFool
It undermined Frege's idea that a set is defined by a predicate, as in "the set of things satisfying such and so." That leads to a contradiction. The fix is to require that the predicate must be applied to an already existing set, as in "the set of things in some set X that satisfy such and so." This is the meaning of the axiom schema of specification.
"given a set A and a predicate P, we can find a subset B of A whose members are precisely the members of A that satisfy P."
https://en.wikipedia.org/wiki/Axiom_schema_of_specification
In symbols, if we know we have some set , we can form the set where P is some predicate.
But we can NOT form the set , that gets us into Russell trouble. -
 fishfry
3.4kLooks okay now. — TonesInDeepFreeze
fishfry
3.4kLooks okay now. — TonesInDeepFreeze
Good, thanks.
No, I don't. — TonesInDeepFreeze
My head hurts but I think I'm right. Let's see what comes next ...
It doesn't depend on the abstraction operator. I could just as well write the whole conversation without the abstraction operator. — TonesInDeepFreeze
Then do so. Let me see it. Writing it in words doesn't help. "The set of sets that are members of themselves." It's true that there aren't any such sets (under regularity). But it does NOT mean there is a set of them. So if you claim there is a SET of them, let me see a legal set specification.
Again: Yes I agree that under regularity, there are no sets that are members of themselves. But there is NOT a SET of all sets that are members of themselves, not even the empty set. Though I agree that it's a bit of a puzzler. To solve it you have to get very formal. Show me a valid set specification that supports your claim and I'll believe you.
To prove the existence of sets having a certain property, we can only use the axioms. But the axioms don't say that other sets don't exist, except as we can prove from the axioms that there do not exist sets of a certain property. — TonesInDeepFreeze
You can't form the set you claim exists. So you are saying that some set exists that's not given by the axioms? That's a stretch. Explain this a bit more.
Again, the axioms don't prove that there does not a exist a set whose members are all and only those sets that are members of themselves. Indeed, with regularity, the axioms prove that here does exist such a set. — TonesInDeepFreeze
So you agree you can't prove that your set exists, but you claim it exists anyway? Is that your argument? You might almost have an argument, I want to make sure I'm understanding you.
Let me restate your argument. The empty set is the set of all flying purple elephants. And the empty set is the set of all sets that contain themselves under regularity.
Perhaps you've convinced me. Is that what you mean? You could be right.
In order to object to this argument, I have to say that the set of all flying purple elephants is also not a legal set. The set of all flying purple elephants that are animals is the empty set. And if I get pedantic that way about the axiom schema of specification, then your argument fails. But I admit it's not an entirely bad argument. -
 TonesInDeepFreeze
3.8kI thought Russell's paradox was meant to undermine set theory. — TheMadFool
TonesInDeepFreeze
3.8kI thought Russell's paradox was meant to undermine set theory. — TheMadFool
Russell's paradox shows the contradiction in set theory with unrestricted comprehension. After Russell's note, we moved to a set theory that does not have unrestricted comprehension.
What follows as of necessity? — TheMadFool
That there does not exist such a set.
I believe the liar sentence too is treated in a similar way - banished from the world of propositions.
If you can formalize that for mathematics, fine. But meanwhile, ordinary mathematical logic and set theory do not "ban" such a formulation.
(1) In set theory, we don't ban writing "ExAy(yex <-> ~yey)". Rather, we prove ~ExAy(yex <-> ~yey).
(2) In mathematical logic, we don't dispute that some theories may formalize a liar-like sentence. Rather, we prove that any theory that can do so is inconsistent. -
 fishfry
3.4kRussell's paradox shows the contradiction in set theory with unrestricted comprehension. After Russell's note, we moved to a set theory that does not have unrestricted comprehension. — TonesInDeepFreeze
fishfry
3.4kRussell's paradox shows the contradiction in set theory with unrestricted comprehension. After Russell's note, we moved to a set theory that does not have unrestricted comprehension. — TonesInDeepFreeze
Yes correct! Exactly. But you are also claiming that "the set of all sets that are members of themselves" exists and is the empty set. That's not consistent with what you just said! You can't invoke unrestricted comprehension. All you've done is remind me that when I tell people that "the empty set is the set of all purple, flying elephants," I'm violating the axiom schema of specification. But at least I'm doing it for a good cause :-) -
 TonesInDeepFreeze
3.8kThen do so. Let me see it. — fishfry
TonesInDeepFreeze
3.8kThen do so. Let me see it. — fishfry
Are you serious? Come on, you know how to do it yourself:
ZF |- ~ExAy(yex <-> ~yey)
ZF |/- ~ExAy(yex <-> yey).
ZF-R |/- ~ExAy(yex <-> yey)
ZF |- ExAy(yex <-> yey)
ZF-R |/- ExAy(yex <-> yey)
/
But there is NOT a SET of all sets that are members of themselves, not even the empty set. — fishfry
With regularity, yes the empty set 0.
E!yAx(xey <-> yey_
In English: There exists a unique set whose members are all and only those sets that are members of themselves. Proof:
xe0 <-> xex
So Ax(xe0 <-> xex)
So E!y(xey <-> xex)
So 0 = the-y Ax(xey <-> xex) = {x | xex}
So you are saying that some set exists that's not given by the axioms? — fishfry
No, I am not. Read what I said. I said that we can only prove existence from the axioms. But we can't prove non-existence from the axioms except when the axioms actually prove the non-existence. And in the case of ZF-R, the axioms don't prove the non-existence of a set whose members are all and only those sets that are members of themselves. And with ZF, the axioms do prove there is such a set; it's the empty set. -
 TonesInDeepFreeze
3.8kYou can't invoke unrestricted comprehension. — fishfry
TonesInDeepFreeze
3.8kYou can't invoke unrestricted comprehension. — fishfry
I didn't.
All you've done is remind me that when I tell people that "the empty set is the set of all purple, flying elephants," I'm violating the axiom schema of specification. — fishfry
No, I'm not violating separation. Separation and extensionality were used to prove the existence of 0 (in an axiomatization where the existence of an empty set is not taken as an axiom).
To prove the existence of a set, we don't always have to do it directly from separation. We have union, power set, etc. But in this case I did prove it from separation, extensionality, and whaever other axioms prove ~Ex xex from regularity, as separation was used in the previous result that ExAy ~yex. -
 fishfry
3.4kTo prove the existence of a set, we don't always have to do it directly from separation. We have union, power set, etc. But in this case I did prove it from just separation, extensionality, and regularity, as separation was used in the previous result that ExAy ~yex. — TonesInDeepFreeze
fishfry
3.4kTo prove the existence of a set, we don't always have to do it directly from separation. We have union, power set, etc. But in this case I did prove it from just separation, extensionality, and regularity, as separation was used in the previous result that ExAy ~yex. — TonesInDeepFreeze
I'll try to go through your proof later. I'd prefer it if you'd mark it up but I'll slog through the ASCII later maybe. I think you are making an interesting point. You might be right after all, I'm not sure. -
 TonesInDeepFreeze
3.8k
TonesInDeepFreeze
3.8k -
 TonesInDeepFreeze
3.8k
TonesInDeepFreeze
3.8k
No, you know it.
(1) is set theory proving there is no set whose members are all and only those sets that are not members of themselves.
(2) is Tarski's theorem. -
 Philosopher19
279If y and z are members of x, then you actually can write it (if a set can be a member of itself). (I'm refering to the part where you say x is a member of itself). — Amalac
Philosopher19
279If y and z are members of x, then you actually can write it (if a set can be a member of itself). (I'm refering to the part where you say x is a member of itself). — Amalac
But my point is that x, y, and z are not members of themselves, whereas x = {x, y, z} means that x is a member of itself. Hence why I have to write something like p = {x, y, z} to represent x, y and z not being members of themselves.
But the key part of my post is that you cannot have a set of all sets that are members of themselves because it will result in at least one set being a member of itself twice. This is the overlooked part of Russell's paradox. -
 Philosopher19
279
Philosopher19
279
I'm going back to the root of the matter. The problem occurred because there wasn't enough clarity with regards to what it is for a set to be a member of itself, and what it is for a set to not be a member of itself.
Consider the following:
Call any set that is not a member of itself a -V. Call any set that is not the set of all sets a V'. Call any set that's simply a set, a V (the V of all Vs = the set of all sets).
Is the V of all -Vs a member of itself? It is impossible to have a V of all -Vs that contains all -Vs and no other sets. You cannot have a set of all sets that are not members of themselves that is itself not a member of itself. You cannot have a -V as a V of all -Vs.
No V, or V’, or -V, can contain all -Vs and nothing more, but one V can contain all -Vs and something more.
Two Vs contain all V's:
One (which is a V') contains all V's and nothing more. The other (which is not a V') contains all V's and something more. The latter is the set of all sets (the V of all Vs), the former is the V' of all V's (the not-the-set-of-all-sets set of all not-the-set-of-all-sets sets). Thus, only one V can
contain all Vs and nothing more (the V of all Vs). Only one V' can contain all V's and nothing more (the V' of all V’s).
The above shows that whilst there can be no -V that contains all -Vs, there is a V that contains all -Vs. Whilst there can be two Vs that contain all -V’s, there can only be one V’ that contains all -V’s. -V and -V’ are semantically not the same. -V’ = any V’ set that is not a member of itself.
Rejecting the set of all sets is the last thing we should be doing, and it is a member of itself. See the link in the OP for a more detailed proof of this. -
 Philosopher19
279
Philosopher19
279
What if you view it this way:
The set of all sets encompasses all sets. It encompasses all sets that are not members of themselves, and it is a member of itself (because it encompasses itself). No contradictions here. See?
If interested, see the link in the OP for a more thorough discussion and solution of Russell's paradox. -
TheMadFool
13.8kNo, you know it.
(1) is set theory proving there is no set whose members are all and only those sets that are not members of themselves.
(2) is Tarski's theorem. — TonesInDeepFreeze
How about the following argument. Please go easy on me.
Suppose C = the set of all sets that don't contain itself
1. A set can contain itself like so A = {1, A} but there seems to be problem when you list down the elements. Suppose B is a set that contains itself:.{1, 2, {1, 2, {1, 2,..the task can't be completed. In other words, no set can contain itself. Ergo ALL sets are sets that don't contain themselves. Can we construct a set of all sets that don't contain themselves? Why not? Of course we can because ALL sets can't contain themselves. However, this set can't can't contain itself.
1. All sets don't contain themselves.
2. The set of all sets that don't contain themselves = The set of all sets.
3. The set of all sets is impossible because it can't be member of itself and so it can't be the set of all sets. (from 1)
4. The set of all sets that don't contain itself is also impossible (from 2 and 3).
5. For Russell's paradox, the set of all sets that don't contain itself must be a set.
6. The set of all sets that don't contain itself is impossible i.e. it isn't a set.
Ergo,
7. Russell's paradox is not a paradox. -
 Amalac
489
Amalac
489
If x, y, and z are sets that are members of themselves, and I form a set of these three sets, to represent this, I can write something like: p = {x, y, z}. I cannot write x = {x, y, z}. — Philosopher19
Here you say they are members of themselves. If they are members of themselves, then x can be contained in x, right? So if set y and set z are members of x, what’s the problem with writing that the set x contains sets x, y and z?
If y and z are not members of x, then obviously they cannot be contained in x, but x can still be contained in itself.
But the key part of my post is that you cannot have a set of all sets that are members of themselves because it will result in at least one set being a member of itself twice. This is the overlooked part of Russell's paradox. — Philosopher19
Suppose x is the set of all ideas: since the set of all ideas is itself an idea, it contains itself. What’s wrong with that? I guess you are saying that if the set of all ideas contained itself, then the set of all ideas contained in the set of all ideas would also have to contain the set of all ideas again, and so on in infinitum. Well yes, but what’s wrong with that?
Using a mathematical analogy: the golden ratio’s infinite radical and its continued fraction contain themselves infinitely many times, and yet that does not give rise to any contradictions:
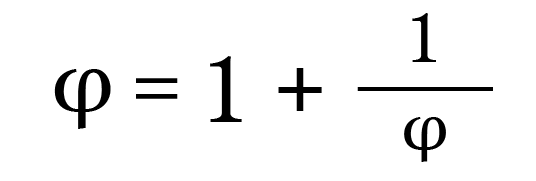
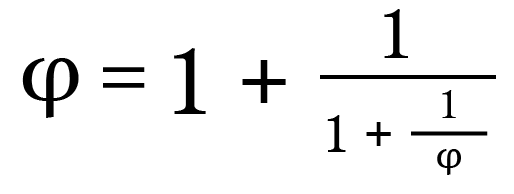
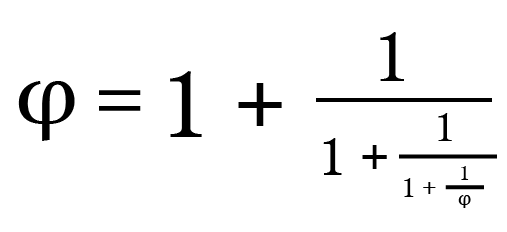
... and so on forever. -
 TonesInDeepFreeze
3.8kyou cannot have a set of all sets that are members of themselves — Philosopher19
TonesInDeepFreeze
3.8kyou cannot have a set of all sets that are members of themselves — Philosopher19
With regularity, there is a set whose members are all and only those sets that are members of themselves. That set is the empty set. And if we drop regularity, then the statement that there is a set whose members are all and only those sets that are members of themselves is independent of the axioms.
it will result in at least one set being a member of itself twice — Philosopher19
'member of itself twice' has no apparent mathematical meaning. -
 Philosopher19
279Here you say they are members of themselves. If they are members of themselves, then x can be contained in x, right? — Amalac
Philosopher19
279Here you say they are members of themselves. If they are members of themselves, then x can be contained in x, right? — Amalac
That's the part I believe everyone has overlooked. I will try and show this clearly:
x, y and z, are sets that are not members of themselves. I am trying to form a set of these three sets that are not members of themselves.
A) It cannot be the case that x = {x, y, z} because that implies x is a member of itself, precisely because x is in x. But it can be the case that p = {x, y, z} precisely because x is not in x.
Now consider this: x, y, and z, are sets that are members of themselves. Consistency with A would have us say it cannot be the case that x = {x, y, z} precisely because x is in x. This either means that y and z are not members of themselves, or it means that y and z are members of themselves once, whilst x is a member of itself twice. Do you see my point with consistency? If I wrote p = {x, y, z} then you could say x, y, and z, are members of themselves precisely because x is not in x.
A set of all sets that are not members of themselves is impossible precisely because one set will have to be a member of itself. In other words, x will have to be in x, but it can't.
A set of all sets that are members of themselves is impossible precisely because one set will have to be a member of itself twice. In other words, x will have to be in x, but it can't because that would either amount to x being a member of itself twice (with all other sets being members of themselves once), or it would amount to x being a member of itself once, with all other sets not being members of themselves.
I am trying to bring consistency where I have seen inconsistency in mainstream set theory. Do you see the inconsistency in saying "you cannot have a set of all sets that are not members of themselves, but you can have a set of all sets that are members of themselves".
Once the above inconsistency is dealt with, we can see that the set of all sets is a member of itself, and it encompasses all sets that are not members of themselves (as well as itself). Note that this statement is not contradictory. Note that saying there can be no set that encompasses all sets is blatantly contradictory (and set theorists know this, they just haven't realised what they've overlooked). Again, the link in the OP covers this in more detail. -
 Philosopher19
279'member of itself twice' has no apparent mathematical meaning. — TonesInDeepFreeze
Philosopher19
279'member of itself twice' has no apparent mathematical meaning. — TonesInDeepFreeze
Yes I know. It's a contradiction for something to be a member of itself twice. I am saying that this is the logical consequence of a set of all sets that are members of themselves as proven here:
x, y and z, are sets that are not members of themselves. I am trying to form a set of these three sets that are not members of themselves.
A) It cannot be the case that x = {x, y, z} because that implies x is a member of itself, precisely because x is in x. But it can be the case that p = {x, y, z} precisely because x is not in x.
Now consider this: x, y, and z, are sets that are members of themselves. Consistency with A would be such that it cannot be the case that x = {x, y, z} precisely because x is in x. If we are to be consistent with A, then this either means that y and z are not members of themselves, or it means that y and z are members of themselves once, whilst x is a member of itself twice. Do you see my point?
A set of all sets that are not members of themselves is impossible precisely because one set will have to be a member of itself. In other words, x will have to be in x, but it can't.
A set of all sets that are members of themselves is impossible precisely because one set will have to be a member of itself twice. In other words, x will have to be in x, but it can't because that would either amount to x being a member of itself twice (with all other sets being members of themselves once), or it would amount to x being a member of itself once, with all other sets not being members of themselves. -
 Amalac
489That's the part I believe everyone has overlooked. I will try and show this clearly:
Amalac
489That's the part I believe everyone has overlooked. I will try and show this clearly:
x, y and z, are sets that are not members of themselves. I am trying to form a set of these three sets that are not members of themselves. — Philosopher19
In your OP you mention 2 possibilities:
1.x, y and z not being members of themselves.
2. x, y and z being members of themselves.
Then you say: if 1 is true then U follows, If 2 is true then P follows.
I'm refering only to the second possibility, in which we assume that x,y and z are members of themselves, and then we see what that would logically entail (P).
You say:If x, y, and z are sets that are members of themselves, and I form a set of these three sets, to represent this, I can write something like: p = {x, y, z}. I cannot write x = {x, y, z}. — Philosopher19
So you say if 2 is true, then x would be a member of itself, then we could write x={x,y,z} ,which we can't do because...well, you've given no reason to accept that yet, except that x would “contain itself twice”, which, if you mean what I said earlier (otherwise I don't know what you mean by that), is no reason for supposing that you can't have a set that contains itself as a member, in the same way as there is no contradiction about the golden ratio's continued fraction containing itself not just twice, but infinitely many times.
As for “the set of all sets that contain themselves”, regardless of whether or not such a set can be constructed, you have not yet given a good reason for maintaining that it can't be.
Welcome to The Philosophy Forum!
Get involved in philosophical discussions about knowledge, truth, language, consciousness, science, politics, religion, logic and mathematics, art, history, and lots more. No ads, no clutter, and very little agreement — just fascinating conversations.
Categories
- Guest category
- Phil. Writing Challenge - June 2025
- The Lounge
- General Philosophy
- Metaphysics & Epistemology
- Philosophy of Mind
- Ethics
- Political Philosophy
- Philosophy of Art
- Logic & Philosophy of Mathematics
- Philosophy of Religion
- Philosophy of Science
- Philosophy of Language
- Interesting Stuff
- Politics and Current Affairs
- Humanities and Social Sciences
- Science and Technology
- Non-English Discussion
- German Discussion
- Spanish Discussion
- Learning Centre
- Resources
- Books and Papers
- Reading groups
- Questions
- Guest Speakers
- David Pearce
- Massimo Pigliucci
- Debates
- Debate Proposals
- Debate Discussion
- Feedback
- Article submissions
- About TPF
- Help
More Discussions
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum



