-
 noAxioms
1.7kWe can remove GR from consideration by application of the equivalence principle to remove all mass and gravity from consideration, and then use this to illustrate the lack of transformation from one coordinate system to another.
noAxioms
1.7kWe can remove GR from consideration by application of the equivalence principle to remove all mass and gravity from consideration, and then use this to illustrate the lack of transformation from one coordinate system to another.
So acceleration is equivalent to gravity, so our space station hovering at 1g outside the black hole can be equivalent to the Rindler scenario where there is only acceleration and no significant mass/gravity anywhere in flat Minkowski spacetime, which can be described using SR rules.
So consider a coordinate system of a long rigid spaceship with meter markings on the sides that acts as our coordinate system. At the origin (the place marked zero), it is accelerating at a continuous 1g. Does this ship's coordinate system map all of spacetime? No, it does not. Acceleration of the ship is greater the further 'down' the length you go, until a limit is reached (about a lightyear from the origin in this case) at the event horizon (called the Rindler horizon).The ship cannot extend further back than this, but in can extend indefinitely in the 'up' direction. A clock dropped from the origin will fall past the ship and appear to freeze as it approaches that event horizon in the coordinate space of the ship. Light from events beyond this horizon can never reach any part of the ship, which means that while I accelerate at 1g, light from about a light year away will never reach me.
The events beyond that horizon do not exist (cannot be meaningfully ordered) in the coordinate space of the ship, and thus there exists no transform between them. Events there cannot be meaningfully placed on the timeline of the ship.
Of course, in the frame of the dropped clock, the rear of the ship passes it by without notice and the clock ticks on. Now from the perspective of the clock beyond the ship's event horizon, there is no event horizon at all. It is merely a coordinate singularity and not a physical singularity. Similarly, a black hole event horizon is a coordinate singularity. That means that from the perspective of beyond the horizon (the falling clock), the space on either side of the horizon can be mapped in a coherent coordinate system (that of the falling clock in this case). So there does exist a mapping between 'inside' and 'outside' so to speak, at least in the Rindler case, but only relative to an inertial (falling) reference. There is no physical singularity in the acceleration scenario, and there is one in the black hole case, and also there's the fact that no object can be falling into more than one black hole, so there seems to be no coordinate system that maps more than one of them. -
 noAxioms
1.7k
noAxioms
1.7k
Let me put it this way:If someone outside the hole applies the appropriate transformations to their forever-falling astronaut, they will find that form the astronaut's perspective the fall is finite.
If the astronaut applies the appropriate transformation, they will find that for someone outside the hoel the fall takes forever - or more.
I don't see any inconsistency. What did I miss? — Banno
P1 Time is absolute. There is an absolute ordering of all events in all of spacetime.
C1: For any event in spacetime and a given (time-like, or at least not space-like) worldline, that event is simultaneous with exactly one event on the given worldline.
C2: If, from the perspective of any particular observer, the simultaneity of two events does not correspond to C1, then that perspective does not correspond with reality. It is merely an abstract perspective.
Notice that it isn't necessary for any observer to be aware of this absolute time. We're just supposing there is one, not that it can be known for sure. Problem is, no coordinate system I can think of meets the requirement of C1, and the lack of the existence of such a coordinate system contradicts P1.
My choice of the first event is the falling clock when it reads 1 second beyond what it did as it crossed the event horizon. The first worldline is the clock hovering near that black hole, and a second worldline is a different clock falling into a different black hole.
How might one assign a time that is simultaneous with that first event on each of those two worldlines. The coordinate transformations you speak of seem not to exist, and at best they only transform between an abstract relation to the one actual one. I don't see the purpose of considering the abstract one at all. -
 Kenosha Kid
3.2kAcceleration of the ship is greater the further 'down' the length you go, until a limit is reached (about a lightyear from the origin in this case) at the event horizon (called the Rindler horizon). — noAxioms
Kenosha Kid
3.2kAcceleration of the ship is greater the further 'down' the length you go, until a limit is reached (about a lightyear from the origin in this case) at the event horizon (called the Rindler horizon). — noAxioms
Can you unpack this? The Rindler horizon can be reached one of two ways. As the worldline of a body undergoing acceleration, it is reached as that acceleration becomes infinite. This is the light-line (e.g. photon creation). As the proper time of a body undergoing proper acceleration, it is reached at eternity.
Why is your apparently infinitely long ship accelerating more the further away from x=0 you go? And why do you think it is infinitely accelerating one LY from x=0? -
 noAxioms
1.7k
noAxioms
1.7k
Not sure what worldlines have to do with this. Yes, the (constant) proper distance to the Rindler horizon of a small object undergoing continuous proper acceleration is a function of the magnitude of that acceleration. An extended object such as I described doesn't have a worldline so much as a 'world-swath' of sorts (the accelerated coordinate system of which I spoke) since each part of the object traces different worldlines, none of which intersect the worldlines of other parts.The Rindler horizon can be reached one of two ways. As the worldline of a body undergoing acceleration, it is reached as that acceleration becomes infinite. — Kenosha Kid
Sorry, I'm unfamiliar with that term. Google was no help.This is the light-line (e.g. photon creation).
Acceleration must be greater further 'down'. Less in the 'up' direction, so the 'ship' can be as long in that direction as required to serve its purpose as a coordinate system for an accelerated reference frame. It is somewhat equivalent to my weight being greater on the ground floor of a building than it is at a higher floor. Clocks run faster in the higher low-acceleration portions of the object than the clocks in higher-acceleration locations further down.Why is your apparently infinitely long ship accelerating more the further away from x=0 you go?
The product of the distance to the horizon and the inverse acceleration will equal c^2. So c^2 / 9.8m/sec^2 = ~9.2e15 meters which is not quite a light year.And why do you think it is infinitely accelerating one LY from x=0? -
 Kenosha Kid
3.2kNot sure what worldlines have to do with this. — noAxioms
Kenosha Kid
3.2kNot sure what worldlines have to do with this. — noAxioms
You brought up Rindler coordinates. There are two interpretations of these. The original is that they map the hyperbolic worldlines of accelerating bodies in an inertial frame. The second is that they map the length contraction of accelerating bodies in the bodies' non-inertial frames.
In the former, the Rindler horizon is the Minkowski worldline of a body with infinite acceleration, making it light-like, whereas in the latter it is the coordinate approached by an accelerating body as t goes to infinity. Either way, it's not something you can reach in a finite amount of time and with a finite amount of acceleration.
Yes, the (constant) proper distance to the Rindler horizon of a small object undergoing continuous proper acceleration is a function of the magnitude of that acceleration. — noAxioms
Actually it isn't. All accelerations lead to the horizon at eternity. None reach it in real time except, as said, infinite accelerations. How quickly they approach the horizon does depend on the acceleration, yes: x = 1/a.
Acceleration must be greater further 'down'. Less in the 'up' direction, so the 'ship' can be as long in that direction as required to serve its purpose as a coordinate system for an accelerated reference frame. — noAxioms
Nope, still not getting you. The only thing I can think is that this is a ship that is linear after Rindler transformation, i.e. that the coordinate x here is 1/a. Is that what you mean? I don't think this proves anything. It's effectively saying that after an eternity of travelling along the ship, the bit of the ship you're at will have reached its maximum acceleration and be at the horizon. Anything beyond that is unreachable purely from the fact that you can't reach, let alone pass, eternity. But that's just because your coordinate means the inverse of acceleration, not an actual event in spacetime. -
 noAxioms
1.7k
noAxioms
1.7k
What?? The body is accelerating away from the Rindler horizon. It's not approaching it. That's why I call the direction of it 'down'.in the latter it is the coordinate approached by an accelerating body as t goes to infinity. — Kenosha Kid
Thus I don't know what you mean by the wording here:
You have links where this wording is used? I'm trying to make sense of it.All accelerations lead to the horizon at eternity. -
 Kenosha Kid
3.2kWhat?? The body is accelerating away from the Rindler horizon. It's not approaching it. That's why I call the direction of it 'down'. — noAxioms
Kenosha Kid
3.2kWhat?? The body is accelerating away from the Rindler horizon. It's not approaching it. That's why I call the direction of it 'down'. — noAxioms
You cannot, by definition, "accelerate away from the Rindler horizon". That horizon is an acceleration limit. Lemme dig out a pic to explain.
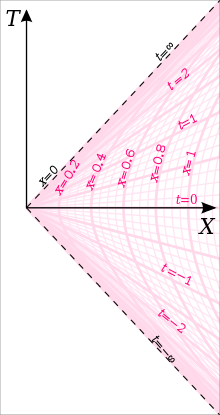
X here is position, T time in a Minkowski frame. The hyperbola are worldlines of bodies undergoing constant proper acceleration. t here is the proper time of the accelerating body.
As the body is accelerated for longer and longer, T and t increase. At infinity, all worldlines converge at the Rindler horizon, i.e. they have maximal velocity and converge to the worldline of infinite acceleration (the light-line).
So it's difficult to make sense of what you're saying. I get that you're trying to simulate gravity here. If you have a long ship pointed radially outward from a black hole, the bottom undergoes more acceleration than the top. I can't envisage, in the absence of gravity, how you can make a single object do the same. Perhaps a fleet of ships would be better. Non-rigid bodies were among the original hypothetical objects of the equivalence principle for this very reason. -
 noAxioms
1.7k
noAxioms
1.7k
Nonsense. Show me the definition that says this.You cannot, by definition, "accelerate away from the Rindler horizon". — Kenosha Kid
It is not. It, like any other event horizon, is a boundary in spacetime separating events that can have a causal effect on a given worldline and those events that cannot. So there is an event horizon currently about 16 billion light years distant beyond which no event can ever have a causal effect on Earth (the worldline in question here). This is due to the acceleration of Earth away from locations more distant than that. The only reason that is technically not a Rindler horizon is that Earth's acceleration is not constant, but is instead increasing.That horizon is an acceleration limit.
Lemme dig out a pic to explain.
And you choose a picture correctly showing the worldline of our observer at X=1 (assuming we choose units where α is 1), curving to the right (positive acceleration AWAY from the Rindler horizon to the left at X=0. The text accurately says "If the observer is located at time T = 0 at position X = 1/α (with α as the constant proper acceleration measured by a comoving accelerometer), then the hyperbolic coordinates are often called Rindler coordinates with the corresponding Rindler metric."
X = 1/α (a positive location). α is positive, so acceleration is away from location X=0 where the Rindler horizon is. Your post contradicts your own assertions.
The picture depicts the Rindler coordinates of one body, one worldline. Yes, other bodies to the left and right, at different accelerations, would trace those other worldlines, but their times would not correspond to the times plotted for the one object at X = proper distance of 1. The t= values are for that body and are not shown for any of the other worldlines.X here is position, T time in a Minkowski frame. The hyperbola are worldlines of bodies undergoing constant proper acceleration. t here is the proper time of the accelerating body.
After any amount of time, the proper distance between our accelerating body and the Rindler horizon remains 1. It is a constant. Sure, if you choose an inertial frame where this whole setup is moving fast, you can length contract it down to any size you like, but you don't need to wait a long time for that. Just choose a different frame. From the perspective of our constantly accelerating observer, the horizon remains at a fixed distance behind him (in the direction opposite his acceleration vector).As the body is accelerated for longer and longer, T and t increase. At infinity, they converge at the event horizon
You are unaware of acceleration not being constant along the length of an accelerating rigid object? This is a simple consequence of special relativity. Read up on Bell's paradox (the two ships accelerating while attached by string). It illustrates most of the concepts involved.So it's difficult to make sense of what you're saying. I get that you're trying to simulate gravity here. If you have a long ship pointed radially outward from a black hole, the bottom undergoes more acceleration than the top. I can't envisage, in the absence of gravity, how you can make a single object do the same.
And connect them with string, yes. Unfortunately, the clock of only one of those ships will correspond to the times depicted in the picture above.Perhaps a fleet of ships would be better. Non-rigid bodies were among the original hypothetical objects of the equivalence principle for this very reason. -
 Kenosha Kid
3.2kAnd you choose a picture correctly showing the worldline of our observer at X=1 (assuming we choose units where α is 1), curving to the right (positive acceleration AWAY from the Rindler horizon to the left at X=0. — noAxioms
Kenosha Kid
3.2kAnd you choose a picture correctly showing the worldline of our observer at X=1 (assuming we choose units where α is 1), curving to the right (positive acceleration AWAY from the Rindler horizon to the left at X=0. — noAxioms
Follow that worldline to the edge of the diagram. Now, tell me, is it closer to the horizon or further away? Yes, the worldline is bending to the right (increasing X). But the horizon is always moving to the right more quickly, except at eternity where all worldlines are parallel. Glad you see the relevance of worldlines now though.
acceleration is away from location X=0 where the Rindler horizon is. Your post contradicts your own assertions. — noAxioms
The Rindler horizon is not X=0. X=0 lies on the horizon at T=0.
You are unaware of acceleration not being constant along the length of an accelerating rigid object? This is a simple consequence of special relativity. Read up on Bell's paradox (the two ships accelerating while attached by string). It illustrates most of the concepts involved. — noAxioms
So what you mean is that we choose a frame of reference where the acceleration is not simultaneous Fine. That was the clarity I was seeking.
Your interpretation is still erroneous though, because you still think the Rindler horizon is a spatial horizon. It is not: it is a velocity limit that in turn limits how quickly and how much a body can accelerate (a rapidity limit). The length of the ship may for all intents and purposes be infinite in the origin's rest frame. As you move to more rapid parts of the ship through one part's frame of reference, you approach but never reach the rapidity of photon emission. And each successive part of the ship is length contracted with respect to the previous, so your ship beyond the origin fits in the space between X=0 and X=1 in that frame. The extent to which this is nuts is the extent to which an infinitely long ship undergoing acceleration is nuts.
This isn't different from what you started out with which my first response treated. Everything west of the Rindler horizon lies outside of the light cone of the part of the ship at the origin in its rest frame. You cannot map out an entire Minkowski space from the light cone of one event. That's fine because that's not what a Minkowski space is: it is a frame of reference containing all events, not just one. -
 noAxioms
1.7k
noAxioms
1.7k
The accelerating observer goes off the right side at about t=1.25, where proper distance to the horizon is still exactly x=1 behind him, unchanged. In another frame, the ship is moving, so of course the distance is length contracted, which would be true if the thing was accelerating or not. As I said, you don't need to wait for it's speed to change. Just do a Lorentz transform to a different arbitrary frame and you can contract that distance as much as you like, even at T=0.Follow that worldline to the edge of the diagram. Now, tell me, is it closer to the horizon or further away? — Kenosha Kid
Only in a frame different than the ship frame. That frame is thus arbitrary, and irrelevant to our observer's measure of the distance to the event horizon.Yes, the worldline is bending to the right (increasing X). But the horizon is always moving to the right more quickly
Yes, I acknowledge that in a different frame, that distance is contracted. This seems to be your point,.
It is a singularity, so this does not follow. Suppose the ship extends all the way back to the horizon. Where is the rear of the ship at t=1 (as measured by our observer at x=1)? Follow the t=1 line-of-simultaneity back to x=0 in the diagram. Where does it go? It goes to the same event where it was at t=0, the left-most event in the picture. That shows which event is approached as you move backwards in the accelerating frame. The actual event there is a singularity, with undefined time, so asking which horizon event is simultaneous with our observer at t=1.25 is meaningless, but I can point to the event in your arbitrary Minkowski frame that is approached.The Rindler horizon is not X=0. X=0 lies on the horizon at T=0.
Unclear what you mean by this. Acceleration is continuous, not something that is 'simultaneous'. At all times in ship frame, all parts of the ship are moving at the exact same speed, and thus the entire ship is always stationary in its own accelerating frame. The ship is said to be Born-rigid.So what you mean is that we choose a frame of reference where the acceleration is not simultaneous
This implies that in a different frame (such as the Minkowski one in the pic), the various parts of the ship are not moving at the same speed. If they did, length contraction would contradict it, as shown by Bell's 'paradox'.
I don't 'think' that. It is a coordinate singularity, just like the one 16 billion light years away, and just like the event horizon of a black hole. The center of a black hole on the other hand is an example of a physical singularity. A coordinate singularity only exists in certain coordinate systems, and there's nothing actually physically weird going on at them. Hence people can drop into a sufficiently large black hole without really noticing any obvious immediate change, not even if they're looking out of the window. A small one of course will kill you before you get there.Your interpretation is still erroneous though, because you still think the Rindler horizon is a spatial horizon.
Only to the right in this case, not the left. Can't go past x=0. For the same reason, I cannot have a rigid rod much longer than about 27BLY with us stationary at the midpoint. It is an interesting exercise to figure out how to position a rod of twice that length without strain. It can be done. I digress.The length of the ship may for all intents and purposes be infinite in the origin's rest frame.
I assume 'more rapid' means higher acceleration (and associated rate of change in rapidity) and not high-speed since the ship is always stationary along its entire length in its own frame (the frame in which rapidity is meaningful), so there is no different frame of reference between one part and another. There is a variable rapidity change rate that is dependent on the different parts of the ship. Over at x=1, acceleration is 1, so the rapidity there is a function of how long it's been doing that between two times as measured by a clock there. At higher acceleration parts of the ship, the same time interval results in a greater rapidity change over the same interval on again a local clock. The rapidity of light is infinite, but I don't know what 'rapidity of photon emission' means.As you move to more rapid parts of the ship through one part's frame of reference, you approach but never reach the rapidity of photon emission
It contains all events in the Minkowski frame, but in real spacetime, light should be able to get here from far away given enough time, but it doesn't in reality, so the Minkowski model fails to describe the large-scale structure of our universe. It is, and always has been, a model of local spacetime.You cannot map out an entire Minkowski space from the light cone of one event. That's fine because that's not what a Minkowski space is: it is a frame of reference containing all events, not just one. -
 Kenosha Kid
3.2kI don't 'think' that. It is a coordinate singularity, just like the one 16 billion light years away, and just like the event horizon of a black hole. — noAxioms
Kenosha Kid
3.2kI don't 'think' that. It is a coordinate singularity, just like the one 16 billion light years away, and just like the event horizon of a black hole. — noAxioms
I have found this page: https://www.gregegan.net/SCIENCE/Rindler/RindlerHorizon.html and wondered if this or something like this is where you've gotten your impression (it talks about spaceships and Rindler horizons). Note the following:

the dashed line in the figure above shows the world line of a flash of light emitted from x=0 at t=0
...
the dashed line constitutes a kind of event horizon, known as the Rindler horizon
If the above is indeed your source, I hope this convinces you that it is the entire x=0 (or t=infinity) line that is the Rindler horizon, not the X=x=0 point. Next:
Of course, this is not the same as a black hole’s event horizon in two very important respects. Firstly, it’s always possible to stop the spaceship accelerating, so this horizon’s persistence is a matter of choice, not physical law. Secondly, there is nothing corresponding to a black hole’s singularity to do any actual damage to anything passing through the horizon.
This is not a real event horizon like the boundary of the universe or that of a black hole. It is an artificial horizon based on the decision of the ship to constantly accelerate away from everything else. Things effectively cannot reach it (cannot reach x=0) because it moves away from them. However, things can get closer to it (move toward x=0) in its own proper frame. It still has a negative x-direction, and there is no singularity.
Because lightspeed is not observer-independent in non-intertial frames (trivial example: a rotating observer), while it cannot have zero speed, it can have a speed between 0 and c for an observer moving away from it. You seem to think this makes a profound statement about the space behind the accelerating observer, but it doesn't. It is equivalent, in inertial motion, to saying that an object that is following me with the same speed as me doesn't reach me. Or, in my rest frame, a static object to my left is not occupying the same coordinate as me.
The photon is still in the moving observer's coordinate system, it is just always in the negative x positive t quadrant. It isn't the case that space outside the moving observer's light cone is not inside their coordinate system. In other words, you can still create the Minkowski frame from a foliation of the accelerating observer's proper frame, it's just that you have a time-dependent length-contraction to deal with instead of a constant one. A black hole, on the other hand, is a worldline in the Minkowski frame that is genuinely inaccessible to the freefalling observer, i.e. it only exists as an event in the freefalling body's proper frame at eternity. -
 noAxioms
1.7k
noAxioms
1.7k
That's the same as the wiki picture, but with far less detail. Yes, in an arbitrary inertial reference frame as depicted in all these drawings, that entire line is the Rindler horizon. Under Rindler coordinate time (not shown in this new picture), the horizon is a coordinate singularity and is not comprised of a line like that. Time is infinitely dilated, and there is no light cone if there is zero time for light to get anywhere.If the above is indeed your source, I hope this convinces you that it is the entire x=0 (or t=infinity) line that is the Rindler horizon, not the X=x=0 point. — Kenosha Kid
Similarly, you can accelerate away from Earth to push the distant event horizon further away in the coordinate space of the thing accelerating away, but that just pushes it off. You can't turn off the acceleration of expansion like you can turn off the ship engine. Yes, I agree, the Rindler horizon exists for a continuously accelerating thing, and it ceases to exist when that condition goes away.Of course, this is not the same as a black hole’s event horizon in two very important respects. Firstly, it’s always possible to stop the spaceship accelerating
Nothing is inherently damaged by free-falling through a black hole event horizon. Are you under the impression otherwise? As I said, a small black hole will 'damage' you before you even get to the event horizon, but that's not the event horizon doing it to you. Orbit close enough to a neutron star and you're dead, no event horizon needed at all.Secondly, there is nothing corresponding to a black hole’s singularity to do any actual damage to anything passing through the horizon.
I was unaware of there being a boundary of the universe. In the ship case, yes, you have the option of turning off the acceleration. In the dark energy case, you do not, so no matter what you choose to do, there are points in space in no significant gravity well from which light can never reach you. This is not true in Minkowski spacetime.This is not a real event horizon like the boundary of the universe or that of a black hole.
No. My bold. This is where you're wrong. Nothing can ever get closer to it in its own proper frame. That's what I've been repeating in the last several posts.It is an artificial horizon based on the decision of the ship to constantly accelerate away from everything else. Things effectively cannot reach it (cannot reach x=0) because it moves away from them. However, things can get closer to it (move toward x=0) in its own proper frame.
Maybe you could address my points instead of just repeating your own. The wiki picture shows the proper frames of the accelerating object, and since the picture is a different frame, it actually shows the distance increasing, but in the Rindler coordinates, the distance is constant over time. If it wasn't, there would be a test for absolute rest: when the distance to the rear of the ship is at a maximum. That would be a direct violation of Galilean relativity, the first of the SR postulates.
No argument.Because lightspeed is not observer-independent in non-intertial frames
Do you accept that the accelerating object is always stationary in its own frame? I know it's not an inertial frame, but if you take any event on the ship (say the pilot at x=1 at time t=2, his clock), and you reference the one inertial frame in which the pilot is momentarily stationary at that event, then every location along the ship is simultaneously (relative to that IRF) stationary. In that frame, the Rindler horizon is still a distance of 1 behind the pilot, regardless of the time that has passed.It is equivalent, in inertial motion, to saying that an object that is following me with the same speed as me doesn't reach me. Or, in my rest frame, an object to my left is not occupying the same space as me.
I typically imagine a ship of length almost 2 with the pilot in the middle and the rear just shy of the Rindler horizon, and the front at x=2.
Not the one at the rear. Time is stopped there in that coordinate system, and the photon makes no better progress than one at a black hole horizon trying to get out. A photon anywhere forward of that does indeed make progress and will eventually reach any part of the ship.The photon is still in the moving observer's coordinate system -
 Kenosha Kid
3.2kTime is infinitely dilated, and there is no light cone if there is zero time for light to get anywhere.
Kenosha Kid
3.2kTime is infinitely dilated, and there is no light cone if there is zero time for light to get anywhere.
...
Nothing can ever get closer to it in its own proper frame. That's what I've been repeating in the last several posts. — noAxioms
Yes, I know. And this is why your argument is incorrect. You seem to think that somehow, in the accelerating observer's frame, the distance from x=0 to x>0 is infinite in the proper frame because nothing from x<0 can reach x=0, akin to saying that if two cars were travelling in the same direction at the same speed, the car behind can't be represented in the rest frame of the car in front because it cannot reach it.
This is quite incorrect except, as I've mentioned several times, when the accelerating body reaches a velocity of c, which it cannot. For all finite accelerations within finite times, there is no infinite time dilation, no infinite length contraction, and any light approaching from the negative x-direction is getting closer, even if it cannot intersect the accelerating body's worldline in finite time. None of this is new: you can do all of the math in standard SR.
Do you accept that the accelerating object is always stationary in its own frame? — noAxioms
If you'd read me carefully, I not only accept it, I asserted it. This is all x=0 is in the rest frame of the moving body: a coordinate of the origin of that frame. It is not a singularity by any definition.
Maybe you could address my points instead of just repeating your own. — noAxioms
The problem is you don't understand the framework you're trying to use to make your point, so don't understand why your point is invalid. I can't address your points in the way you'd like because your conception of Rindler coordinates is wrong, not just incidentally but fundamentally. I am trying to explain what any book on non-inertial motion will explain and frankly I would rather you'd just read one because I do appreciate that you're not going to take correction from a randomer on the internet claiming to be a former relativity lecturer. You have to do the legwork, not just try and jump to the crazy conclusions of some impossible edge cases and mistake that for the theory as a whole. -
 noAxioms
1.7k
noAxioms
1.7k
I do not think this any more than I think the distance to a black hole EH is infinite because light from it will never reach an orbiting object. Pilot at x=1, RH at x=0. That's a constant finite distance of 1 (as I've said above), not an infinite distance as you suggest here.[At location x=0 in the ARF,] Time is infinitely dilated, and there is no light cone if there is zero time for light to get anywhere.
...
Nothing can ever get closer to it in its own proper frame. That's what I've been repeating in the last several posts.
— noAxioms
Yes, I know. And this is why your argument is incorrect. You seem to think that somehow, in the accelerating observer's frame, the distance from x=0 to x>0 is infinite in the proper frame because nothing from x<0 can reach x=0 — Kenosha Kid
I never said one car cannot be represented in the frame of the other. That's partly because they're the same car, the front and rear bumper, moving by definition at the same speed in the rigid car's own frame. But the rear bumper must accelerate harder than the front one. The car on the other side of the RH is what cannot be represented in the Rindler frame of the accelerating car. It cannot be keeping up with the accelerating (but stationary) car in the ARF. (Please tell me if any of these acronyms are confusing. I tire of typing the full words).akin to saying that if two cars were travelling in the same direction at the same speed, the car behind can't be represented in the rest frame of the car in front because it cannot reach it.
Yes, and the math says the acceleration cannot be finite at the RH, and which is why I said the length of my object extended almost 1 to the rear, but not all the way, because I wanted to avoid the infinite acceleration required there, with yes, infinite time dilation, just like at the EH of a black hole.For all finite accelerations within finite times, there is no infinite time dilation, no infinite length contraction, and any light approaching from the negative x-direction is getting closer, even if it cannot intersect the accelerating body's worldline in finite time. None of this is new: you can do all of the math in standard SR.
Good. I wasn't sure given your posts.Do you accept that the accelerating object is always stationary in its own frame?
— noAxioms
If you'd read me carefully, I not only accept it, I asserted it.
In the Minkowski frame, we know where the x=0 point is at t=0. It is at X=0, T=0, right? Think wiki picture if you don't know what I mean. Our object extends from X=2 back to X=0. It is effectively a long meter-stick in a rail gun, with a clock at each end and in the middle.This is all x=0 is in the rest frame of the moving body: a coordinate of the origin of that frame. It is not a singularity by any definition.
t is what's on the middle clock at the accelerating object at x=1. So at t=2, that clock is off the right side of the picture, but not far. Suppose we stop accelerating the entire object simultaneously (in the object frame) when that clock reads t=2. Where is x=0 in the object's frame? I contend that despite infinite acceleration there, it has gone nowhere and is still at X=0, T=0 (in the original Minkowski coordinates, which is not the object's frame) and not anywhere else on that picture. The clock at the rear of the object still reads zero. Do you agree with any of this? If not, where (in the original Minkowski diagram) is the left end of the object (simultaneous with, in the object's new frame, the cessation of acceleration at t=2 on the middle clock?
You continue to make erroneous assumptions about what I'm saying, so of course you think I'm getting something wrong. No, I never claim a pair of cars following each other are not in each other's reference frames. You totally don't get my point if that's your take.The problem is you don't understand the framework you're trying to use to make your point, so don't understand why your point is invalid.
I'm asking you to do some legwork in the example above, to compute which event corresponds to the cessation of acceleration at the rear of the object, and where that event falls in the original Minkowski diagram. I can do the same mathematics if you like, but the picture already shows the event in question.You have to do the legwork, not just try and jump to the crazy conclusions of some impossible edge cases and mistake that for the theory as a whole.
You seem to have been claiming that the RH somehow approaches the x=1 point in the ARF as the object accelerates, but in the object's ARF, the object is always stationary, so that can't be happening. It must remain a constant distance from x=1. -
 Kenosha Kid
3.2kThe car on the other side of the RH is what cannot be represented in the Rindler frame of the accelerating car. It cannot be keeping up with the accelerating (but stationary) car in the ARF. (Please tell me if any of these acronyms are confusing. I tire of typing the full words). — noAxioms
Kenosha Kid
3.2kThe car on the other side of the RH is what cannot be represented in the Rindler frame of the accelerating car. It cannot be keeping up with the accelerating (but stationary) car in the ARF. (Please tell me if any of these acronyms are confusing. I tire of typing the full words). — noAxioms
The Rindler horizon's similarity to the event horizon is only insofar as any light travelling from the negative x direction cannot reach the x=0 worldline. That seems to be the entire basis for your argument that the space the photon travels in does not exist in the Rindler frame. This is exactly the same as saying the car behind does not exist in the frame of the car in front because it can never reach it. It's the same argument.
Yes, and the math says the acceleration cannot be finite at the RH — noAxioms
Except for the x=0 (light-like) worldline, yes. But...
which is why I said the length of my object extended almost 1 to the rear, but not all the way, because I wanted to avoid the infinite acceleration required there, with yes, infinite time dilation, just like at the EH of a black hole. — noAxioms
But you don't have to do this. If the acceleration of the leftmost part of the ship is finite at T=t=0, it will not follow the x=0 worldline (the light-line) but one of the x>0 ones. Infinite acceleration is the only way to follow the x=0 worldline. The leftmost end and rightmost end will not have the same horizon in the Minkowski frame, i.e. the horizon is proper-frame--dependent.

Two observers having the same proper acceleration (Bell's spaceships). They are not at rest in the same Rindler frame, and therefore have different Rindler horizons — https://en.wikipedia.org/wiki/Bell%27s_spaceship_paradox
(I am thinking of changing my username to BornRigid but I might get banned.)
As per Bell's paradox, there exists an inertial frame of reference in which we can arrange for the acceleration of the ship to be the same at both ends. As per Wiki:
Consider two identically constructed rockets at rest in an inertial frame S. Let them face the same direction and be situated one behind the other. If we suppose that at a prearranged time both rockets are simultaneously (with respect to S) fired up, then their velocities with respect to S are always equal throughout the remainder of the experiment (even though they are functions of time). This means, by definition, that with respect to S the distance between the two rockets does not change even when they speed up to relativistic velocities. — https://en.wikipedia.org/wiki/Bell%27s_spaceship_paradox

This ship would break apart because each section of it would be length contracted while maintaining its distance from the adjacent section, but the take-home of this is that it doesn't matter where the two ends are. One can always construct another inertial frame at rest wrt the first in which either end is zero or both non-zero. There is nothing special about the initial coordinate of each end of the ship because each end has its own Rindler horizon in its proper frame.
When we choose one of the proper frames, the worldlines of each end will be constrained by the Rindler horizon of the proper frame we choose (either to stay to the right or to the left of it depending on whether the initial position of the other end is to the left or the right of the light-line. Let's take the rightmost end as the proper frame. In its frame, it is not moving, and the left end is moving away from it. To see this, refer again to:

choose the point on the worldline to the right where t=1, and follow the t=1 line back to the other end of the ship. If the leftmost ship is still at x=0 (because it started at X=0), it is still at T=0 in the Minkowski frame, and its velocity is therefore zero: no length contraction occurs at the leftmost end because it is not yet moving. (Length contraction is a function of velocity, not acceleration.)
This ship would break apart in the proper frame of the rightmost end because parts to the left are moving away from the rightmost part with increasing acceleration. The leftmost part's coordinate still exists in the rightmost part's proper frame (indeed, we just traced to that coordinate with our finger).
As I said before, if the length of the ship in the proper frame of the rightmost part is infinite and the leftmost part is at X=x=0 at T=t=0 and the rightmost part has a finite X at some time T, then yes, in the Minkowski frame there will be infinite length contraction fitting the infinite length of the ship into the finite length between the x=0 worldline and X, because in the proper frame of the rightmost part of the ship (at infinity), the leftmost part of the ship is receding away at infinite acceleration. But since this is a physical impossibility, don't worry about it. For all finite lengths, the length contraction is zero or finite everywhere except at t=infinity. -
 noAxioms
1.7kBeen too busy to deal with this fairly unproductive line of discussion.
noAxioms
1.7kBeen too busy to deal with this fairly unproductive line of discussion.
What light can or cannot do is irrelevant to my point. It is similar in other ways, which is why I brought it up. My arguments have not been based on light signals.The Rindler horizon's similarity to the event horizon is only insofar as any light travelling from the negative x direction cannot reach the x=0 worldline. That seems to be the entire basis for your argument that the space the photon travels in does not exist in the Rindler frame. — Kenosha Kid
Either car can say what the other is doing 'now', whether they can reach each other or not, so it is not the same at all. You continue to either not get my point, or you're deliberately evading it because its implications make you uncomfortable. So address the question I asked and not another:This is exactly the same as saying the car behind does not exist in the frame of the car in front because it can never reach it. It's the same argument.
A clock is dropped at Rindler event T=0 X=1. What are the Rindler coordinates of that clock when it reads T=1? When it reads T=2?
That's the question. There's no mention of light in it. I claim a lack of coherent answer, and conclude that Rindler coordinates are inadequate to the task of foliating all of spacetime. Similarly, inertial coordinates cannot foliate spacetime containing a black hole, and no coordinate system can foliate spacetime containing multiple black holes. -
 Kenosha Kid
3.2kWhat light can or cannot do is irrelevant to my point. It is similar in other ways, which is why I brought it up. My arguments have not been based on light signals. — noAxioms
Kenosha Kid
3.2kWhat light can or cannot do is irrelevant to my point. It is similar in other ways, which is why I brought it up. My arguments have not been based on light signals. — noAxioms
You cannot talk of length-contraction and hold that what light can or cannot do is irrelevant. That makes absolutely no sense. Relativity is fundamentally tied to the behaviour of light in different frames. Remove that, and you lose the Lorentz transformations. Remove the Lorentz transformations and you lose length contraction. Lose that, and you have no Rindler coordinate system. As tempting as it is for the lay person to jump in at the most fascinating stuff, you have to know the relevant foundations, otherwise you find yourself saying things like the above. Sorry, that's just the way it is. -
 noAxioms
1.7kI know it has been two years, but I am retracting my 'proof'.
noAxioms
1.7kI know it has been two years, but I am retracting my 'proof'.
I have become aware of the fairly recent Schmelzer model, a generalization of Lorentz Ether Theory, that posits a preferred frame for all events, something I said could not be done for 'all events',
It recognizes the inconsistencies I've pointed out, and solves the unordered event problem by denying the existence of the events in question. There are no black holes, only 'frozen stars' with no interior (not even empty space). Infalling observers subjectively die at the event horizon. The big bang also contradicts presentism, and the theory gets around it by positing a big bounce. There is no beginning and no something-from-nothing problem inherent in presentism.
This of course leads to a similar empirical test as there is for an afterlife. You can validate the model, but you can't report the results back to home. Jump into a black hole. If you cross the event horizon without anything noticeably changing, then Einstein's block universe is right and the preferred foliation model is bunk. If you die there, Einstein was wrong. Either way, no paper gets published in a journal.
Welcome to The Philosophy Forum!
Get involved in philosophical discussions about knowledge, truth, language, consciousness, science, politics, religion, logic and mathematics, art, history, and lots more. No ads, no clutter, and very little agreement — just fascinating conversations.
Categories
- Guest category
- Phil. Writing Challenge - June 2025
- The Lounge
- General Philosophy
- Metaphysics & Epistemology
- Philosophy of Mind
- Ethics
- Political Philosophy
- Philosophy of Art
- Logic & Philosophy of Mathematics
- Philosophy of Religion
- Philosophy of Science
- Philosophy of Language
- Interesting Stuff
- Politics and Current Affairs
- Humanities and Social Sciences
- Science and Technology
- Non-English Discussion
- German Discussion
- Spanish Discussion
- Learning Centre
- Resources
- Books and Papers
- Reading groups
- Questions
- Guest Speakers
- David Pearce
- Massimo Pigliucci
- Debates
- Debate Proposals
- Debate Discussion
- Feedback
- Article submissions
- About TPF
- Help
More Discussions
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum


