-
 Metaphysician Undercover
14.9kYou can talk about infinities all you want to. But you cannot produce one. For you to produce something that would go on forever, you yourself would have to live forever to do it. That's the whole point. — h060tu
Metaphysician Undercover
14.9kYou can talk about infinities all you want to. But you cannot produce one. For you to produce something that would go on forever, you yourself would have to live forever to do it. That's the whole point. — h060tu
All you need to do is define "infinity" in such a way that you can produce them, and voila, you can produce infinities. It's a very simple trick which the mathemagicians do with their axioms. However, we need to respect the fact that when they talk about infinities they are not talking about the same thing as you, when you talk about infinity. -
 Metaphysician Undercover
14.9kThat is why, in my first reply on this thread I described two very distinct ways of using "1", to expose the ambiguity in mathematical terms, hoping to reveal the fact that ambiguity and equivocation are abundant in mathematics: https://thephilosophyforum.com/discussion/comment/404312
Metaphysician Undercover
14.9kThat is why, in my first reply on this thread I described two very distinct ways of using "1", to expose the ambiguity in mathematical terms, hoping to reveal the fact that ambiguity and equivocation are abundant in mathematics: https://thephilosophyforum.com/discussion/comment/404312 -
 Harry Hindu
5.9k
Harry Hindu
5.9k
Then 1 does refer to things, like velocity and time. Glad to see that you finally see that I made sense, Banno.We agree that an object has a location at a particular time.
We agree that the location does not change at an instant.
Where we disagree is that there are those amongst us who are happy to ascribe a velocity at a particular time, and those who are not.
What is hard to see is how those who do not ascribe a velocity at a particular time can do any basic mechanics.
It's the 0.9999... = 1 denialists, hard at work again. — Banno
Now, the question is, does speed and time exist as something other than a concept, or as a potential, not an actual, like infinity?
What is an instant? Think about what an instant looks like to you and then what an instant looks like to a cold-blooded lethargic lizard. That cat is moving at a relative speed (velocity) of 15 mph to your eyes, but to the lizard, it's movement was instantaneous.
In talking about velocity, we are talking about the relationship between a certain change in location relative to something else during a certain time. Velocity in miles per hour is how many miles (the relative) something moved during one hour.
Now, if the lethargic lizard could measure velocity, while the velocity of the cat would be instantaneous to the lizard and take time to you, the change in location of the cat relative to the length of a mile will still be proportionally the same. So while our perspectives of time and velocity may be different, the proportional relationships stay the same. -
 ztaziz
911. You place a set of 40 different Pokemon Cards on a table in some order, labelled 1-40.
ztaziz
911. You place a set of 40 different Pokemon Cards on a table in some order, labelled 1-40.
2. You divide the set by 1, equating 40 for Y.
3. Order is lost in simple division, treating all different cards as label 1.
4. Repeat step 1.
5. You divide the set by 2, equating 20 for X.
6. Order is implied for X has 20 specific cards out of 40.
7. Order is implied for Y.
8. 1 is not powerful enough a number.
2/40 can be a number of different cuts; at step 6 there are many possible sets of cards in X's control, and thus 2/40 = 20 is wrong; overly simple. You can try the same method with all labelled 1, and get the same result. There is an error at step 2.
40 cards are not the same as 40 1s. 1s seem to blend, per se, to make 2. No matter what, if you have 2 cards. That's card 1 and card 2, never a single card
So 1 + 1 does not equal 2, but rather (1 1), which can be said to be 2, but, following on from 2, is stupid, it's just a reference to (1 1), follow on from (1 1).
End. -
 h060tu
120All you need to do is define "infinity" in such a way that you can produce them, and voila, you can produce infinities. It's a very simple trick which the mathemagicians do with their axioms. — Metaphysician Undercover
h060tu
120All you need to do is define "infinity" in such a way that you can produce them, and voila, you can produce infinities. It's a very simple trick which the mathemagicians do with their axioms. — Metaphysician Undercover
No. You can model a system that produces infinities. But you cannot actually create an abstract thing that is infinite. That's a different thing. I mean technically, replaying a video game each time will produce an infinite number of different conditions in the game, being different each time. The game isn't infinite. That's the system that is modeling infinity, not the actual thing. Simulation vs simulator. Not the same thing. I keep having to repeat this difference. -
 jgill
4khoping to reveal the fact that ambiguity and equivocation are abundant in mathematics — Metaphysician Undercover
jgill
4khoping to reveal the fact that ambiguity and equivocation are abundant in mathematics — Metaphysician Undercover
I'll take that under consideration since you obviously have an in-depth knowledge of the subject. :roll: -
 ztaziz
911. I'm playing a video game.
ztaziz
911. I'm playing a video game.
2. There is a refill ammo box.
3. I place a camera on a wall, and then refill ammo and continue to place cameras.
4. I can do this until: the game is impossible to play, there is no space for cameras or I destroy the ammo box.
A model of infinity is impossible, but not an infinite practice.
The walls fill up, the game costs, requiring that I put in effort to run the program infinitely. Riding a eco cycle to supply energy to my console, removing and replacing cameras on a wall, and THEN I could go on infinitely; however, it's a different infinity than the original. I'm not, 'infinitely placing the cameras', I'm infinitely replacing cameras (which means I need to place X amount of cameras).
A great cog is required for any practice of infinity. -
 Metaphysician Undercover
14.9kI'll take that under consideration since you obviously have an in-depth knowledge of the subject. — jgill
Metaphysician Undercover
14.9kI'll take that under consideration since you obviously have an in-depth knowledge of the subject. — jgill
Yeah, I think we've met on some other threads with similar subjects. Now I think you're beginning to catch on. It's just a matter of analyzing the axioms, in order to understand what they actually mean. I would recommend this as a revealing practise for any philosopher. Mathematicians on the other hand seem to be disinterested, being more inclined to take the axioms for granted as if they are some sort of eternal truths. -
 jgill
4kMathematicians on the other hand seem to be disinterested, being more inclined to take the axioms for . . . — Metaphysician Undercover
jgill
4kMathematicians on the other hand seem to be disinterested, being more inclined to take the axioms for . . . — Metaphysician Undercover
Mathematics evolved over millennia and foundations are fairly recent. Most practicing mathematicians, especially those in classical mathematics, just do the math they are interested in and avoid arguments over the axioms that lie at the base of foundations. Of course, analytic philosophers, set theorists and other math people can be heavily involved in foundations, and keenly feel perturbations in that structure that would go unnoticed by the rest of us.
For me, arguments in transfinite mathematics seem far too abstract, but for others they may represent the soul of the subject. Personally, doing minor research in classical complex analysis I've never needed to go transfinite. But others in what is called modern or "soft" analysis have used debatable axioms like the Axiom of Choice for their investigative results.
If you are a person who feels strongly that the axiomatic structure of math contains flaws, the go for it. There's room for everyone. :cool: -
 Metaphysician Undercover
14.9kMathematics evolved over millennia and foundations are fairly recent. — jgill
Metaphysician Undercover
14.9kMathematics evolved over millennia and foundations are fairly recent. — jgill
You ought to recognize this as contradictory. The foundations are what something is built upon, and therefore cannot be something recent when the thing has been around for millennia. So this statement implies that you misunderstand what the foundations of mathematics really are, interpreting something recent as the foundations, when this really cannot be "the foundations" which must refer to what the thing is built on. Take a look at Banno's op, there is a reference to "counting", I suggest you'll find the foundations of mathematics here. But counting has two very distinct purposes, one is to determine a number of things, quantity, and the other is to determine an order of things, priority.
Because of these distinct purposes, we have ambiguity and the potential for equivocation right at the basic, most fundamental principles of mathematics. So "number one" refers to an individual, a particular, as distinct from others, for the purpose of counting, but it also refers to the first in terms of priority. With the introduction of zero, and negative integers, "one" has lost its status as the first, so we need other principles to understand the concept of priority. Where are these principles of priority? It appears like modern mathematics gives us no principles of order, having given priority (importance) to quantity at the cost of sacrificing order. The result, modern mathematics is a disorderly mess. -
 jgill
4kSo this statement implies that you misunderstand what the foundations of mathematics really are — Metaphysician Undercover
jgill
4kSo this statement implies that you misunderstand what the foundations of mathematics really are — Metaphysician Undercover
The result, modern mathematics is a disorderly mess. — Metaphysician Undercover
I know. It's a tragedy that requires competent philosophical guidance. Thanks for being there when we need you! :scream: -
 unenlightened
10kAnd yet, by the magic of non-referential communication and with years of training, Mrs un knows how many sugars I Like in my coffee. And if it is not too esoteric for your philosophy, you will reach the same understanding as soon as I confide that I like 1 teaspoonful. In this context, 1 serves as an instruction not to repeat an action.
unenlightened
10kAnd yet, by the magic of non-referential communication and with years of training, Mrs un knows how many sugars I Like in my coffee. And if it is not too esoteric for your philosophy, you will reach the same understanding as soon as I confide that I like 1 teaspoonful. In this context, 1 serves as an instruction not to repeat an action.
Wait, hang on. Does repeat refer?
"The" does not refer to anything. Is this a problem?
My physics teacher used to say 'a number means nothing until you state your units.'
The solution is that 'the' does not refer until you say "solution".
"1" does not refer. "1 sugar in my coffee" refers as much as anything because the units have been specified.
Hurrah for physics. -
 Metaphysician Undercover
14.9kI know. It's a tragedy that requires competent philosophical guidance. Thanks for being there when we need you! :scream: — jgill
Metaphysician Undercover
14.9kI know. It's a tragedy that requires competent philosophical guidance. Thanks for being there when we need you! :scream: — jgill
No, few people listen to any philosophers, and that's a tragedy in itself. So we have a double tragedy, philosophical guidance is needed, but it's not heeded. My existence is irrelevant. -
 jgill
4kSo we have a double tragedy, philosophical guidance is needed, but it's not heeded. — Metaphysician Undercover
jgill
4kSo we have a double tragedy, philosophical guidance is needed, but it's not heeded. — Metaphysician Undercover
This seems to be primarily an amateurs' forum - and I don't mean this in a pejorative way - in that few if any make their living as professional philosophers (probably requiring graduate degrees). Your ideas on the foundations of mathematics might receive a more serious scrutiny were you to post them on a site like https://www.google.com/search?client=firefox-b-1-d&q=math+stackexchange . Yoiu might find some there who would agree with you. Just a thought. :cool: -
 Deleted User
-15Your ideas on the foundations of mathematics might receive a more serious scrutiny were you to post them on a site like https://www.google.com/search?client=firefox-b-1-d&q=math+stackexchange . — jgill
Deleted User
-15Your ideas on the foundations of mathematics might receive a more serious scrutiny were you to post them on a site like https://www.google.com/search?client=firefox-b-1-d&q=math+stackexchange . — jgill
I wonder if you know of any good forums for psychology or sociology...Thanks! -
 Banno
30.6k
Banno
30.6k -
 EnPassant
725Positive integers can be generated by a process of iteration and partition:
EnPassant
725Positive integers can be generated by a process of iteration and partition:
Start with "/"
Iterate: //
And again: ///
And again: ////
So you get ///////////////////...
Partition each step: /, //, ///, ////,...
These partitions are sets
{/}, {//}, {///}, {////},...
and they are represented in Arabic numerals as
1, 2, 3, 4,...
The initial / need not be anything other than a concept of something or nothing.
In mathematics it can be the null set.
Counting infinity has nothing to do with time. An infinity of numbers does not require time to exist. They exist conceptually as a set. -
 jgill
4kCounting infinity has nothing to do with time. — EnPassant
jgill
4kCounting infinity has nothing to do with time. — EnPassant
In a sense. However, as a mathematical analyst, when I iterate w=f(z)=z+1, starting with z=1, the process is unbounded and hence is said to diverge to infinity. In a computer program each iterative step requires a tiny amount of time, so time is tied in with this notion of counting infinity, although in theory the pace is arbitrary. Is it possible to think of a process that counts to infinity and does not require a step-by-step procedural? Certainly the concept of the set of counting (natural) numbers as a theoretical entity is not tied to time. :chin: -
 Metaphysician Undercover
14.9kCounting infinity has nothing to do with time. An infinity of numbers does not require time to exist. — EnPassant
Metaphysician Undercover
14.9kCounting infinity has nothing to do with time. An infinity of numbers does not require time to exist. — EnPassant
It requires an infinity of time to count an infinity of numbers, so "counting infinity" does have something to do with time. -
 Banno
30.6k...time... — jgill
Banno
30.6k...time... — jgill
Hm. It requires a sequence, sure. But a sequence is not the same as time.
Consider a Koch Snowflake, which has a finite area yet an infinite perimeter...
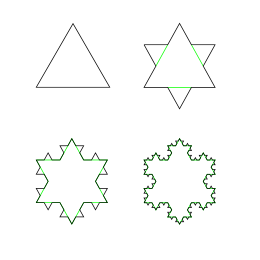
...and in considering it, one finds oneself as it were, standing outside of the iterative process that creates the flake; one understands the flake despite not having performed every iteration.
Unless ons is @Metaphysician Undercover. -
 A Seagull
615It requires an infinity of time to count an infinity of numbers, so "counting infinity" does have something to do with time. — Metaphysician Undercover
A Seagull
615It requires an infinity of time to count an infinity of numbers, so "counting infinity" does have something to do with time. — Metaphysician Undercover
You cannot count an infinity of numbers, so time has got nothing to do with it. -
 Metaphysician Undercover
14.9k
Metaphysician Undercover
14.9k
Counting is a temporal process. Two comes after one. Three comes after two. You cannot remove the temporal aspect of counting, to claim that time is irrelevant to counting. It is essential. Try counting when four comes before three. It doesn't work. -
 A Seagull
615Much of the problems of the foundations of mathematics are caused by the failure to distinguish between pure and applied maths, all too often the two are conflated as though there is some God-given connection between the two.
A Seagull
615Much of the problems of the foundations of mathematics are caused by the failure to distinguish between pure and applied maths, all too often the two are conflated as though there is some God-given connection between the two.
Other problems ar3e caused by considering that axioms and theorems are two distinct entities, when in fact one runs into the other. ie a theorem can be used as an axiom. or 2+2=4 can be considered to be axiomatic.
Also maths might be less confusing to philosophers if they stuck to numbers in base 1 instead of base 10. -
 A Seagull
615↪A Seagull
A Seagull
615↪A Seagull
Counting is a temporal process. Two comes after one. Three comes after two. You cannot remove the temporal aspect of counting, to claim that time is irrelevant to counting. It is essential. Try counting when four comes before three. It doesn't work. — Metaphysician Undercover
Pure maths is entirely abstract. You are conflating pure maths with applied maths. Numbers in pure maths do not require counting. -
 Metaphysician Undercover
14.9k
Metaphysician Undercover
14.9k -
 Marchesk
4.6kWhere do you think our sense of infinity comes from? It comes from us, i.e., finite beings, we create the concepts using finite signs. We extrapolate based on the continuation of 1,2,3.. that it goes on ad infinitum. There's no mystery here. — Sam26
Marchesk
4.6kWhere do you think our sense of infinity comes from? It comes from us, i.e., finite beings, we create the concepts using finite signs. We extrapolate based on the continuation of 1,2,3.. that it goes on ad infinitum. There's no mystery here. — Sam26
However, since nobody is constructing the sequence ad infinitum, it can't be said to go on forever. So the question becomes how a constructionist can justify a concept of infinity if it's never constructed. Otherwise, one is granting the Platoniist's argument that the sequence already exists.
So in what sense does it mean to say that 1,2,3... goes on ad infinitum?
Welcome to The Philosophy Forum!
Get involved in philosophical discussions about knowledge, truth, language, consciousness, science, politics, religion, logic and mathematics, art, history, and lots more. No ads, no clutter, and very little agreement — just fascinating conversations.
Categories
- Guest category
- Phil. Writing Challenge - June 2025
- The Lounge
- General Philosophy
- Metaphysics & Epistemology
- Philosophy of Mind
- Ethics
- Political Philosophy
- Philosophy of Art
- Logic & Philosophy of Mathematics
- Philosophy of Religion
- Philosophy of Science
- Philosophy of Language
- Interesting Stuff
- Politics and Current Affairs
- Humanities and Social Sciences
- Science and Technology
- Non-English Discussion
- German Discussion
- Spanish Discussion
- Learning Centre
- Resources
- Books and Papers
- Reading groups
- Questions
- Guest Speakers
- David Pearce
- Massimo Pigliucci
- Debates
- Debate Proposals
- Debate Discussion
- Feedback
- Article submissions
- About TPF
- Help
More Discussions
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum










