-
 Devans99
2.7kMy interest in maths stops when maths stops telling me about the nature of reality.
Devans99
2.7kMy interest in maths stops when maths stops telling me about the nature of reality.
Transfinite maths and reality are greatly in opposition. ∞+1=∞ tells us that there exists something, that when it is changed, it does not change. This is not the reality I live in. I doubt that it is even possible to define a viable virtual reality that supports the 'features' of transfinite maths - how can something change and not change at the same time?
I believe that for example, non-euclidean geometry maybe telling us something about our reality and it is possible to build logical virtual realities on that basis. But infinite set theory... no. -
 ssu
9.7k
ssu
9.7k
No.However, we still have to consider fact 2 by which we can determine inequality of cardinality of sets
The set of natural numbers N = {1, 2, 3, 4,...}
The set of even numbers E = {0, 2, 4, 6,...} — TheMadFool
As we are talking of infinite sets, they aren't 'inequal'. They are indeed 'equal'.
You just take the set of N and multiply every number in N by two and presto! You have the set of even numbers.
It's the same if you would take the set of natural numbers and multiply every number with 1 000 000 and then the new set would be like Sn = ( 0, 1 000000, 2 000000, 3 000000, 4 000000,...) Now you would notice that there's a huge gap between the numbers, 999 999 numbers between every one. But this is simply the strange thing that you get with infinite sets. And basically again this is the Hilbert Hotel, which I remarked on the first page of this thread! (even if the picture seems not to be working)
Again no!It's clear that N can be separated into two proper subsets viz. the set of even numbers V = {0, 2, 4, 6,...} and the set of odd numbers, D = {1, 3, 5, 7,...}
Notice how set E has a bijection with set V and set V is a proper subset of set N. If so, then in accordance with fact 2 above, n(E) < n(N) i.e. the set of even numbers is less than the set of natural numbers.
This presents a problem doesn't it? — TheMadFool
An infinite set is a set which is equivalent to a proper subset of itself. You can find the proofs online, similar as what I gave above. -
 quickly
332. A set G has a cardinality greater than a set H if and only if the there's a bijection between set H and a proper subset of G — TheMadFool
quickly
332. A set G has a cardinality greater than a set H if and only if the there's a bijection between set H and a proper subset of G — TheMadFool
This is false. For example, is a proper subset of and the function is a bijection from to , but the cardinality of both sets is . However, it is classically true that iff there is an injection from to but no surjection. -
TheMadFool
13.8kHowever, it is classically true that A<BA<B iff there is an injection from AA to BB but no surjection. — quickly
Again no! — ssu
I think @fishfry said something to the effect that bijection has precedence of injection. Why?
I think @quickly understood my argument but s/he still has to explain @fishfry:
If there exists a bijection between two sets, even a single one, even if there are plenty of functions that aren't bijections, then we DEFINE the two sets as being cardinally equivalent. It's a definition, not a proof. — fishfry -
 ssu
9.7k
ssu
9.7k
I'm not sure what he meant, but a bijection is both an injection and a surjection.I think fishfry said something to the effect that bijection has precedence of injection. Why? — TheMadFool
But to your question: a set is infinite if and only if it is equivalent to one of its proper subsets. And this counters your argument. You are making the mistake of thinking about an infinite set as finite.
The proof of this actually refutes your idea: See for example here, Proof 1
You see with a finite set it isn't so: a finite set can not be in one-to-one correspondence with one of its proper subsets. -
TheMadFool
13.8kI'm not sure what he meant, but a bijection is both an injection and a surjection.
But to your question: a set is infinite if and only if it is equivalent to one of its proper subsets. And this counters your argument. You are making the mistake of thinking about an infinite set as finite.
The proof of this actually refutes your idea: See for example here, Proof 1
You see with a finite set it isn't so: a finite set can not be in one-to-one correspondence with one of its proper subsets. — ssu
Thanks for the reply. I understand that another definition for an infinite set is a set that is equivalent (bijection possible) to a proper subset of itself.
I think I get it now. The proper subset of the infinite set itself has to be infinite. The number of elements in a proper subset B of a finite set A is necessarily less than the number of elements in the set A. n(B) < n(A) so long as A and B are finite.
When we then consider infinite sets X and Y such that X is a proper subset of Y then n(X) = n(Y).
It seems that a difference in terms of members, so long as the proper subset of the other, the parent set, is itself infinite, doesn't translate into a numerical difference.
Imagine A = {s, d, f, h} and the proper subset B = {d, f}
The difference between the two A - B = {s, h} = C can be numerically represented as n(C) = 2
However with infinite proper subsets of infinite sets, the difference is zero.
n(set of natural numbers) - n(set of even numbers) = infinity - infinity = zero because both are, well, infinite. In other words the fact that the set of even numbers don't contain odd numbers and that the set of natural numbers is the union of odd and even numbers didn't translate into a numerical difference like it does with finite sets. -
 sandman
41The set of natural numbers N = {1, 2, 3, 4,...}
sandman
41The set of natural numbers N = {1, 2, 3, 4,...}
The set of even numbers E = {0, 2, 4, 6,...}
Putting all the fancy terms aside, by inspection, in some cases there are even integers in N corresponding to even integers in E. That is a one to one.correspondence only if you ignore the identity of the elements. Eg. there are as many pcs of trash in bag 1 as in bag 2. Then,removing E from both sides, D (odd) = {}.. -
 ssu
9.7k
ssu
9.7k
Yep, you got it! :up:I think I get it now. The proper subset of the infinite set itself has to be infinite.The number of elements in a proper subset B of a finite set A is necessarily less than the number of elements in the set A. n(B) < n(A) so long as A and B are finite. - In other words the fact that the set of even numbers don't contain odd numbers and that the set of natural numbers is the union of odd and even numbers didn't translate into a numerical difference like it does with finite sets. — TheMadFool
This is btw. crucial to understand before the next step: comparing the natural numbers to the reals, which gets people really confused and asking a lot of questions. Just look at the thread Is Cantor wrong about more than one infinity.
Basically in infinite set the real question is can you get the numbers well ordered or not. Every non-empty well-ordered set has a least element. In layman terms, it's a question of can you list the numbers in the infinite set in such fashion that you can be sure to write every number. If you can do that, then the infinite set is of the same size as the natural numbers. -
 quickly
33I think fishfry said something to the effect that bijection has precedence of injection. Why? — TheMadFool
quickly
33I think fishfry said something to the effect that bijection has precedence of injection. Why? — TheMadFool
Hopefully this explains my comment. If is a function from a set to a set , then is
- injective iff implies for all and in ;
- surjective iff for all in there exists an in such that ; and
- bijective iff for all in there exists a unique in such that .
Intuitively, an injection maps unique elements of its domain to unique elements of its range; a surjection has every element of its range mapped to by some element of its domain; and a bijection has every element of its range mapped to by a unique element of its domain. We have the following theorems:
- is bijective iff it is injective and surjective.
- is bijective iff it has an inverse.
You should convince yourself of the following facts. If is
- injective, then there may be some elements of that are not mapped to by any element of ;
- surjective, then there may be some elements of that map to the same element of ; and
- bijective, then there is a unique pairing between elements of and elements of
These observations justify the following definition of an ordering relation on the cardinal numbers:
- iff there is an injection from to ; and
- iff there is a bijection from to
From the above discussion, it should be clear that iff there is an injection from to but no bijection. This means that every injection from to must fail to be surjective (i.e., for every injection there exist elements of that the injection misses, although those elements will be different in different cases).
In classical mathematics, we can show that the ordering relation is total. By "classical," I mean mathematics with the axiom of choice. If we assume a constructive framework where the axiom of choice (law of excluded middle, double negation elimination, etc.) fails, the discussion becomes more complicated. IIRC, the "bijection between a set and a proper subset of itself" definition of infinity fails in a constructive setting, you cannot show that the ordering relation is total, an injective function does not imply the existence of a surjection from its image to its domain, and so forth.
I think Enderton's Elements of Set Theory is a good introduction to these topics. -
TheMadFool
13.8k
Can you have a look at what I said below. It seems wrong and right.
n(set of natural numbers) - n(set of even numbers) = infinity - infinity = zero because both are, well, infinite. — TheMadFool
Consider two infinite sets A and B of equal cardinality i.e. n(A) = n(B) = infinity
Shouldn't n(A) - n(B) = 0?
Yet n(set of natural numbers, infinite) - n(set of even numbers, infinite) = n(set of odd numbers, infinite) which is infinite indicating that infinity - infinity = infinity
Thanks. I'll just stick to the simple.injective, then there may be some elements of BB that are not mapped to by any element of AA;
surjective, then there may be some elements of AA that map to the same element of BB; and
bijective, then there is a unique pairing between elements of AA and elements of B — quickly -
 quickly
33Thanks. I'll just stick to the simple. — TheMadFool
quickly
33Thanks. I'll just stick to the simple. — TheMadFool
You can't do that.
Can you have a look at what I said below. — TheMadFool
The subtraction operation on infinite cardinals is not well defined. For example, let denote the set of even numbers and the set of odd numbers. It is easy to see that
- ;
- ;
- ; and
- .
However,
- ; and
Thus, we cannot say that or . There are some technical conditions under which you can define a subtraction operation, but they are beyond the scope of this question. -
 jgill
4kThe proper subset of the infinite set itself has to be infinite — TheMadFool
jgill
4kThe proper subset of the infinite set itself has to be infinite — TheMadFool
Really? Consider N={1,2,3,...} and S={1,9} No 1:1 correspondence. You are missing "equivalence"
"A" proper subset? Not "The", I think. -
TheMadFool
13.8kReally? Consider N={1,2,3,...} and S={1,9} No 1:1 correspondence. You are missing "equivalence"
"A" proper subset? Not "The", I think. — John Gill
You quoted me out of context. Thanks anyway. -
 ssu
9.7kCan you have a look at what I said below. It seems wrong and right.
ssu
9.7kCan you have a look at what I said below. It seems wrong and right.
n(set of natural numbers) - n(set of even numbers) = infinity - infinity = zero because both are, well, infinite.
— TheMadFool
Consider two infinite sets A and B of equal cardinality i.e. n(A) = n(B) = infinity
Shouldn't n(A) - n(B) = 0?
Yet n(set of natural numbers, infinite) - n(set of even numbers, infinite) = n(set of odd numbers, infinite) which is infinite indicating that infinity - infinity = infinity — TheMadFool
Remember that Infinity is an endless series, not a number. Many would disagree with you if you treated infinity as a number! Some would say that infinity minus infinity is indeterminate. The following are considered to be indeterminate in form:
If you think that taking out the even numbers from the natural numbers you'll the odd numbers left, then you are thinking of a finite set. A finite set can not be in one-to-one correspondence with one of its proper subsets while an infinite one can be. Remember that you are talking about sets that are of INFINITE length. And because they are infinite, then you have the rule that part is as large as the whole: an infinite set is a set which is equivalent to a proper subset of itself. -
 jgill
4k
jgill
4k
Consider two infinite sets A and B of equal cardinality i.e. n(A) = n(B) = infinity
Shouldn't n(A) - n(B) = 0? — TheMadFool
Beyond finite instances, cardinalities are not numbers. They are equivalence classes. -
TheMadFool
13.8kBeyond finite instances, cardinalities are not numbers. They are equivalence classes. — John Gill
Thanks. I get it, more or less. -
 sandman
41If 'the cardinality of N and E are equal', means there are as many elements in
sandman
41If 'the cardinality of N and E are equal', means there are as many elements in
N as E, I can accept that. That however does not justify the statement 'there are as many even integers as integers. The first statement is about a measure of a set, the second is about the identity of the elements, which contradicts statistics. Math concepts should be consistent. -
 sandman
41
sandman
41
Infinity is not an integer, or any type of number, and definitely not a quantifier.They think aleph-naught is, or acts like, just another integer, — tim
It's a relation/condition of having no limit or boundary. Measurement requires boundaries. The application of 'rules of measurement for finite objects' cannot be applied to 'infinite objects. 'To measure an immeasurable object' is a contradiction of terms No one has yet explained how to measure a stick with one end (of infinite length). His extended alephs depend on his diagonal argument which is false, since he doesn't explain why the complementary sequence is already there before he constructs the one that isn't there! His work in other areas of math may be satisfactory, but there is a category for his 'supernatural revelation' of transfinite numbers, 'recreational mathematics'. He was a self appointed spokesman, and always anxious about his status in the mathematical community. It helps to research the person and their motivation before and during their theorizing. If you propose an idea from an authority figure, that would surely promote credibility. Then use symbols from the Hebrew alphabet! It sounds more like a public relations promotional strategy than a mathematical conception.
There is no issue of comprehension concerning 'infinity' as a useful abstraction, as in most of science, vs reality. The issue is knowing the difference.
I still haven't seen the average household with 2.3 children.
A quote by Cantor in his favor:
Ewald, W., From Kant to Hilbert, Oxford 1996.
"The old and oft-repeated proposition “Totum est majus sua parte” may be applied without proof only in the case of entities that are based upon whole and part; then and only then is it an undeniable consequence of the concepts “totum” and “pars”. Unfortunately, however, this “axiom” is used innumerably often without any basis and in neglect of the necessary distinction between “reality” and “quantity”, on the one hand, and “number” and “set”, on the other, precisely in the sense in which it is generally false. [An] example may help to explain. Let M be the totality (n) of all finite numbers n, and M¢ the totality (2n) of all even numbers 2n. Here it is undeniably correct that M is richer in its entity, than M¢; M contains not only the even numbers, of which M¢ consists, but also the odd numbers M¢¢ . On the other hand it is just as unconditionally correct that the same cardinal number belongs to both the sets M and M¢. Both of these are certain, and neither stands in the way of the other if one
heeds the distinction between reality and number."
The issue is the present day interpolation/misinterpretation 'there are as many even integers as integers'. The correspondence is a quantitative comparison of two sets. It is not a comparison of two classes of integers.
M could be the set of traditional married people.
W could be the set of married women.
P could be all male-female pairs formed from M
A 1-1 correspondence from P to W, does not mean 'there are as many women as people'. -
 fishfry
3.4kI accept. I ought to because I've delivered a few and felt justified doing so, so I ought to take if I've earned. — tim wood
fishfry
3.4kI accept. I ought to because I've delivered a few and felt justified doing so, so I ought to take if I've earned. — tim wood
Rock and roll Brother Tim. Thanks for the kind words. It's all good.
I haven't read the intervening posts so perhaps some of these points have been covered. I did want to toss in my two cents about uncountable bijections, and how the subject of bijections relates to the subject of well-ordering. In short, it doesn't at this level. It's not an unreasonable thing to think, as I came to learn. But bijections are defined between sets; and sets have no inherent order. The sets {a,b,c} and {c,b,a} are the exact same set. Any maps between them, including bijections, pertain only to the elements and not to any order properties the sets might have.
Of course there are ordered sets, along with the order preserving bijections between them. Among these are the well-ordered sets, which lead to the beautiful topic of the ordinal numbers. I could talk about the ordinals all day. But not right now, because they're peripheral to the subject of basic bijections. I hope you'll take this on faith now, and the following examples will bring out this point. In this post I'll limit myself to discussing bijections.
Now I'm going to walk through six bijections between uncountable sets.
(1) The question arises: Can there be a bijection between uncountable sets?
Suppose there were such a thing. What's the most obvious example we could think of? How about the identity map on the reals; that is, the function given by .
This function should look familiar to everyone who took analytic geometry in high school. Its graph is a straight line through the origin making an angle of 45 degrees or radians with the positive -axis. This is such a familiar mathematical object that we never stop to think that it's a bijection between two uncountable sets.
We now have at least one example of a bijection between uncountable sets. And in passing we've proven a theorem.
Theorem: Every set is cardinally equivalent to itself.
Proof: The set's identity function provides the required bijection.
In other words, cardinal equivalence is a reflexive relation.
(2) Even though the real numbers aren't well ordered, the identity map preserves the usual order on the reals. (The usual order is the one we learned in grade school). So maybe bijections are related to order properties after all??? But no. Consider the bijection from the reals to itself given by everywhere except that , , and .
This bijection does not preserve order, because but . And you can see that we could easily cook up far more complicated nested cycles and loops and tricks that would make bijections as complicated as we want. So we can see that order properties are a separate consideration from whether or not a function is a bijection.
By the way we have a familiar name for a bijection from a set to itself: a permutation. Permutations of finite sets are more familiar to us, but you can permute infinite sets as well. Every permutation of a set is a bijection from that set to itself; and most of them are completely random, they don't preserve order or any other property.
(3) The function between and given by , with inverse function .
This has already been mentioned earlier in the thread. There are two points of interest.
* This bijection shows that bijections do not necessarily preserve length. And in general, bijections don't necessarily preserve measure, the abstract generalization of length, area, volume, etc. A circle of radius 1 is bijectively equivalent to a circle of radius 2. Bijections don't preserve measure. Good to know.
* Both and its inverse are continuous in the sense of freshman calculus. Very informally, their graphs can be drawn without lifting your pencil from the paper.
In the mathematical discipline of topology, two topological spaces are regarded as equivalent if there is such a bi-continuous bijection between them (meaning the bijection and its inverse are both continuous). The intuitive meaning is that we can stretch or shrink or twist one space into the other without ripping or tearing or poking holes. If you've ever seen one of those illustrations of a donut being turned into a coffee cup, that mathematical trick is done using a continuous bijection.
https://en.wikipedia.org/wiki/File:Mug_and_Torus_morph.gif
(4) The continuous bijection between and given by , with inverse .
The tangent function is usually defined as sine over cosine, but it's more helpful to think of it as the function that inputs an angle, and outputs the slope of the line through the origin making that angle with the positive -axis. If you think of a clock with a single hand that goes from 6 counterclockwise to 12, as the angle goes from to , the slope goes from to . That is, the tangent function is a bijection from the open interval to the entire real line . Its inverse, the arctangent, maps the entire real line to the the open interval .
Since both the tangent and the arctangent are continuous, we see that a bounded open interval is topologically equivalent to the entire real line. Not only do bijections fail to preserve finite lengths; they can't even distinguish between finite and infinite lengths. And topology can't tell the difference either. You can take the tiniest imaginable open interval of the real numbers, and stretch it like taffy till it becomes the entire real line.
(5) "Cantor's surprise." For any positive integer , the -dimensional Euclidean space has the same cardinality as the real numbers.
Cantor originally thought that the real numbers had cardinality ; and the plane had cardinality , and Euclidean 3-space had cardinality , and so forth. [In math, dimensional space just means the set of all -tuples of real numbers, with pointwise addition and scalar multiplication by reals, just as with the usual x-y plane and x-y-z space. Nothing to do with "time as the fourth dimension" or rolled-up dimensions in string theory or any other physical interpreation. That's sometimes a point of confusion.]
He was surprised to realize that in fact all finite-dimensional Euclidean spaces have the same cardinality. Here's the proof. We'll show that the open unit interval and the open unit square have the same cardinality. That is, we'll show a bijection between the real numbers strictly between 0 and 1, and the set of ordered pairs in the x-y plane each of whose coordinates are strictly between 0 and 1.
Suppose is a point in the open unit square with decimal representations and respectively. We map the pair to a single real number by interleaving the digits to get .
It's clear that you can reverse this process. Given any real number you can de-interleave its digits to get a pair of real numbers. We can extend the result from the unit interval to the entire real line via the tangent/arctangent. Of course this bijection is highly discontinuous, it has no nice properties at all.
You can clearly interleave -digits this way, and that's the proof. When Cantor discovered this result he wrote to his friend Dedekind: "I see it but I don't believe it!"
We saw earlier that bijections don't necessarily preserve length or volume. Now we see that bijections don't necessarily preserve dimension. It's good to keep in mind the limitations as well as the utility of bijections.
Quibble: One could note that some real numbers have two distinct decimal representation, such as , possibly messing up the bijection. But there are only countably many such problematic reals, and we can formalize the principle that "countable sets never make a difference in uncountability arguments." The problem can be fixed.
(6) Can we find a bijection between and ? There must be one but it's tricky.
First, why must there be a bijection? We've seen earlier that there's a bijection between and the entire real line. And and are both proper subsets of the real line and proper supersets of . So both of those cardinalities are squeezed between two equal cardinalities. In other words if is the cardinality of the set , then:
, but the first and last cardinalities are equal via the tangent/arctangent. So and must have the same cardinality; after all they only differ by a point.
If you've seen the story of the Hilbert hotel, you know that you can always shift each guest to the next higher room, in effect "losing a guest." And if you were to move each guest to the next lower-numbered room, the hotel would still be full and you'd have an extra guest with no room! This is the basic idea behind adding or getting rid of endpoints in all these kinds of problems.
In this case we pick out a countable subset of , and "Hilbert shift" away that pesky 1 at the right end. Here's the function :
[Something funny about the markup, ignore those brl things, the forum software put them in].
Everything gets mapped to itself; except that 1 goes to 1/2, 1/2 goes to 1/4, 1/4 goes to 1/8, and so on. We've "made the 1 disappear" by Hilbert-shifting it to the "next room" as it were, and we have our bijection.
Here's a picture of what happens. 1 goes to 1/2, 1/2 goes to 1/4, and so forth. Every point has somewhere to go, and nothing replaces the point at 1. It disappears like the guest in the first room of the Hilbert hotel.
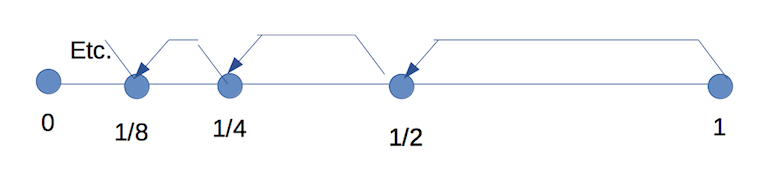
-
 fishfry
3.4kI think fishfry said something to the effect that bijection has precedence of injection. Why? — TheMadFool
fishfry
3.4kI think fishfry said something to the effect that bijection has precedence of injection. Why? — TheMadFool
I have not followed all these posts for a while so I don't know if this is still a point of confusion. I just want to assure you that I never could have possibly said any such thing; for the simple reason that I don't have any idea what that means.
The point that you were hung up on before is that the definition of a bijection says that there exists at least one bijection between two sets. The fact that a million other functions between the sets don't happen to be bijections is irrelevant. It's an existential condition. If it rained for five minutes today and was otherwise sunny, it's still true that "it rained today." I hope someone's been able to clarify that for you. -
 fishfry
3.4kBeyond finite instances, cardinalities are not numbers. They are equivalence classes. — jgill
fishfry
3.4kBeyond finite instances, cardinalities are not numbers. They are equivalence classes. — jgill
Quibble-wise this is not true. Originally, a cardinal was the class of all sets with that cardinality. The trouble is that those classes are proper classes and not sets; and we want to define cardinals as sets so that we can use the rules of set theory on them.
I wrote a longer exposition but I'll just shorthand this and provide the links.
Case 1: Assume the axiom of choice. Then given a set , the axiom of choice says that can be well-ordered; that is, there is some ordinal such that and are in bijection. Since the proper class of ordinals is well-ordered, there must therefore be a least such ordinal that's cardinally equivalent to . We define that as the cardinal of .
For example is the ordinal corresponding to the natural numbers; and by this definition, . And is defined as the first uncountable ordinal, . (Yes there are uncountable ordinals, even without the axiom of choice. How counterintuitive is that!)
Case 2: Assume the negation of choice. Then there's some set that can't be well-ordered so we can't use the idea as in case 1. Instead (I'm going to just fly through this for sake of brevity and supply the links if anyone's interested) the cardinal of a set is the set of sets bijectively equivalent to the given set whose rank is the same as that set. The idea is that each set has a "born on" date called its rank; and the collection of all ranks forms the Von Neumann hierarchy. Each level is a set, and the union of all the levels is the universe of sets. So given some set, we find the level at which it first appears; and we defined its cardinal as the set of all bijectively equivalent sets at that level.
This isn't supposed to make sense if you haven't seen it. As I noted, I drafted but didn't post a much longer exposition of these matters which would not be of interest to anyone who's not already studying advanced set theory.
The main point is that this is how you define cardinal numbers these days. They're no longer equivalence classes of sets that themselves aren't sets. That was a problem so it got fixed at the expense of needing to do some technical work.
https://en.wikipedia.org/wiki/Ordinal_number
https://en.wikipedia.org/wiki/Cumulative_hierarchy
https://en.wikipedia.org/wiki/Von_Neumann_universe
https://en.wikipedia.org/wiki/Scott%27s_trick -
TheMadFool
13.8kThe point that you were hung up on before is that the definition of a bijection says that there exists at least one bijection between two sets. — fishfry
That's what I meant. -
 jgill
4kThe main point is that this is how you define cardinal numbers these days. They're no longer equivalence classes of sets that themselves aren't sets. That was a problem so it got fixed at the expense of needing to do some technical work. — fishfry
jgill
4kThe main point is that this is how you define cardinal numbers these days. They're no longer equivalence classes of sets that themselves aren't sets. That was a problem so it got fixed at the expense of needing to do some technical work. — fishfry
Interesting. Thanks. Nice exposition. I only took one course in set theory almost sixty years ago and it was Halmos' Naive book. When he started discussing towers and chains it seemed medieval and it was hard to stay motivated.
I recall seeing that problem about [0,1] and [0,1) on a PhD exam some years ago. I don't think I would have gotten it in the time allowed! :worry:
Welcome to The Philosophy Forum!
Get involved in philosophical discussions about knowledge, truth, language, consciousness, science, politics, religion, logic and mathematics, art, history, and lots more. No ads, no clutter, and very little agreement — just fascinating conversations.
Categories
- Guest category
- Phil. Writing Challenge - June 2025
- The Lounge
- General Philosophy
- Metaphysics & Epistemology
- Philosophy of Mind
- Ethics
- Political Philosophy
- Philosophy of Art
- Logic & Philosophy of Mathematics
- Philosophy of Religion
- Philosophy of Science
- Philosophy of Language
- Interesting Stuff
- Politics and Current Affairs
- Humanities and Social Sciences
- Science and Technology
- Non-English Discussion
- German Discussion
- Spanish Discussion
- Learning Centre
- Resources
- Books and Papers
- Reading groups
- Questions
- Guest Speakers
- David Pearce
- Massimo Pigliucci
- Debates
- Debate Proposals
- Debate Discussion
- Feedback
- Article submissions
- About TPF
- Help
More Discussions
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum







