-
 Ulrik
21Dear philosophers,
Ulrik
21Dear philosophers,
I'm trying to wrap my head around philosophical logic and in a short introduction I read I came across this basic syllogism, well I made this one up but I think it's logically the same as in the book:
All beautiful houses are valuable.
All castles are valuable.
therefore
All castles are beautiful houses.
Now the book says this conclusion is incorrect, it does not follow from the premises. I fail to see why. If we focus only on the premises, then since both are equivalent to being valuable, they have to be equal to each other. In letters:
For any A it is the case that they are B
For any C it is the case that they are B
Since A = B and C = B, and B = B, it follows that A = C, and the conclusion should be correct. However I know it is mistaken, so my question is, what do I not understand? Where is the error in my reasoning?
The book seems to hint that the meaning of valuable is somehow a greater category that includes both castles and beautiful houses, and this category is so broad it does not necessarily follow that castles and beautiful houses are the same. But this broad meaning is nowhere to be found in the premises alone, so how could I know that and incorporate that in the reasoning?
Thanks for your input! -
TheMadFool
13.8kThe middle term “valuable things” isn’t distributed.
This is the simplest logical fallacy for me to understand.
The argument is:
1. All beautiful houses are valuable things
2. All castles are valuable things
Therefore
3. All castles are beautiful houses
The connection between castles and beautiful houses is valuable things. So it seems reasonable that one of the premises should be a statement about ALL valuable things to make the connection strong as possible.
Fallacy of the undistributed middle term. -
 SophistiCat
2.4kYour mistake is that you interpret "are" as identity (=), whereas from the context it should be clear that "are" here indicates membership of a class (of valuable things).
SophistiCat
2.4kYour mistake is that you interpret "are" as identity (=), whereas from the context it should be clear that "are" here indicates membership of a class (of valuable things).
Such things are easier to understand if you draw a Venn diagram:
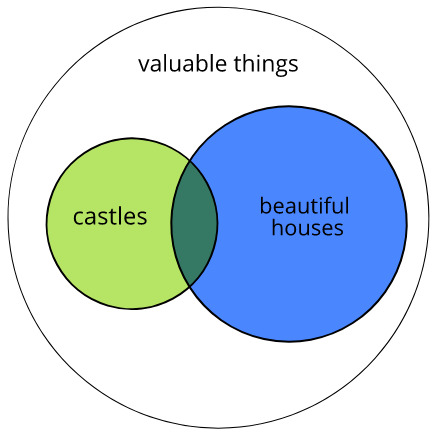
-
 Ulrik
21
Ulrik
21
Hello MadFool,
Thanks for your reply. I am not familiar with the technical jargon of distribution. But yes, I can see that being valuable is the common ground. Not sure how that makes the reasoning in my 1st post invalid. -
 Ulrik
21
Ulrik
21
Hello SophistiCat,
Thanks for your reply.
Yes, you are right, I interpreted 'are' as 'being equal to', not as class membership. Is thinking in class memberships the right way to approach syllogisms in general? I find it hard to determine what context I can, and cannot use, since, as I understand it now, in logic, we ignore anything that's not in the premises.
But how about this famous argument from Aristotle, where he says:
If A is equal to B, and B is equal to C, then A is equal to C.
In this case we have to interpret 'equal to' as identical to, not as class membership?
If A = B and C = B, then A = C would be correct in that case. -
 Ulrik
21Remaining on the topic I found another tricky syllogism, which I approached by drawing a Venn-diagram, like you did.
Ulrik
21Remaining on the topic I found another tricky syllogism, which I approached by drawing a Venn-diagram, like you did.
This is the argument:
No decent people curse
Americans curse
Therefore
Some Americans are not decent
The book says this conclusion is valid. I fail to see why. I answered invalid, because based on the premises it says 'all Americans are not-decent', not just 'Some Americans are not decent'.
Here's the Venn-diagram I drew, would be cool to know if I drew it correctly or not, I feel like if I can become good at drawing these diagrams I can finally understand logic.
[img]http://
-
 SophistiCat
2.4kYes, you are right, I interpreted 'are' as 'being equal to', not as class membership. Is thinking in class memberships the right way to approach syllogisms in general? I find it hard to determine what context I can, and cannot use, since, as I understand it now, in logic, we ignore anything that's not in the premises. — Ulrik
SophistiCat
2.4kYes, you are right, I interpreted 'are' as 'being equal to', not as class membership. Is thinking in class memberships the right way to approach syllogisms in general? I find it hard to determine what context I can, and cannot use, since, as I understand it now, in logic, we ignore anything that's not in the premises. — Ulrik
You would have to use a formal language to avoid ambiguities (e.g. ⊂ vs. =), but for relatively simple reasoning this isn't necessary. You just need to apply common sense or knowledge of the context to come up with the right interpretation.
But how about this famous argument from Aristotle, where he says:
If A is equal to B, and B is equal to C, then A is equal to C.
In this case we have to interpret 'equal to' as identical to, not as class membership?
If A = B and C = B, then A = C would be correct in that case. — Ulrik
IIRC this is true in Aristotelian logic, where certain types of predicates are simply assumed to be transitive. So this result wouldn't require proof. -
 Ulrik
21
Ulrik
21
Cheers. When interpretation comes into play, I've learned I'm usually interpreting it wrongly. Common sense I find not obvious at all.
Would be cool if you could take a peak at the Venn-diagram I drew and the error in my reasoning there too. See the post above yours. -
 SophistiCat
2.4kNo decent people curse
SophistiCat
2.4kNo decent people curse
Americans curse
Therefore
Some Americans are not decent — Ulrik
First, it is not entirely clear whether "Americans curse" means "Some Americans curse" or "All Americans curse." (Applying real-world knowledge, it seems more likely that they meant "Some Americans curse" - surely, there are Americans who don't curse?)
Fortunately, the conclusion "Some Americans are not decent" follows either way.
based on the premises it says 'all Americans are not-decent', not just 'Some Americans are not decent'. — Ulrik
But "all Americans are not-decent" implies "Some Americans are not decent," so the conclusion is still true. A valid argument does not have to have the most comprehensive conclusion possible. -
 unenlightened
10kwould be cool to know if I drew it correctly or not, I feel like if I can become good at drawing these diagrams I can finally understand logic. — Ulrik
unenlightened
10kwould be cool to know if I drew it correctly or not, I feel like if I can become good at drawing these diagrams I can finally understand logic. — Ulrik
Start off drawing three intersecting circles, giving 8 regions - outside all, A, B, C, A&B, B&C, C&A, and A&B&C in the middle. Then an 'all' or 'none' premise will declare some region(s) to be empty, whereas a 'some' premise will declare some region(s) to be populated. Shade out the empty regions, and put an X in the populated ones, (or on the border if there are two possible regions).
Then, if the conclusion is valid, it will not tell you to do anything you haven't already done, or to undo anything you have done.
If you try this on your example above, you will see how the validity depends on the interpretation of the premise 'Americans curse'. If you interpret it (as you have in your diagram) as 'All Americans curse', then the conclusion should be 'No Americans are decent', whereas if you interpret it as 'Some Americans curse', then 'Some Americans are not decent' should be the conclusion.
See the wiki entry especially the section on existential import. -
 Ulrik
21
Ulrik
21
Hello SophistiCat, thanks again for your reply. What I gather from it is that, indeed, there is some vagueness in the premises. What I fail to understand however is that you can conclude 'Some Americans curse' from the premise 'All Americans curse'. You see, I thought if one says 'Some people are nice', one means that 'some people are nice, and some are not', rendering the deduction from 'All people are nice' impossible. Basically, why is this valid:
All A's are B's
Therefore
Some A's are B's
While I take the 2nd premise to mean: Some A's are B's and some are not. Since some A's are not B's, the conclusion cannot follow from the premise.
Sorry if this makes it all too complicated. But it's a basic confusion that will return often in logic I have the intuition. -
 Ulrik
21
Ulrik
21 -
 fdrake
7.2k
fdrake
7.2k
In your first diagram, if all Americans curse, the entire circle of Americans should be inside of the entire circle of cursing people. This is like the logic that 'all hawks are raptors' or 'all pens are writing implements' or 'all humans are mortal'.
If it helps, there's a way of thinking of Venn diagrams in terms of sets - collections of objects. If we have 'all humans are mortal', say, this says that the collection of humans; that's you, me, everyone else; is a sub-collection of mortals; that's you, me, everyone else, everything else that dies.
This 'everything else that dies' means that the circle of 'humans' resides strictly within the circle of 'mortals'.
How this relates to implication and arguments is that when one circle (a smaller one) resides entirely within another (a bigger one), we can say that if something is in the smaller one then it is also in the bigger one. This is entirely equivalent to saying that if something is human then it is mortal.
Applying this to your Americans curse example. The Venn diagram for the assumption that 'All Americans curse' are:
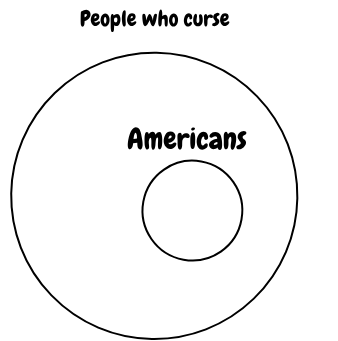
whereas for the assumption that 'some Americans curse' it is:
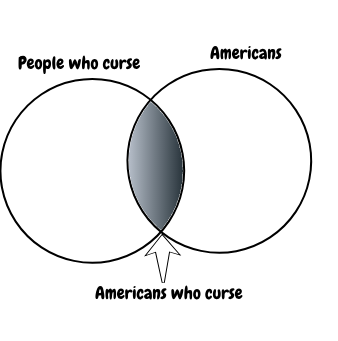
The translation from 'All Americans Curse' to an 'if-then' statement would be 'If something is an American then it curses', and it works in the way I just described. The next bit has some extra detail, if you feel you understand the points I've made so far, you might get something out of it, otherwise keep trying simple examples.
-------
In the case where 'All Americans curse' it's also true to say 'Some Americans curse'. But 'All Americans curse' is a stronger statement than 'some Americans curse'. In terms of the Venn diagrams, 'some Americans curse' means that the circles for 'people who curse' and 'Americans' overlap a bit, whereas 'All Americans curse' means that the circle for 'Americans' resides entirely within the circle for 'people who curse'. The important difference here is that when there's only a bit of overlap - when we can't say that all Americans curse, but we can say that some Americans curse - this means that there is at least one American who does not curse. There being 'at least one American who does not curse' is equivalent to the circle of 'Americans' not entirely residing within the circle of people who curse - if you've been following along, 'the circle of Americans not entirely residing within the circle of people who curse' is completely consistent with 'the circle of Americans and the circle of people who curse have NO overlap at all', which means 'no Americans curse'; or 'there are no Americans who curse', or 'if someone curses, they are not an American'.
' -
 unenlightened
10kIn your first diagram, if all Americans curse, the entire circle of Americans should be inside of the entire circle of cursing people. — fdrake
unenlightened
10kIn your first diagram, if all Americans curse, the entire circle of Americans should be inside of the entire circle of cursing people. — fdrake
Well damn you for a methodological heretic! :naughty:
I just told him the opposite; to put in the entirety of possiblilities first, and then eliminate regions and populate regions according to the premises. This method has the advantage that the same diagram structure can illustrate the relations between the various syllogistic forms as per wiki link above. I also think it is easier to spot errors.
In the case where 'All Americans curse' it's also true to say 'Some Americans curse'. But 'All Americans curse' is a stronger statement than 'some Americans curse'. In terms of the Venn diagrams, 'some Americans curse' means that the circles for 'people who curse' and 'Americans' overlap a bit, whereas 'All Americans curse' means that the circle for 'Americans' resides entirely within the circle for 'people who curse'. The important difference here is that when there's only a bit of overlap - when we can't say that all Americans curse, but we can say that some Americans curse - this means that there is at least one American who does not curse. — fdrake
But here you are just wrong. The usual convention is that universals have no existential import, such that "All Martians curse" does not imply that there are any Martians, but merely denies that there are any that do not curse. Whereas "Some Americans curse" implies that there is at least one American that curses, and specifically and definitely does not mean that there is, or is not, an American that does not curse. In this sense syllogistic meaning departs somewhat from ordinary usage -
 SophistiCat
2.4kWhat I fail to understand however is that you can conclude 'Some Americans curse' from the premise 'All Americans curse'. You see, I thought if one says 'Some people are nice', one means that 'some people are nice, and some are not', rendering the deduction from 'All people are nice' impossible. — Ulrik
SophistiCat
2.4kWhat I fail to understand however is that you can conclude 'Some Americans curse' from the premise 'All Americans curse'. You see, I thought if one says 'Some people are nice', one means that 'some people are nice, and some are not', rendering the deduction from 'All people are nice' impossible. — Ulrik
You are not wrong. Indeed, in natural speech, when we say "some A's are B," more often than not we mean that some are and some aren't. If we want to convey the other meaning, we might say something like "at least some A's are B." However, in the context of logic, in semi-formal syllogisms like the above, "some" is conventionally taken to express the latter meaning, that is
In set terminology: A ∩ B ≠ Ø (the intersection between all A's and all B's is not empty)
In predicate terminology: ∃x: Ax ∨ Bx (there exist subjects to which both predicates apply) -
 fdrake
7.2kI just told him the opposite; to put in the entirety of possiblilities first, and then eliminate regions and populate regions according to the premises. This method has the advantage that the same diagram structure can illustrate the relations between the various syllogistic forms as per wiki link above. I also think it is easier to spot errors. — unenlightened
fdrake
7.2kI just told him the opposite; to put in the entirety of possiblilities first, and then eliminate regions and populate regions according to the premises. This method has the advantage that the same diagram structure can illustrate the relations between the various syllogistic forms as per wiki link above. I also think it is easier to spot errors. — unenlightened
This is a better way of reasoning with Venn diagrams. However, I think it requires familiarity with how to set them up, which hasn't been demonstrated here.
But here you are just wrong. The usual convention is that universals have no existential import, such that "All Martians curse" does not imply that there are any Martians, but merely denies that there are any that do not curse. Whereas "Some Americans curse" implies that there is at least one American that curses, and specifically and definitely does not mean that there is, or is not, an American that does not curse. In this sense syllogistic meaning departs somewhat from ordinary usage — unenlightened
Absolutely right. I figured that vacuous truths would muddy the waters, considering that having a good understanding of why vacuous truths work requires understanding the duality of existential and universal quantifiers (for all = not for some not, for some = not for all not). This understanding isn't in place here, and I believe the purpose of instruction here is to make Venn diagrams and their connection with formal reasoning intuitive, rather than to provide a fully accurate and nuanced account. -
 Ulrik
21Hello fdrake & unenlightened,
Ulrik
21Hello fdrake & unenlightened,
Thank you for your input. I think I understand, or at least I understand it better now, despite some conflicting instructions :wink:
@Sophisticat
Thank you for your reply. Still not sure how one can make a deduction like this:
All people wear blue jackets
therefore
Some people wear blue jackets
However if we start with the conclusion here, and take it as a premise or a statement, then I do see that it means or could mean that 'there is at least one person that is wearing a blue jacket'. Though to be perfectly honest, in natural speech, when I use 'some', I think of more than one person, say a group of 10 people, and when I say 'some are wearing blue jackets', I would mean like 2 or 3, not just one. If it was just the one, I would have said: 'There is one person wearing a blue jacket'.
Long story short, should I just take it as a rule or convention when I encounter in Logic the statement 'All A's are B's', you can validly deduce 'Some A's are B's', despite natural speech?
Welcome to The Philosophy Forum!
Get involved in philosophical discussions about knowledge, truth, language, consciousness, science, politics, religion, logic and mathematics, art, history, and lots more. No ads, no clutter, and very little agreement — just fascinating conversations.
Categories
- Guest category
- Phil. Writing Challenge - June 2025
- The Lounge
- General Philosophy
- Metaphysics & Epistemology
- Philosophy of Mind
- Ethics
- Political Philosophy
- Philosophy of Art
- Logic & Philosophy of Mathematics
- Philosophy of Religion
- Philosophy of Science
- Philosophy of Language
- Interesting Stuff
- Politics and Current Affairs
- Humanities and Social Sciences
- Science and Technology
- Non-English Discussion
- German Discussion
- Spanish Discussion
- Learning Centre
- Resources
- Books and Papers
- Reading groups
- Questions
- Guest Speakers
- David Pearce
- Massimo Pigliucci
- Debates
- Debate Proposals
- Debate Discussion
- Feedback
- Article submissions
- About TPF
- Help
More Discussions
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum







