-
TheMadFool
13.8kWhen we measure length we specify a unit (cm, inch) and then use this unit to measure lengths of objects. Then we say an object is x cm or inches. Not much of a problem in this but what is essential in ''all'' measurements is regularity. What I mean is that once we define a cm or an inch, the specific length that is a cm or an inch must NOT change. Otherwise measurement would be meaningless.
Regularity - the unit of measurement should be constant.
Now let's see how we measure time. Time is measured in seconds, its multiples or subdivisions. The second, today, is defined in terms of how long it takes for a specific atom to vibrate some number of times.
This seems problematic (for me) because how do we know the vibrations of the atom used to define a second is regular? To me the only way we can decide this is by using another process or phenomenon we know to be regular but then how do we know that particular process or phenomenon is regular? And so on...
A classic case of the chicken-egg problem.
Your thoughts...thanks. -
 t0m
319This seems problematic (for me) because how do we know the vibrations of the atom used to define a second is regular? To me the only way we can decide this is by using another process or phenomenon we know to be regular but then how do we know that particular process or phenomenon is regular? And so on... — TheMadFool
t0m
319This seems problematic (for me) because how do we know the vibrations of the atom used to define a second is regular? To me the only way we can decide this is by using another process or phenomenon we know to be regular but then how do we know that particular process or phenomenon is regular? And so on... — TheMadFool
That's a great point. It looks like we have to trust in some kind of uniformity. But there's also Hume's problem of induction. So the trust in uniformity is also there in the laws themselves that involve time. Science looks to be founded on some basic sense of the order in the world, a sense that it also encourages. -
 noAxioms
1.7k
noAxioms
1.7k
Because you get the exact same result from countless repeatings of the experiment.This seems problematic (for me) because how do we know the vibrations of the atom used to define a second is regular? — TheMadFool
I get different results from the time measurement of my grass to grow 5cm, so using grass growth as a clock works, but not very accurately. Good clocks use very consistent processes. -
 Streetlight
9.1kEr, all you need are two measures you think are regular in relation to each other. If one, or both are not in fact regular, at some point they will go out of sync. If they don't, you're good. And even if they are out of sync, if the divergence isn't too bad, all you have to do is recalibrate every once in a while - like we do with leap years.
Streetlight
9.1kEr, all you need are two measures you think are regular in relation to each other. If one, or both are not in fact regular, at some point they will go out of sync. If they don't, you're good. And even if they are out of sync, if the divergence isn't too bad, all you have to do is recalibrate every once in a while - like we do with leap years. -
 sime
1.2kYes, and the definition of the standard metre is no longer the length of a particular platinum bar contained in a Paris vault, but the distance light travels in a vacuum in a precise time interval ideally measured by etc etc
sime
1.2kYes, and the definition of the standard metre is no longer the length of a particular platinum bar contained in a Paris vault, but the distance light travels in a vacuum in a precise time interval ideally measured by etc etc
In short our metric units are essentially imprecise and are in practice unrelated to a particular standard.
The deeper problem relates to Wittgenstein's observations concerning our notion of sameness. For our notion of when two things are "identical" *isn't* in the sense of them being equivalent in a precisely empirical sense, but in the practical sense that they can be substituted for one another in a language game. -
 Metaphysician Undercover
14.7kNow let's see how we measure time. Time is measured in seconds, its multiples or subdivisions. The second, today, is defined in terms of how long it takes for a specific atom to vibrate some number of times. — TheMadFool
Metaphysician Undercover
14.7kNow let's see how we measure time. Time is measured in seconds, its multiples or subdivisions. The second, today, is defined in terms of how long it takes for a specific atom to vibrate some number of times. — TheMadFool
The second is derived from the minute which comes from the hour, and the day. The day refers to the planetary motion. So one rotation of the planetary motion (which is relatively constant) can be divided into seconds. The number of times a specific atom vibrates in one second can be counted, and observed to be consistent as well. So this is deemed as a constant as well. However, the so-called "constants" are not absolutely constant, so this produces the need to make slight adjustments now and then.
This seems problematic (for me) because how do we know the vibrations of the atom used to define a second is regular? To me the only way we can decide this is by using another process or phenomenon we know to be regular but then how do we know that particular process or phenomenon is regular? And so on... — TheMadFool
So we always compare different activities which appear to be temporal constants, the earth's revolution around the sun, the phases of the moon, the rotation of the earth, vibrations of atoms, the movement of light, etc.. From the comparisons of numerous constants, we can determine which are the more reliable constants than others. If one constant proves to have a slight variance in relation to numerous others, we can make adjustments accordingly, model that variance and look for the cause of that variance. By modeling the variance in planetary motions, the heliocentric theory of the solar system was developed and proven. The orbits of the planets were determined by Kepler to be elliptical rather than circular as postulated by Copernicus maintaining consistency with earlier proposals of the heliocentric system, and Aristotle's metaphysics. This was determined and proven through analysis and reference to the variances. These variances were the stumbling block needed to be overcome to prove the heliocentric system. -
TheMadFool
13.8kBecause you get the exact same result from countless repeatings of the experiment. — noAxioms
How do you know you get the exact same result? By applying a specific standard to both to confirm repeatability of measurement. The next question, of course, is how do you know the standard you chose is regular? Chicken and egg?
Er, all you need are two measures you think are regular in relation to each other. — StreetlightX
Well, that doesn't solve the problem does it? The phenomenon itself must be regular. Taking two faulty rulers to countercheck each other doesn't solve the problem of whether we have the right measurement.
I see your point. Makes sense.
(Y)
However, the so-called "constants" are not absolutely constant, so this produces the need to make slight adjustments now and then. — Metaphysician Undercover
How do we know that? By using, a supposedly accurate, time piece. And how do we know that that's accurate? -
 Streetlight
9.1kWell, that doesn't solve the problem does it? The phenomenon itself must be regular. — TheMadFool
Streetlight
9.1kWell, that doesn't solve the problem does it? The phenomenon itself must be regular. — TheMadFool
What 'phenomenon'? All you want is regularity. If two measures are in sync, they're regular. You really need to stop with the pseudo-problem threads. -
 Metaphysician Undercover
14.7kHow do we know that? By using, a supposedly accurate, time piece. And how do we know that that's accurate? — TheMadFool
Metaphysician Undercover
14.7kHow do we know that? By using, a supposedly accurate, time piece. And how do we know that that's accurate? — TheMadFool
An accurate time piece just utilizes one of the supposed constants. We know that the supposed constants are not absolute, by comparing one to the other, and determining the variances. If we compare numerous constants we can determine which variances are proper to which constants. -
TheMadFool
13.8kWhat 'phenomenon'? All you want after is regularity. If two measures are in sync, they're regular. — StreetlightX
Can you flesh this idea of ''two measures are in sync''. Can you give me a concrete instance of this ''solution''?
I'll give it a try...
Take two pendulums swinging. By ''in sync'' you mean they move to-and-fro at regular intervals. But that's exactly the issue here. How do you know they move, as you say, ''in sync''? -
 Streetlight
9.1kBy ''in sync'' you mean they move to-and-fro at regular intervals. — TheMadFool
Streetlight
9.1kBy ''in sync'' you mean they move to-and-fro at regular intervals. — TheMadFool
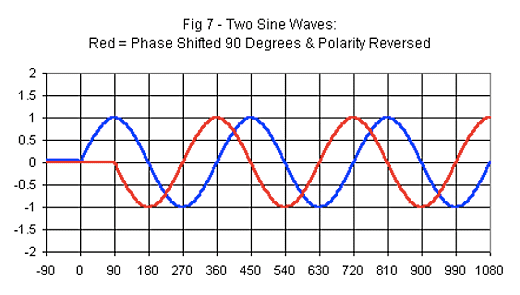
If the frequency of the pendulums is regular and one is, for example, phase shifted by 90 degrees, they should stay 90 degrees phase shifted (the distance between the waves should not change). If the distance remains the same, the frequency of the pendulums is regular, if it doesn't, the frequency of at least one of the waves isn't regular.
It's like asking how one can know if two lines are parallel. If you're in euclidean space, place them side by side perpendicular to a horizon, and no matter how far you draw your horizon, the lines should never meet. Then you know your lines are straight. No need to compare an infinate array of lines. -
 t0m
319Taking two faulty rulers to countercheck each other doesn't solve the problem of whether we have the right measurement. — TheMadFool
t0m
319Taking two faulty rulers to countercheck each other doesn't solve the problem of whether we have the right measurement. — TheMadFool
Right. I think you've opened a nice philosophical can of worms, kind of like Hume's problem of induction. It may not be a practical question, but I do not think it's only a matter of playing with words. I disagree that it's a pseudo-question.
Since 1967, the International System of Units (SI) has defined the second as the duration of 9192631770 cycles of radiation corresponding to the transition between two energy levels of the caesium-133 atom. In 1997, the International Committee for Weights and Measures (CIPM) added that the preceding definition refers to a caesium atom at rest at a temperature of 0 K.[15] — wiki
How would we know 'officially' if the transitions were slowing down or speeding up? They are themselves the 'official' measure. Practically we would see things out sync (other periodic processes would be out of sync with the cesium.) We'd be thrown into a scientific crisis/opportunity. -
 apokrisis
7.8kHow would we know 'officially' if the transitions were slowing down or speeding up? — t0m
apokrisis
7.8kHow would we know 'officially' if the transitions were slowing down or speeding up? — t0m
We know radioactive decay makes a good clock as we also know the physics that could change its rate.
So we have relativity theory which says everything is fine as long as we share the clock's inertial reference frame. If the clock were to get accelerated, then it would read off time differently.
And we have quantum theory to tell us that radioactive decay is an intrinsically independent process. It has a statistics which is "internal" - ruled by a constant of nature. Although again, we could affect that by "observing the decay continuously", preventing its spontaneous probabilistic decay - something called the quantum zeno effect.
So in principle, the "clock of the universe" could speed up or slow down and we couldn't notice it. But it is the fact itself that we couldn't notice a difference that then means there ain't anything to worry about - except people's metaphysical hankering for externalist accounts of reality.
We have rules - relativity and quantum theory - to handle the way time can be stretched or broken in ways we can notice. We can understand how clocks can tell a different time because of physical differences. And so, to the degree we remove those difference-making conditions, our clocks will "run true".
This may only be an internalist truth. But in the end, only internalism makes sense as epistemology. -
 t0m
319And we have quantum theory to tell us that radioactive decay is an intrinsically independent process. — apokrisis
t0m
319And we have quantum theory to tell us that radioactive decay is an intrinsically independent process. — apokrisis
What do you make of Hume's problem of induction? I have no real doubt about the uniformity of nature, but it seems to me that quantum theory is founded in our trust in this uniformity. In theory, all the order we have come to trust in could go to hell. Admittedly this would probably wipe out our ability to notice this going-to-hell. We'd die instantly. But isn't it logically possible ? I don't expect to be suddenly wiped out by a change in the 'laws' of nature, but I have yet to see a way around Hume's
'problem.'
So in principle, the "clock of the universe" could speed up or slow down and we couldn't notice it. But it is the fact itself that we couldn't notice a difference that then means there ain't anything to worry about - except people's metaphysical hankering for externalist accounts of reality. — apokrisis
I think you're assuming a 'nice' version of the scenario. If things that 'should' be in sync go out of sync, then we'd be thrown into the crisis of deciding which 'law' had been violated. We would of course to include this violation in a still more general law. We can of course postulate the law of the change of the laws. But I don't see how we aren't always relying on an intuitive faith in the uniformity of nature.
Note that I can only 'doubt' this faith theoretically, so there's no question of disregarding science here. It is almost sanity itself to project uniformity on nature. -
 apokrisis
7.8kI don't expect to be suddenly wiped out by a change in the 'laws' of nature, but I have yet to see a way around Hume's 'problem.' — t0m
apokrisis
7.8kI don't expect to be suddenly wiped out by a change in the 'laws' of nature, but I have yet to see a way around Hume's 'problem.' — t0m
Where there is belief, doubt is also possible by definition. Saying A always logically permits not-A if A is in fact a meaningful thing to assert.
So the problem of induction isn't really a problem. If we couldn't doubt, how could we say we believed?
And then uniformity is just a reasonable assumption - the rational bottom-line. How can we measure a difference except against a baseline of indifference? We can't even properly, logically, conceive of a universe in which time ran faster or slower unless we first conceive of it running with some rate that would be, by contrast, constant - the rate without any difference. -
 t0m
319So the problem of induction isn't really a problem. If we couldn't doubt, how could we say we believed? — apokrisis
t0m
319So the problem of induction isn't really a problem. If we couldn't doubt, how could we say we believed? — apokrisis
I take your point, but Hume could squeeze out enough theoretical doubt to make the issue conspicuous. I think the OP does the same thing. Maybe it's not something we can take 'seriously' away from the intellectual pleasure involved in this making conspicuous. But that's true of lots of metaphysics. A thoroughly practical mind might grudgingly/generously call it poetry or conceptual art as opposed to nonsense.
I'm not accusing you of this, but it's easy to imagine a 'smug quietism' misreading genuine logical tensions as language on holiday, complacently waiting for the acknowledgement of such tensions to become conventional, respectable. Why is the 'meaning of being' not a pseudo-question while the OP is? Is this completely divorced from the public dominance of this or that thinker? Are any of us immune to the pressure to be intellectually respectable? -
 apokrisis
7.8kit's easy to imagine a 'smug quietism' misreading genuine logical tensions as language on holiday, complacently waiting for the acknowledgement of such tensions to become conventional, respectable. — t0m
apokrisis
7.8kit's easy to imagine a 'smug quietism' misreading genuine logical tensions as language on holiday, complacently waiting for the acknowledgement of such tensions to become conventional, respectable. — t0m
But this particular issue has had really heavyweight analysis within the metaphysics of physics.
https://en.wikipedia.org/wiki/Hole_argument
https://en.wikipedia.org/wiki/G%C3%B6del_metric
https://en.wikipedia.org/wiki/Bucket_argument
Einstein, Godel and Mach are some pretty impressive thinkers. If physics doesn't seem to worry too much about "the speed of time", it is because analysis says "everything is relative". -
 t0m
319
t0m
319
Is this relativity itself relative? Or understood as an absolute? And was it not established on an assumption of the uniformity of nature? How could any theory be confirmed or survive attempts to falsify it apart from the assumption of the uniformity of nature? If you know of a potent retort to Hume's problem, I'll check it out. -
 fishfry
3.4kAll measurement is approximate anyway, and any drift in the vibrational frequency of cesium atoms is probably orders of magnitude smaller than the measurement error.
fishfry
3.4kAll measurement is approximate anyway, and any drift in the vibrational frequency of cesium atoms is probably orders of magnitude smaller than the measurement error.
Measurement works as long as it's useful. The technology of measurement moves forward together with the progress of all other technology and science. In the end there really is no such thing as a second. There's no law that there are 60 of the in a minute, that comes from the Babylonians who liked base 60. The units of time are whatever humans say they are. They're not part of nature. You can say that time is part of nature. And the cesium atom, that's a part of nature. But the definition of a second, that's not a part of nature. That's something humans did.
By the way I looked up the actual definition.
The second is the duration of 9 192 631 770 periods of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the cesium 133 atom.
https://physics.nist.gov/cuu/Units/second.html -
 apokrisis
7.8kIs this relativity itself relative? Or understood as an absolute? — t0m
apokrisis
7.8kIs this relativity itself relative? Or understood as an absolute? — t0m
Of course it is itself relative. It's a scientific theory and so accepts an internalist inductive argument - the triadic arc of abductive hypothesis, deductive theory, and inductive confirmatory test.
If it claimed anything absolute, that would be externalism.
And was it not established on an assumption of the uniformity of nature? — t0m
Again, what else could count as a reasonable hypothesis? To explain differences that make a difference, you have to presume some baseline where any differences don't. That is what makes measurement even a possibility.
And if science didn't work, we would have given it up long ago (and never in fact arrived at where we are now.) -
 t0m
319
t0m
319
To be clear, science is great. We have no choice. Doubts of the uniformity of nature are theoretical. They are 'silly.' But they are fascinating. To me the problem of induction is beautiful like a chess problem. How strange it is. What initially delighted me about it was that it was sologically revealed. Thinking opens a strangeness that was invisible. If this isn't practical, who said thinking should always be practical? For me the practical is valuable to some degree because it opens up the free time to enjoy reality aesthetically. -
 fishfry
3.4kSo the Planck constant is a social construction and not a part of nature? -https://en.wikipedia.org/wiki/Planck_time — apokrisis
fishfry
3.4kSo the Planck constant is a social construction and not a part of nature? -https://en.wikipedia.org/wiki/Planck_time — apokrisis
As I understand it, the Planck constant is defined in terms of meters^2 times kilograms per second. The physical phenomenon is part of nature, but the units are the work of man. If we defined a kilogram differently we'd get a different number for the Planck constant. It would still be the same value in nature, but it would be described by a different real number in a different system of units.
The underlying physical phenomenon that causes there to be a Planck constant is a part of nature. How we define it is the work of man. In that sense, what we call a second is the work of man. If we had picked say, one and a half of our seconds and called that a second, all the constants in physics would change but no fundamental laws would change at all. We'd just rescale everything. -
 apokrisis
7.8kDoubts of the uniformity of nature are theoretical. They are 'silly.' But they are fascinating. — t0m
apokrisis
7.8kDoubts of the uniformity of nature are theoretical. They are 'silly.' But they are fascinating. — t0m
How so? It is a metaphysically logical position.
Nothing can be definitely talked about except in terms of being measurably "other". If you want to talk about non-uniformity - as in a rate of time that could vary - then there is no choice but to talk about that in contrast to a rate that is uniform.
It isn't some unjustified whim. It is the way metaphysical-strength logic works. -
 apokrisis
7.8kAs I understand it, the Planck constant is defined in terms of meters^2 per kilogram per second. — fishfry
apokrisis
7.8kAs I understand it, the Planck constant is defined in terms of meters^2 per kilogram per second. — fishfry
If you check it out, you will see that "the Planck time comes from dimensional analysis".
So you may as well set every value to 1. The dimensioned units fall out of it. We are talking only of the reciprocal relations that connect the three corners of a triad - c, G and h. We are talking about a relation with irreducible internal complexity.
So we peered into the heart of nature and found - this bare triadic relation. We have G to scale any departure from continuous flatness, h to scale any departure from discrete curvature, and c to scale the "rate" at which the G and h can "communicate".
So what we call "time" is an aspect of a triadic knot, a fundamental hierarchical relation.
In simplistic terms, the Planck time is the view of the knot that gets emphasised when you draw out its knotted relation in this fashion - hG/c. (The fuller equation is (hG/c^5)1/2.)
So the dimensioned units do drop out of the story. You can set all the units involved to 1. And then you are left with this triadic knot that ties together three things in irreducible/reciprocal, fashion - h, G and c.
So time doesn't "exist" itself in some fundamental Newtonian way. It is emergent from this triadic relation. The equation for the Planck time is the formula for making that particular kink in the knot "flat enough" to act as a measurement baseline. -
TheMadFool
13.8kI see. So we can simply take two objects that are ''in sync'' and take that as a measure of regularity? How do we check for synchronization? I think it'll be imprecise. -
 apokrisis
7.8kSo we can simply take two objects that are ''in sync'' and take that as a measure of regularity? How do we check for synchronization? I think it'll be imprecise. — TheMadFool
apokrisis
7.8kSo we can simply take two objects that are ''in sync'' and take that as a measure of regularity? How do we check for synchronization? I think it'll be imprecise. — TheMadFool
SX is wrong if he suggests the clocks could be used to check each other in this fashion in any absolute sense. But in a relative fashion, that's fine.
You can definitely tell if two clocks start to beat a different time. And from there, you can make an inductive case for why that might be. One clock might be faulty. Or in fact someone might be secretly accelerating it. And one of those explanations might have the grounds to be the more likely.
The same is the case if the two clocks keep perfect synchrony. It could be that one is being accelerated, and yet also it is faulty to exactly the degree needed to compensate. We are now talking of something that both remains a possibility yet is completely unlikely. And so two clocks are better than one as a constraint on such uncertainties. -
 Streetlight
9.1kYou can use your eyes, for one. Or more precise apparatuses if avaliable or necessary. But this is a question of experimental design, not principle. And the principle is what matters.
Streetlight
9.1kYou can use your eyes, for one. Or more precise apparatuses if avaliable or necessary. But this is a question of experimental design, not principle. And the principle is what matters. -
 Metaphysician Undercover
14.7kThe same is the case if the two clocks keep perfect synchrony. It could be that one is being accelerated, and yet also it is faulty to exactly the degree needed to compensate. — apokrisis
Metaphysician Undercover
14.7kThe same is the case if the two clocks keep perfect synchrony. It could be that one is being accelerated, and yet also it is faulty to exactly the degree needed to compensate. — apokrisis
That's why we need numerous different types of clocks. Each has its own peculiarities. -
 apokrisis
7.8kThat's why we need numerous different types of clocks. Each has its own peculiarities. — Metaphysician Undercover
apokrisis
7.8kThat's why we need numerous different types of clocks. Each has its own peculiarities. — Metaphysician Undercover
Nope. We need the single best process that could be used at any time and any place. Radioactive decay would be that. Or some similar "free" quantum process. -
TheMadFool
13.8kAnd the principle is what matters. — StreetlightX
Well, regularity is absolutely necessary and you agree on that.
I'm still not convinced about this so please be patient.
I'll stick to pendulums for now. Let's take two A and B. We see them ''in sync'' i.e. they move in sync from one side to the other. You're right in that IF they're not in sync they'll move out of phase after ''some time''. This seems quite obvious if the periods (time taken to make one swing) are whole numbers. For instance, if A's is 2 seconds and B's is 3 seconds it becomes quite obvious that they're out of sync.
However, what if A's is 2.000000009 seconds and B's is 2.0000000000000009 seconds? This imperciptible difference will compound over time and after, may be millions of years, A and B will be out of sync.
Another thing is the assumption (is there a physics law for this?) that the pendulum swing will remain constant. We can't be sure of that without using another time piece and we're back to the chicken-egg problem.
Welcome to The Philosophy Forum!
Get involved in philosophical discussions about knowledge, truth, language, consciousness, science, politics, religion, logic and mathematics, art, history, and lots more. No ads, no clutter, and very little agreement — just fascinating conversations.
Categories
- Guest category
- Phil. Writing Challenge - June 2025
- The Lounge
- General Philosophy
- Metaphysics & Epistemology
- Philosophy of Mind
- Ethics
- Political Philosophy
- Philosophy of Art
- Logic & Philosophy of Mathematics
- Philosophy of Religion
- Philosophy of Science
- Philosophy of Language
- Interesting Stuff
- Politics and Current Affairs
- Humanities and Social Sciences
- Science and Technology
- Non-English Discussion
- German Discussion
- Spanish Discussion
- Learning Centre
- Resources
- Books and Papers
- Reading groups
- Questions
- Guest Speakers
- David Pearce
- Massimo Pigliucci
- Debates
- Debate Proposals
- Debate Discussion
- Feedback
- Article submissions
- About TPF
- Help
More Discussions
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum






