-
 frank
18.7k
frank
18.7k
The 3,4,5 probably came from a technique for building structures that have 90 degree angles. The basis for the Pythagorean Theorem is a practical "trick." I'm guessing the path from the trick to the theorem just came from playing with the components. Right? -
 Andrew M
1.6kThe 3,4,5 probably came from a technique for building structures that have 90 degree angles. — frank
Andrew M
1.6kThe 3,4,5 probably came from a technique for building structures that have 90 degree angles. — frank
The Pythagorean Theorem is also useful for visualizing relativistic spacetime.
Consider the twin paradox. Suppose Alice stays at home in lockdown for a year while Bob evades lockdown and travels a round-trip distance of 0.6 light years (6 trillion kilometers). How much older is Bob when he returns (at the end of Alice's year in lockdown)?
Both Alice and Bob travel over the same length of spacetime. However Bob trades off some time for the space that he has traveled. This trade-off is visually represented by a right-angled triangle, like so:
" /| Alice's elapsed time = / | Bob's elapsed time? 1 year / | √(1^2 - 0.6^2) = / | 0.8 years (9.6 months) ------ Bob's travel distance = 0.6 light years (in Alice's reference frame) "
But which came first: the idea or the visualization? — frank
Sometimes the visualization comes later than the idea. For example, the rotational picture for complex numbers came later:
That this subject [imaginary numbers] has hitherto been surrounded by mysterious obscurity, is to be attributed largely to an ill adapted notation. If, for example, +1, -1, and the square root of -1 had been called direct, inverse and lateral units, instead of positive, negative and imaginary (or even impossible), such an obscurity would have been out of the question. — Carl Friedrich Gauss -
 Gnomon
4.3k
Gnomon
4.3k
Unfortunately, the link has been taken down. But as an Architect, I'm familiar with the "practical trick", as Frank called it. For those interested in the pre-Pythagorean history of the theorem, Howard Bloom goes into extravagant detail on how the pragmatic rule-of-thumb was used long before anyone developed a theory to explain it mathematically, or to interpret its magic spiritually, or to build a mathematics cult upon its foundation.But which came first: the idea or the visualization? — frank
The God Problem by Howard Bloom : 3. The Sorcery of Corners.
"It's called the pattern of Pythagorean triples . . . the powers of these triples are so close to summoning spirits from the ether that it's ridiculous".
https://www.amazon.com/God-Problem-Godless-Cosmos-Creates/dp/1633881423 -
 Andrew M
1.6kWow! So an idea can interfere with visualization? Change your ideas and new doors open for visualization? — frank
Andrew M
1.6kWow! So an idea can interfere with visualization? Change your ideas and new doors open for visualization? — frank
In the case of complex numbers, the idea was sound but there was initially no visualization. It was just a technique that allowed mathematicians to solve special types of cubic equations but seemed otherwise mysterious.
Whereas the geometric interpretation provides insight. For example, Euler's identity
can be visualized by subtracting 1 from both sides. Then -1 is equivalent to starting with 1 and growing laterally at a rate of pi. -
 Gregory
5kEuclids 7th prop first book is a key to understanding this i think, although I don't understand his proof perfectly. The PT seems to work only when the right sides are seen to have a finite length greater than one 1. Of course they can be seen to be uncountably measured but that gets into the Cantor mire. My point is when you have "1 times one equals one" in a geometrical equation it doesn't make sense. So maybe the PT is even wrong when the rights sides are seen as one foot long
Gregory
5kEuclids 7th prop first book is a key to understanding this i think, although I don't understand his proof perfectly. The PT seems to work only when the right sides are seen to have a finite length greater than one 1. Of course they can be seen to be uncountably measured but that gets into the Cantor mire. My point is when you have "1 times one equals one" in a geometrical equation it doesn't make sense. So maybe the PT is even wrong when the rights sides are seen as one foot long -
 InPitzotl
880Thought you'd like this — frank
InPitzotl
880Thought you'd like this — frank
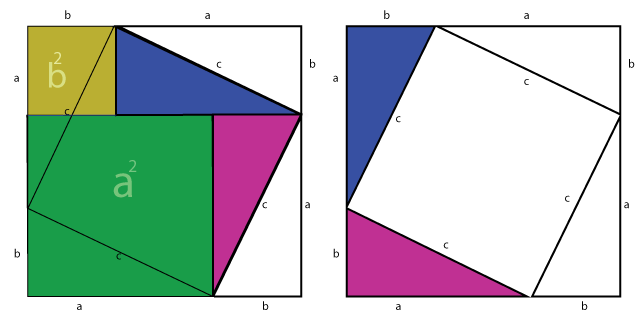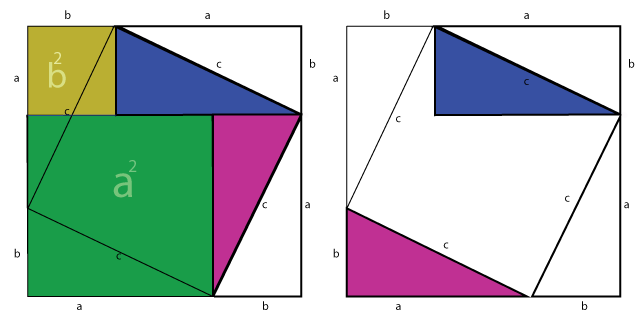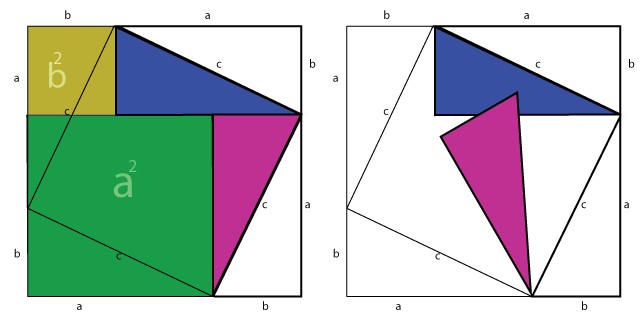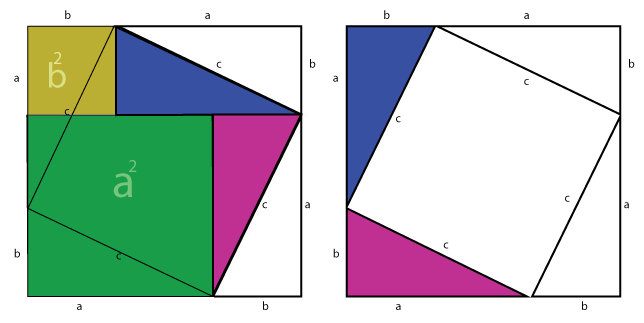
This visual proof is a bit more elegant:
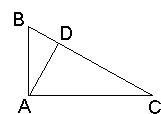
http://www.cut-the-knot.org/pythagoras#6
Simple version of proof: Given ABC with A as a right angle, construct its altitude AD. ABD, ADC, and ABC are all similar. Visually, the area of ABC=the area of ABD+ADC. Now picture ABD as a shape extending from AB, ADC as a similar shape extending from AC, and ABC as a similar shape extending from BC, and we have established that in this particular case, the area of two similar shapes extending from the sides equals the area of a similar shape extending from the hypotenuse. One can show that if this is true for one shape it's true for any shape ("exercise left to the reader"), thus it's true for squares, thus AB^2+AC^2=BC^2. -
 Gnomon
4.3kHow is 3,4,5 divine? — frank
Gnomon
4.3kHow is 3,4,5 divine? — frank
Thag's Cult : Numbers, Pythagoras believed, were the elements behind the entire universe. He taught his followers that the world was controlled by mathematical harmonies that made up every part of reality. More than that, though, these numbers were sacred—almost like gods.
https://listverse.com/2017/04/26/10-strange-facts-about-pythagoras-mathematician-and-cult-leader/ -
 frank
18.7k
frank
18.7k
Could you guys share your philosophy of math with me? Specifically, is the beer of math made of practical problems and tricks with an emergent foam of ideas?
Or are ideas actually fundamental, like gods in the stratosphere, and practicalities are down here dimly reflecting those perfections? -
 EnPassant
699Could you guys share your philosophy of math with me? — frank
EnPassant
699Could you guys share your philosophy of math with me? — frank
Numbers and the relationships between them are eternal truths. I'm sure God is aware of this. But math for God must be way beyond what we would even conceive of as math.
It is easy to create numbers.
Start with "/"
Iterate "//"
Reiterate "///"
etc "//////////////////..."
Partition each step:
/, //, ///,...
= 1, 2, 3,...
I'm sure God worked out this long before anyone else.
Once numbers exist mathematics (especially The Theory of Numbers) exists.
And once that exists, complexity exists.
Therefore God can be complex in terms of the contemplation of numbers.
And this answers Dawkins' assertion that God cannot be complex without a creator.
He can be complex by way of knowledge.
And once all this exists it is a matter of putting 'meat' on the abstract bones of mathematics.
Experience of reality in ordinary terms can awaken in our consciousness the mathematical order of reality because the world is intrinsically mathematical anyhow: induction awakens our powers of deduction. That, I think, is a big part of how science works. -
 frank
18.7kThat's actually a beautiful picture of things. I think it leads to a problem of evil though. Do you have a solution?
frank
18.7kThat's actually a beautiful picture of things. I think it leads to a problem of evil though. Do you have a solution? -
 EnPassant
699That's actually a beautiful picture of things. I think it leads to a problem of evil though. Do you have a solution? — frank
EnPassant
699That's actually a beautiful picture of things. I think it leads to a problem of evil though. Do you have a solution? — frank
Thank you. Because good (being) exists, distortions of good exist. As St. Augustine said, evil is not a positive thing in itself. It is a lack of the good. The good is a perfect symphony. Evil is disharmony. But evil cannot exist without the good, without being, which is God. -
 Andrew M
1.6kCould you guys share your philosophy of math with me? — frank
Andrew M
1.6kCould you guys share your philosophy of math with me? — frank
Aristotelian realism. The world has a mathematical structure (form) that we can investigate.
The essay that @Wayfarer highlighted in the Aristotle thread is a good summary. It even mentions visualization:
Our developed human intellectual abilities add two things to those simple perceptions. The first is visualisation, which allows us to understand necessary relations between mathematical facts. Try this easy mental exercise: imagine six crosses arranged in two rows of three crosses each, one row directly above the other. I can equally imagine the same six crosses as three columns of two each. Therefore 2 × 3 = 3 × 2. I not only notice that 2 × 3 is in fact equal to 3 × 2, I understand why 2 × 3 must equal 3 × 2. — The mathematical world - James Franklin -
 EnPassant
699imagine six crosses arranged in two rows of three crosses each, one row directly above the other. I can equally imagine the same six crosses as three columns of two each. Therefore 2 × 3 = 3 × 2. I not only notice that 2 × 3 is in fact equal to 3 × 2, I understand why 2 × 3 must equal 3 × 2. — The mathematical world - James Franklin
EnPassant
699imagine six crosses arranged in two rows of three crosses each, one row directly above the other. I can equally imagine the same six crosses as three columns of two each. Therefore 2 × 3 = 3 × 2. I not only notice that 2 × 3 is in fact equal to 3 × 2, I understand why 2 × 3 must equal 3 × 2. — The mathematical world - James Franklin
This is an example of induction (observation) awakening our powers of deduction. Resulting in deducing the commutative nature of multiplication: 2 x 3 = 3 x 2. -
 Benkei
8.1kAt least in the android store. Don't know about iPhone. They also made euclidea and pythagoras but those are two dimensional. That last one had really bad English though.
Benkei
8.1kAt least in the android store. Don't know about iPhone. They also made euclidea and pythagoras but those are two dimensional. That last one had really bad English though. -
 talminator2856791
3Probably came from algebra x2 + y2 = z2
talminator2856791
3Probably came from algebra x2 + y2 = z2
32 + 42 = 52 — EnPassant
yes but that needs a proof to show that x^2 + y^2 = z^2. it needs a reason. however it could have been an observation, but not all x, y and z can satisfy this property for natural numbers. so most likely it was an observation, then the proof/reason came about for any x, y and z that satisfy. and there are many proofs for pythagoras, some are visual and some more algebraic or concrete and some are even just bi-products or specific cases of different ideas. a good example of that is ptolemy's theorem. ptolemy's theorem is more general than pythagoras theorem. it is the general case for any cyclic quadrilateral and pythagoras is just one of the infinitely many cases. -
 EnPassant
699ptolemy's theorem — talminator2856791
EnPassant
699ptolemy's theorem — talminator2856791
I had not heard of that. Very interesting. The Greeks did math by geometry so they may have discovered it geometrically first and then did the algebra.
Welcome to The Philosophy Forum!
Get involved in philosophical discussions about knowledge, truth, language, consciousness, science, politics, religion, logic and mathematics, art, history, and lots more. No ads, no clutter, and very little agreement — just fascinating conversations.
Categories
- Guest category
- Phil. Writing Challenge - June 2025
- The Lounge
- General Philosophy
- Metaphysics & Epistemology
- Philosophy of Mind
- Ethics
- Political Philosophy
- Philosophy of Art
- Logic & Philosophy of Mathematics
- Philosophy of Religion
- Philosophy of Science
- Philosophy of Language
- Interesting Stuff
- Politics and Current Affairs
- Humanities and Social Sciences
- Science and Technology
- Non-English Discussion
- German Discussion
- Spanish Discussion
- Learning Centre
- Resources
- Books and Papers
- Reading groups
- Questions
- Guest Speakers
- David Pearce
- Massimo Pigliucci
- Debates
- Debate Proposals
- Debate Discussion
- Feedback
- Article submissions
- About TPF
- Help
More Discussions
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum