-
 Wheatley
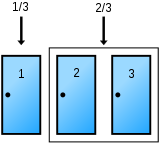
2.3kFor those who don't know, the Monty Hall problem involves a game show where there are three doors. One of them contains a car, the other two contain a goat. You get to choose any door you want. You also get to keep whatever is behind that door. So if you pick a goat, you get a goat. And if you pick the car, you get the car. You want to pick the car because it's worth more.
Wheatley
2.3kFor those who don't know, the Monty Hall problem involves a game show where there are three doors. One of them contains a car, the other two contain a goat. You get to choose any door you want. You also get to keep whatever is behind that door. So if you pick a goat, you get a goat. And if you pick the car, you get the car. You want to pick the car because it's worth more.
You don't know what is in what door, but you choose to pick door 1. The game show host knows which doors contain the goats, and opens door 2 to reveal a goat, and asks, "Do you want to stay with door 1, or do you want to switch to door 3?". Most people would stay with door 1 because they don't want to change their choice, and they also believe that chance of there being a car in door 1 is now 50/50. But mathematically, the contestant should switch to door 3 because it's 2/3 more likely that door has the car. That, in a nutshell, is the Monty Hall problem.
Now suppose you happen to have a program that can simulate the Monty Hall game show. You run the program, and the graphics show three doors, two of which has a goat behind them, one of which has a car. The program simulates the game show, but with a variation, the program doesn't know behind which door the goats are, nor the car. At the beginning of the game, like the original Monty hall show, the user is given a choice to click on one of the three doors. However, unlike the original Monty Hall show, the computer picks one of the other two doors at random to open. This time, it may contain a goat, or it may contain the car.
And here's the crucial part. If the computer, who randomly opens one of the other two doors you didn't choose, reveals the car, the program terminates right there, and starts again. If on the other hand, the computer opens one of the other doors, and by chance it is a goat, the program continues and you are given a choice to switch or not.
My question is, in this simulation of the Monty Hall show, with this extra random variation where the computer doesn't "know" which door contains the goat or car, but reveals a goat in one of the other doors by chance, is the probability still 2/3 that the other unopened door contains the car? Or does the probability change because of the extra random process? -
 Hanover
15.1kI don't see how your variation changes the odds. The issue isn't the foreknowledge of the host, but of the knowledge of the contestant as revealed by the host. The way you've set this up, if I'm understanding correctly, is that you have a contestant who chose door #1, then another door is revealed to him that does not contain the car, and then you ask whether he should change doors. Just as in the initial case, the answer is yes. My understanding is that you disregard those instances where the computer chooses and shows the car or the goat, so they really aren't being included in your decision making.
Hanover
15.1kI don't see how your variation changes the odds. The issue isn't the foreknowledge of the host, but of the knowledge of the contestant as revealed by the host. The way you've set this up, if I'm understanding correctly, is that you have a contestant who chose door #1, then another door is revealed to him that does not contain the car, and then you ask whether he should change doors. Just as in the initial case, the answer is yes. My understanding is that you disregard those instances where the computer chooses and shows the car or the goat, so they really aren't being included in your decision making. -
 Echarmion
2.7kI'm not saying this is incorrect, but some people try to explain the Monty Hall problem in terms of what the host knows and has to reveal. — Purple Pond
Echarmion
2.7kI'm not saying this is incorrect, but some people try to explain the Monty Hall problem in terms of what the host knows and has to reveal. — Purple Pond
And that is relevant, because the reason you are getting additional information out of the host's decision is that this decision follows a predetermined rule.
You have recreated that rule though, by having the game terminate. If the game does not terminate, the player gains information.
Edit: the Monty Hall problem can always be solved with a decision tree. There is still a 2/3 chance to initially select the wrong door, and if you did, then you should switch if one wrong door is subsequently eliminated. -
 unenlightened
10kThe best way to make it intuitive is to add more doors. So - 100 doors, 99 goats, you choose a door, then Monty chooses 98. There's going to be a lot of abandoned games in this scenario. But eventually you arrive at the two doors one of which has the car. In effect you have chosen one and Monty the other from a position of equal ignorance. Monty is not more likely to be correct than you.
unenlightened
10kThe best way to make it intuitive is to add more doors. So - 100 doors, 99 goats, you choose a door, then Monty chooses 98. There's going to be a lot of abandoned games in this scenario. But eventually you arrive at the two doors one of which has the car. In effect you have chosen one and Monty the other from a position of equal ignorance. Monty is not more likely to be correct than you.
Compare this with the same game where Monty knows where the car is: Monty always picks the door with the car to leave, except the 1 in 100 where you have picked it. -
 Michael
16.6kMy question is, in this simulation of the Monty Hall show, with this extra random variation where the computer doesn't "know" which door contains the goat or car, but reveals a goat in one of the other doors by chance, is the probability still 2/3 that the other unopened door contains the car? Or does the probability change because of the extra random process? — Purple Pond
Michael
16.6kMy question is, in this simulation of the Monty Hall show, with this extra random variation where the computer doesn't "know" which door contains the goat or car, but reveals a goat in one of the other doors by chance, is the probability still 2/3 that the other unopened door contains the car? Or does the probability change because of the extra random process? — Purple Pond
Still 2/3. The door you chose retains the initial 1/3 chance and the other door must have a 1 - 1/3 chance, i.e. 2/3. -
TheMadFool
13.8kAnd here's the crucial part. If the computer, who randomly opens one of the other two doors you didn't choose, reveals the car, the program terminates right there, and starts again. If on the other hand, the computer opens one of the other doors, and by chance it is a goat, the program continues and you are given a choice to switch or not. — Purple Pond
Switch because the computer didn't shut down???!!! :chin: -
 Michael
16.6kAgain - why are you biasing in favour of one door?
Michael
16.6kAgain - why are you biasing in favour of one door?
The goat likewise raises the probability of door 1. — Shamshir
If we play the game 99 times with 3 doors then we'd expect our initial selection to be right 33 times because the car has an equal chance of being behind each of doors 1, 2, and 3, so we can't win more than 33 games (out of 99) by not switching. -
 Michael
16.6kStill 2/3. The door you chose retains the initial 1/3 chance and the other door must have a 1 - 1/3 chance, i.e. 2/3. — Michael
Michael
16.6kStill 2/3. The door you chose retains the initial 1/3 chance and the other door must have a 1 - 1/3 chance, i.e. 2/3. — Michael
I've changed my opinion on this after running some simulations. Unless I'm doing it wrong, there's a 43% chance of winning by not switching and a 57% chance of winning by switching.
There is a difference between the OP's version of the game and the original. In the original you would expect your initial door to contain the car 33 times out of every 99 games you're asked to switch. However, in the OP's version of the game you're not asked to switch every game; some games are ended early. My simulations suggest that 22% of games end early.
So it's still better to switch, just not as better. -
 Wheatley
2.3kI don't think the initial probability of picking a car at a random door is 1/3. Think about it. Consider you pick door 1, there are 3 possibilities:
Wheatley
2.3kI don't think the initial probability of picking a car at a random door is 1/3. Think about it. Consider you pick door 1, there are 3 possibilities:
Door 1 has the car. Program doesn't restart.
Door 1 has a goat, Program opens door 2, and it's a goat. Program doesn't restart.
Door 1 has a goat, Program opens door 3, and it's the car. Program restarts.
So 1/2 times you pick the goat in the door you choose, the computer invalidates that decision, and restarts. It's like you are given an extra chance. -
 Michael
16.6kOne door has zero chance and chances are split to 1/2.
Michael
16.6kOne door has zero chance and chances are split to 1/2.
Where's the indication that one door is more likely, assumptions that one chose wrong aside? — Shamshir
There are 3 unnumbered doors. I pick one at random. That door is then numbered "1". The left-most of the remaining doors is numbered "2" and the other numbered "3". A door is selected at random and a car placed behind it. If we play 99 games then 33 times the door is behind door "1" (my door), 33 times the door is behind door "2", and 33 times the door is behind door "3".
If I don't switch then I win 33 times. If I switch then I win 66 times (if we're playing the standard game; as my post above explains, the situation is slightly different with the OP's variation, although it's still better to switch). -
 Shamshir
855But one door has zero probability and the remaining two are equiprobable.
Shamshir
855But one door has zero probability and the remaining two are equiprobable.
In theory the chances are 50/50 from beginning to end as the revealed dud is nonfactor; it only appears to be 2/3 if you focus on the dud with the assumption that you chose wrong, if you assume you chose right vice versa.
In practice, you might not win one game by switching. -
 Michael
16.6kBut one door has zero probability and the remaining two are equiprobable.
Michael
16.6kBut one door has zero probability and the remaining two are equiprobable.
In theory the chances are 50/50 from beginning to end as the revealed dud is nonfactor; it only appears to be 2/3 if you focus on the dud with the assumption that you chose wrong, if you assume you chose right vice versa. — Shamshir
Forget about Monty opening a door and just look at the initial selection where I have to pick from doors 1, 2, or 3. If we play 99 games then that first selection will be right 33 times, so I can't win more than 33 games by not switching. Monty opening a door can't make it that I can win 50 games by not switching.
In practice, you might not win one game by switching.
And you might not win one game by not switching. But we're discussing probability theory here. -
 Shamshir
855But you practically can, you can win all 99 by not switching.
Shamshir
855But you practically can, you can win all 99 by not switching.
Without the assumption that you chose wrong, the three doors are equiprobable - and staying or switching you would win 33 games anyway, by the posited logic.
If we simply choose one and reveal them all it's 1/3.
If we remove the dud from the equation, it should be obvious you're limited to two options and it's 1/2.
If we by condition of the dud, assume we chose wrong, then yes, you can skew the chances to 2/3. -
 Michael
16.6kBut you practically can, you can win all 99 by not switching. — Shamshir
Michael
16.6kBut you practically can, you can win all 99 by not switching. — Shamshir
You can win all 99 by switching as well.
Without the assumption that you chose wrong, the three doors are equiprobable - and staying or switching you would win 33 games anyway, by the posited logic. — Shamshir
That's not right. Probability dictates that if we play 99 games then I am likely to pick the correct door 33 times. That means that I will win 33 games and lose 66 games by not switching, and so therefore win 66 games and lose 33 games by switching. -
 Michael
16.6kIf we simply choose one and reveal them all it's 1/3.
Michael
16.6kIf we simply choose one and reveal them all it's 1/3.
If we remove the dud from the equation, it should be obvious you're limited to two options and it's 1/2.
If we by condition of the dud, assume we chose wrong, then yes, you can skew the chances to 2/3. — Shamshir
33 times the car is behind "my door".
33 times the car is behind "other door 1".
33 times the car is behind "other door 2".
If I don't switch then I will win 33 times when the car is behind "my door", 0 times when the car is behind "other door 1", and 0 times when the car is behind "other door 2". My win rate is 33/99 = 1/3.
If I switch then I will win 0 times when the car is behind "my door", 33 times when the car is behind "other door 1", and 33 times when the car is behind "other door 2". My win rate is 66/99 = 2/3.
66 times out of 99 games we're being asked if we want to switch to the winning door. -
 Echarmion
2.7kI don't think the initial probability of picking a random door is 1/3. Think about it. — Purple Pond
Echarmion
2.7kI don't think the initial probability of picking a random door is 1/3. Think about it. — Purple Pond
Doesn't "initial probability" mean irrespective of all later factors? In which case I don't see how it could be anything but 1/3. -
 unenlightened
10kMy door. C______G_____G
unenlightened
10kMy door. C______G_____G
Monty's G_G___C_G___C_G
Six permutations, but the combination G+G is eliminated by the exposure of the car, as indicated above by the invisible strikes. One game in three my door wins, one game in three Monty's door wins, and one game in three is abandoned. So it's even odds.
In the original problem, the combination G+G is avoided by Monty's choice; no games are abandoned Monty's odds are doubled. -
 Michael
16.6kSix permutations, but the combination G+G is eliminated by the exposure of the car, as indicated above by the invisible strikes. One game in three my door wins, one game in three Monty's door wins, and one game in three is abandoned. So it's even odds. — unenlightened
Michael
16.6kSix permutations, but the combination G+G is eliminated by the exposure of the car, as indicated above by the invisible strikes. One game in three my door wins, one game in three Monty's door wins, and one game in three is abandoned. So it's even odds. — unenlightened
I don't think that's right.
There's a 1/2 chance that he picks door 2 and a 1/2 chance that he picks door 3.
There's a 1/3 chance that the car is behind door 2 and a 1/3 chance that the car is behind door 3.
What is the chance that the car is behind the door he picks? 1/2 * 1/3 = 1/6. So of 99 games, ~17 are abandoned. Therefore 82 games are played to completion.
In 33 of those games the car is behind door 1 (my door). If I don't switch then I win 33/82 = 40% and if I do switch then I win 49/82 = 60%. This is pretty close to what my simulations showed (I'll look into why they're not exact). -
 Michael
16.6k
Michael
16.6k -
 Echarmion
2.7k
Echarmion
2.7k
I think I get it too now. If I get the option to switch, that means the game didn't restart. It's less likely I picked the right door initially. But, given that the game did not restart, it becomes more likely that I picked the right door. Not sure exactly how the mathematical operation looks though.
Monty hall problems are apparently difficult even if you know the basics. -
 Michael
16.6kI think I get it too now. If I get the option to switch, that means the game didn't restart. It's less likely I picked the right door initially. But, given that the game did not restart, it becomes more likely that I picked the right door. Not sure exactly how the mathematical operation looks though.
Michael
16.6kI think I get it too now. If I get the option to switch, that means the game didn't restart. It's less likely I picked the right door initially. But, given that the game did not restart, it becomes more likely that I picked the right door. Not sure exactly how the mathematical operation looks though.
Monty hall problems are apparently difficult even if you know the basics. — Echarmion
If we're playing 99 games then in 33 games the car is behind my door, in 33 games the car is behind the door the computer picks, and in 33 games the car is behind the door the computer doesn't pick. The 33 games where the car is behind the door the computer picks are dismissed so I'm only ever asked to switch in 66 games; 33 in which the car is behind my door and 33 in which the car is behind the door the computer doesn't pick. -
 unenlightened
10kSo there's a game on uk telly called 'Who wants to be a millionaire. A series of questions with 4 possible answers A, B, C, D. On one question, you can ask the computer to remove two wrong answers at random. So you take a guess in your mind - say 'A'. Then the computer takes away - say B and C, leaving A and D. Is there any reason to switch to D?
unenlightened
10kSo there's a game on uk telly called 'Who wants to be a millionaire. A series of questions with 4 possible answers A, B, C, D. On one question, you can ask the computer to remove two wrong answers at random. So you take a guess in your mind - say 'A'. Then the computer takes away - say B and C, leaving A and D. Is there any reason to switch to D? -
 Michael
16.6kNo, because the computer could have removed your guess (if it’s wrong), and so the logic isn’t comparable to the Monty Hall problem.
Michael
16.6kNo, because the computer could have removed your guess (if it’s wrong), and so the logic isn’t comparable to the Monty Hall problem.
Welcome to The Philosophy Forum!
Get involved in philosophical discussions about knowledge, truth, language, consciousness, science, politics, religion, logic and mathematics, art, history, and lots more. No ads, no clutter, and very little agreement — just fascinating conversations.
Categories
- Guest category
- Phil. Writing Challenge - June 2025
- The Lounge
- General Philosophy
- Metaphysics & Epistemology
- Philosophy of Mind
- Ethics
- Political Philosophy
- Philosophy of Art
- Logic & Philosophy of Mathematics
- Philosophy of Religion
- Philosophy of Science
- Philosophy of Language
- Interesting Stuff
- Politics and Current Affairs
- Humanities and Social Sciences
- Science and Technology
- Non-English Discussion
- German Discussion
- Spanish Discussion
- Learning Centre
- Resources
- Books and Papers
- Reading groups
- Questions
- Guest Speakers
- David Pearce
- Massimo Pigliucci
- Debates
- Debate Proposals
- Debate Discussion
- Feedback
- Article submissions
- About TPF
- Help
More Discussions
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum