-
 Perplexed
70I'm not sure your answer is convincing because we do not only keep maths that has practical utility. It need only be internally coherent and can be built up deductively using the rules we put into it. It could be many years later that a practical utility is found for a system that was initially believed to be only a mathematical curiosity.
Perplexed
70I'm not sure your answer is convincing because we do not only keep maths that has practical utility. It need only be internally coherent and can be built up deductively using the rules we put into it. It could be many years later that a practical utility is found for a system that was initially believed to be only a mathematical curiosity. -
 Agustino
11.2k
Agustino
11.2k
Yes, this is exactly what I'm saying. I'm a bit uneasy about your use of "intuition" there though.It's as if you're saying non-euclidian a posteriori discoveries are true and a priori euclidian intuitions are false. — Hanover
Alas - if a so-called a priori claims something that contradicts what an a posteriori reveals, then obviously the latter is true, and the former is false. You cannot have two contradictory statements hold as true with regards to the same subject matter at the same time.
I don't understand the question?How do you know which is true when truth is noumenal? — Hanover
A posteriori experience, and physical experiments are also phenomenal. They investigate the phenomenon, by no means do they investigate the noumenon. A posteriori non-euclidean statements hold with regards to the phenomenon. According to Kant's definitions at least.All we're talking about is phenomenal, and it's perfectly logical to say that euclidian intuitions are necessary for phenomenal experience even if a posteriori knowledge might be discovered that is incomprehensible on an intuitive level. — Hanover -
 Agustino
11.2k
Agustino
11.2k
Sure, but we build by building on what exists before, trying to make it more general, and extend it. Like the factorial situation. We don't have negative factorials, so we try to find a way to have negative factorials that is in agreement with what we already have.It need only be internally coherent and can be built up deductively using the rules we put into it. It could be many years later that a practical utility is found for a system that was initially believed to be only a mathematical curiosity. — Perplexed -
 Moliere
6.5kOi. Well, the questions got specific enough that I felt a need to review. So far I've just been relying upon memory, which is far from faultless but a hell of a lot quicker when it comes to responding. :D
Moliere
6.5kOi. Well, the questions got specific enough that I felt a need to review. So far I've just been relying upon memory, which is far from faultless but a hell of a lot quicker when it comes to responding. :D
Thus far I've read these two articles to remind me of the finer points of the aesthetic -- though I am fine with cracking open the source material too if we need to. Regardless, these are both pretty darn good articles to read with respect to the original question:
https://plato.stanford.edu/entries/kant-mathematics/
https://plato.stanford.edu/entries/kant-spacetime/
@Janus and @Perplexed too for the above articles, though the rest of this is directed at Agustino.
On what grounds do we judge a geometrical proposition to be a synthetic a priori? — Agustino
After reading the above articles I might make a modification, actually. I'm sort of toying between two ideas. Originally my thought was that any geometry upon which natural phenomena are predicted would count as the synthetic a priori geometry, whereas previous geometries would be considered approximations of the a priori -- and therefore empirical, since they are no longer necessary (at least for predicting physical phenomena occuring within the forms of space and time).
But now I'm wondering if it's possible that both could be considered synthetic a priori -- since we can demonstrate either geometry within the non-empirical intuition by means of either physics. It would still count as a cognition regardless of the physics we use.
(1) Why is it sensible that we could be wrong about the form of the intuition?
"Sensible" as in why does it make sense and is reasonable?
If so, then it would just be a matter of the fact that propositions are truth-apt. We can say "All intuitions are empirical", and that would be false (via Kant, at least). There is a subject, "is", and a predicate, and the category of "Allness" appended so it fits within the logic of Kant. And surely it is truth-apt, since Kant argues against the truth of the proposition.
(2) Does the form of intuition belong to our subjectivity? If so, is it possible to be wrong about our own subjectivity?
Yes and yes.
"Subjectivity" understood within the context of Kantian philosophy, of course. Definitely a tricky word, but yes and yes.
(3) Can we know whether a geometric statement really is a synthetic a priori with certainty? And if so, how?
Well, toying with the two ideas I talked of above...
My first inclination was to say that any geometry upon which the physical sciences rests would count as the synthetic a priori geometry, and would thereby be certain.
But now I'd also note that certainty isn't quite as important in Kant as other epistemologies. Certainty is obtained subjectively or objectively -- and the difference between the two is subjective certainty is where one person holds something to be true, and objective certainty is when everyone does. I had to look up certainty in A Kant Dictionary to come up with that, though. It's by Howard Caygill, and just like the above articles certainly relies upon a certain interpretation to help readers through Kant -- but unfortunately I didn't mark in my CPR where Kant talks about the conditions of certainty :D. So I found it hard to find.
I don't follow how "we are able to have synthetic a priori knowledge about space due to our knowledge of geometry". Our synthetic a priori knowledge of space is what we codify through geometry.
I'd very much disagree with this assertion. Though space is the form of outer intuition, and is so for everyone with an intellect like ours, knowledge cannot be obtained except by the use of both our understanding and intuition. Space is an intuition, and knowledge of space only comes about by use of the understanding.
I also don't follow what you mean by "space isn't intuitively obvious to us". For example, it seems impossible to imagine 4D space. So is the three-dimensionality of space not something intuitively obvious to us? Could we be wrong about that too? And what would that even mean?
Eh, bit of a side issue, but I would say that 3D space is not intuitively obvious to us.
Regardless, though, "intuition" is not the same as "intuitive" -- "intuition" is one half of the mind which operates differently from understanding, where "intuitive" is more akin to meaning obvious or easily comprehended without instruction or something along those lines.
My main point here is that "intuition" does not mean the same thing as "intuitive", and that is an understandable mistake, but a mistake all the same.
If I follow you correctly, your point is the traditional Kantian one that the phenomenal world is organised through the a priori forms of space and time and the categories of the understanding - so in this specific case, space doesn't exist "out there", it is just how we represent the phenomenal world to ourselves. In other words, space continues to be transcendentally ideal per your view?
More or less, yes. Not sure about "out there" in your reply, so I say "more or less", but everything else is what I'd say (that Kant says, at least).
So if we don't have synthetic a priori knowledge of the form of intuition there are two main questions:
??? I don't mean to imply we have no synthetic a priori knowledge. Is it of the form of intuition? I'm not sure because things get funny when we are looking at the frame (is it knowledge, at that point? Or simply what we must accept in order that knowledge be possible? Is it really a cognition anymore?). But mathematical knowledge relies upon the form of intuition.
(1) Since the form of intuition is subjective, why don't we have such knowledge? How does acting in the world (empiricism, scientific experiments, etc.) help us gain that knowledge? Aren't we ultimately gaining knowledge about ourselves then?
We do have that knowledge. The way that acting in the world helps us gain the knowledge is that we compare concepts to our intuitions, and the form of intuition is the basis for geometry. In a way you could argue we are learning about ourselves, but in a way that also doesn't make sense to say -- because it's not really about our identity or psychology but rather the possibility of knowledge.
(2) How do we even know that synthetic a priori knowledge even exists if we do not know when we have it? How can we know if a piece of synthetic knowledge is a priori (Riemmann) or a posteriori (Euclidean)?
I think in the above I answered these. Let me know if you disagree. -
 Moliere
6.5kI still don't have a lot of time, so since you think this might be the salient point of our disagreement, we probably should focus on defining our terms and thereby hopefully gaining enough confluence to progress the discussion.
Moliere
6.5kI still don't have a lot of time, so since you think this might be the salient point of our disagreement, we probably should focus on defining our terms and thereby hopefully gaining enough confluence to progress the discussion.
"Thoughts without content are empty, intuitions without concepts are blind." This well-worn quotation form Kant I have always taken to be suitably paraphrased as " Conceptions without perceptual content are empty, perceptions without conceptual content are blind". — Janus
No worries about time. As you see I can take a bit of time to respond too. (sometimes too much time! Sometimes I run out of ideas, too...) Take as much time as you need.
I don't think your paraphrase is off. I also don't think the well-worn quotation is Kant at his most rigorous. I think perception is a good stepping-stone for getting a handle on the critical philosophy, but when speaking strictly I'd caution against thinking of intuition as perception. Intuition is just one half of the mind which acts entirely differently from the other half of the mind -- the understanding.
Or, another way of putting this would be to say there's the understanding and sensibility, and intuition is a part of sensibility. I'm not sure which way to put it, myself.
In either rendition though perception is a psychological phenomena -- it deals with how a particular mind, and how many similarly wired particular minds, come(s) to recognize some phenomena as that phenomena.
But in the case of Kant we're dealing more with how all particular minds arranged Kant-wise (just to be cheeky -- I forget the exact term Kant uses, but our minds are contrasted with an intellectual intuition to give an idea of what sorts of mind he means {EDIT: and, just in case, an intellectual intuition is something like the mind of god, where thinking something creates reality -- not trying to talk down, just trying to make sure I cover my bases}) come to have knowledge about the world -- and in particular synthetic a priori knowledge. It's not about how we see a particular phenomena as that phenomena, but rather how it is possible for us to know some subject is attached to a predicate synthetically and without having to rely upon particular experience.
Linguistically -- perception's "link" is the word "as", and knowledge's "link" is the copula. -
 Moliere
6.5kBut if physical effects external to ourselves can be shown to influence the geometry of space, is this not fatal to the assumption that space is an a priori form of our intuition? — Perplexed
Moliere
6.5kBut if physical effects external to ourselves can be shown to influence the geometry of space, is this not fatal to the assumption that space is an a priori form of our intuition? — Perplexed
I don't think so. Specifically because since the physical effects are demonstrated then they already fall within the form of intuition. "outside us" is not something that relies upon our intuitive perception of space, but rather "outside" -- meaning the noumenal world -- is outside of all possible knowledge. If we demonstrate that space behaves in accordance with one or another geometry then I'm inclined to say either 1) we have determined the "correct" geometry which conforms with the intuition, or 2) that both geometries are "checked against" the form of intuition, and hence both count as knowledge. -
 Agustino
11.2k
Agustino
11.2kThanks, I had a quick look and will read in more depth soon.
This doesn't make sense. Either the geometry is a synthetic a priori, or it's not. It cannot merely "count" as a synthetic a priori at one point, and not at another. If it is a priori, then it is always a priori. We can, on the other hand, be mistaken about which geometry is the a priori geometry. And if we can be mistaken, I have to ask that you specify how we can know if we are mistaken about it. And the further question, how can we know that (the geometry we have) it is a priori? Because knowing that, would seem to require infinite time, since a particular geometry (like the Euclidean) can always prove in the future not to have been complete.Originally my thought was that any geometry upon which natural phenomena are predicted would count as the synthetic a priori geometry, whereas previous geometries would be considered approximations of the a priori -- and therefore empirical, since they are no longer necessary (at least for predicting physical phenomena occuring within the forms of space and time). — Moliere
This doesn't make much sense to me. Both geometries are contradictory to each other. Two contradictory statements cannot both be true, hence they cannot both be a priori, since a priori truths are necessary, and hence always true.But now I'm wondering if it's possible that both could be considered synthetic a priori -- since we can demonstrate either geometry within the non-empirical intuition by means of either physics. It would still count as a cognition regardless of the physics we use. — Moliere
Yes."Sensible" as in why does it make sense and is reasonable? — Moliere
Propositions may be truth-apt, but if something is true in an a priori fashion, then it follows that it cannot fail to be true, regardless of what happens in the world. Like "it is raining or it is not raining".If so, then it would just be a matter of the fact that propositions are truth-apt. — Moliere
Why? Why does the fact that physics "rests" (what does that even mean?) on it guarantee it certainty?My first inclination was to say that any geometry upon which the physical sciences rests would count as the synthetic a priori geometry, and would thereby be certain. — Moliere
Can you explain how you can be wrong about your own subjectivity, and what you mean by that idea?Yes and yes. — Moliere
I doubt this. Kant does talk about apodeictic certainty innumerable times with regards to mathematics. Part of the TA project, as far as I see it, is to secure where the certainty of mathematics comes from - and for Kant, it comes from the (synthetic) a priority of its propositions.But now I'd also note that certainty isn't quite as important in Kant as other epistemologies. Certainty is obtained subjectively or objectively -- and the difference between the two is subjective certainty is where one person holds something to be true, and objective certainty is when everyone does. I had to look up certainty in A Kant Dictionary to come up with that, though. It's by Howard Caygill, and just like the above articles certainly relies upon a certain interpretation to help readers through Kant -- but unfortunately I didn't mark in my CPR where Kant talks about the conditions of certainty :D. So I found it hard to find. — Moliere
Right, I definitely agree with you here. This is undoubtedly correct from a Kantian point of view. So then, our geometrical judgements (Euclidean geometry) can be wrong. What exactly is the relationship between the intuition and the understanding that causes us to be capable of forming wrong concepts based on the former?Though space is the form of outer intuition, and is so for everyone with an intellect like ours, knowledge cannot be obtained except by the use of both our understanding and intuition. Space is an intuition, and knowledge of space only comes about by use of the understanding. — Moliere
So, if space is transcendentally ideal, then there is no noumenal space, correct?More or less, yes. — Moliere
Ok.But mathematical knowledge relies upon the form of intuition. — Moliere
So why is it that it took so long for us to discover non-Euclidean geometry? According to this development of Kant, we gain knowledge by comparing our concepts with our intuition. Do you claim that, in our intuition, we knew that non-Euclidean geometry is possible? If we did, then why did it take so long for us to compare our concepts (Euclidean geometry) with our intuition, and find out that they were different?The way that acting in the world helps us gain the knowledge is that we compare concepts to our intuitions, and the form of intuition is the basis for geometry. — Moliere -
 Moliere
6.5kThis doesn't make sense. Either the geometry is a synthetic a priori, or it's not. It cannot merely "count" as a synthetic a priori at one point, and not at another. If it is a priori, then it is always a priori. — Agustino
Moliere
6.5kThis doesn't make sense. Either the geometry is a synthetic a priori, or it's not. It cannot merely "count" as a synthetic a priori at one point, and not at another. If it is a priori, then it is always a priori. — Agustino
Yes, true. I just mean how we categorize something, not what it is.
We can, on the other hand, be mistaken about which geometry is the a priori geometry. And if we can be mistaken, I have to ask that you specify how we can know if we are mistaken about it. And the further question, how can we know that (the geometry we have) it is a priori? Because knowing that, would seem to require infinite time, since a particular geometry (like the Euclidean) can always prove in the future not to have been complete.
Well, it's a priori because it does not rely upon particular experience -- it is non-empirical. Space itself is classified as non-empirical. We don't come to know it through inference. Space, like time, is unique in this way: that it is both part of our intuition, and that it is non-empirical.
So it would seem to me that any geometry should at least count as a priori simply because it's not something we come to by way of inferring from experience but is seated in the understanding, first.
What then makes it synthetic is that the propositions of geometry rely upon more than the principle of non-contradiction. There is something added to the subject. And how we do that, as humans, is through the understanding being used to judge our form of intuition (in the case of geometric propositions, that is)
What makes it knowledge is that we then compare our propositions generated in the understanding to the form of intuition. And since it is knowledge of the form of intuition it is also universal and necessary.
And it's that fact that the very form of our intuition is what we are coming to know which then guarantees certainty of how objects relate to one another and also how they react. Since it is the form of our intuition that we are learning about it applies to everything within that form. Hence we can also be certain of our knowledge.
Whether some set of propositions is incomplete doesn't really influence whether or not it is a priori. And it is fair to say that Euclidean geometry is an approximation of space, if we are to take non-Euclidean geometry as the sort of true representation of space. Newtonian mechanics, after all, still work within certain parameters -- we just weren't always aware of what those parameters were.
This doesn't make much sense to me. Both geometries are contradictory to each other. Two contradictory statements cannot both be true, hence they cannot both be a priori, since a priori truths are necessary, and hence always true. — Agustino
What is contradictory in them? Perhaps we are wrong in thinking that.
Propositions may be truth-apt, but if something is true in an a priori fashion, then it follows that it cannot fail to be true, regardless of what happens in the world. Like "it is raining or it is not raining". — Agustino
I think you're conflating a priori with analyticity here. The principle of non-contradiction is the hallmark criteria, for Kant, of analyticity. a priori just means without experience. All analytic statements are a priori, but not all a priori statements are analytic (according to Kant).
Why? Why does the fact that physics "rests" (what does that even mean?) on it guarantee it certainty? — Agustino
Because mathematical knowledge and scientific knowledge are closely tied together. And isn't a guarantee just another way of expressing that we are certain?
Apodeictic certainty just means that a proposition must be true to the consciousness who holds it to be true.
So if we have one kind of geometry which predicts physical phenomena then we have a reason for holding that it must be true. It is universal and necessary.
In fact, if we have two kinds of geometry, and one geometry does a reasonably good job of predicting some phenomena, but the other geometry predicts all phenomena then we know which one is universal and necessary, and which one is merely necessary (and therefore empirical, i.e., not a priori).
It's not that math and physics are identical to one another, but it is our knowledge of math which guarantees the physics. If it turns out that our physics needs different maths then we were merely approximating in our first estimations the form of the intuition.
Can you explain how you can be wrong about your own subjectivity, and what you mean by that idea? — Agustino
What exactly are you after here?
I mean, it doesn't strike me as controversial at all. Especially at the level of abstraction that Kant is working at. To use your question later on -- why was Aristotle wrong about the categories? Why did it take so long for someone to formulate the critical philosophy and identify transcendental errors?
It's because we're stupid, on the whole. Humanity can perform feats of intellectual might which are very impressive. But, generally speaking, we aren't all that smart and we make mistakes and we believe false things all the time.
I doubt this. Kant does talk about apodeictic certainty innumerable times with regards to mathematics. Part of the TA project, as far as I see it, is to secure where the certainty of mathematics comes from - and for Kant, it comes from the (synthetic) a priority of its propositions. — Agustino
Yes he does but it doesn't mean the same thing, exactly, either. Mathematical propositions must be true -- therefore they are certain. There is no more to it than that.
What exactly is the relationship between the intuition and the understanding that causes us to be capable of forming wrong concepts based on the former? — Agustino
Why on earth would it not be possible to be wrong?
The relationship, as I see it, is one of flow. I see the understanding as flowing down and the intuition as flowing up. In the middle is the schemata, which connects the two different parts of the mind -- kind of like a baptism of the categories into the forms of intuition. The categories are distinct still, of course, it is only the schemata which is the union between the two.
It seems to me that we can be wrong about all manner of things, though. And in this case, with geometry, if the two geometries appear very similar within the world as we are presently living in it then there simply wouldn't be a reason to think there is another one. But then we lived in a different way and someone had some ideas and it turned out to be that we were wrong in some of our predictions.
Why exactly do you think we can't be wrong? Simply because the knowledge is universal and necessary?
In Kant's time, Euclidean geometry was both of those things. It wasn't until we developed different physics, different geometries, that Euclidean geometry -- as the mathematical model of physics (plus other maths, while we're at it) -- were seen to be approximations.
So, if space is transcendentally ideal, then there is no noumenal space, correct? — Agustino
Of the noumenal world nothing is known, period. So the proposition "The noumenal world is lacking space", while truth-apt, cannot be judged. There is no basis upon which such a judgment can rest. The noumenal world may have space, it may not. We simply do not know nor can we judge in either direction. To believe something along those lines would be to be doing metaphysics, which our understanding is incapable of turning into a science.
So why is it that it took so long for us to discover non-Euclidean geometry? — Agustino
Sort of a repeat question again, but why shouldn't it take us so long to discover non-Euclidean geometry?
It seems to me, paired with your balking about being wrong about subjectivity, that you're harboring some Cartesian sympathies for knowledge of the self.
That's fine and all, but if we're talking about Kantian philosophy then the self is not so central in his philosophy. Subjectivity is. But knowledge of the self is not given priority. It is not more certain. In fact, the most certain knowledge in Kantian philosophy is of mathematics and physics, and not psychology :D. (Kant didn't even think chemistry was a science proper.)
Also: certainty is definitely not as central in Kant's philosophy as it is in Descartes'.
According to this development of Kant, we gain knowledge by comparing our concepts with our intuition. Do you claim that, in our intuition, we knew that non-Euclidean geometry is possible? If we did, then why did it take so long for us to compare our concepts (Euclidean geometry) with our intuition, and find out that they were different?
I don't think the intuition knows anything. Knowledge is not generated without both parts of the mind. -
 Agustino
11.2kI will address the rest of the post soon, but first:
Agustino
11.2kI will address the rest of the post soon, but first:
Sure. Analytic statements are a priori because we don't need to appeal to experience to know that they are true. If geometric statements are also a priori, then we don't need to appeal to experience to know that they are true, correct? And if we don't need to appeal to experience to know that they are true, then experience cannot disconfirm them. But experience is able to disconfirm Euclid's 5th postulate. Thus it cannot be a priori, and yet we have mistaken it for a priori. How is it possible to know if the other geometric postulates we have aren't also mistaken to be a priori, when in truth, they really aren't? And if we can't know that they are a priori, then on what basis can we claim that space is a form of our intuition?I think you're conflating a priori with analyticity here. The principle of non-contradiction is the hallmark criteria, for Kant, of analyticity. a priori just means without experience. All analytic statements are a priori, but not all a priori statements are analytic (according to Kant). — Moliere -
 Agustino
11.2kTo build for a second on what I said above. To find out whether analytic statements are true, we appeal to the meanings / definitions of our words. To find out whether synthetic a posteriori statements are true, we appeal to experience. And to find out whether synthetic a priori statements are true, we appeal to the intuition (with regards to geometry at least). So we appeal to the intuition and find out that Euclid's 5th postulate is true. And yet, you claim that we were merely wrong about our intuition... but it doesn't make sense to be wrong about our intuition when it is our intuition to which we appeal to determine whether Euclid's 5th is true or not, isn't it?
Agustino
11.2kTo build for a second on what I said above. To find out whether analytic statements are true, we appeal to the meanings / definitions of our words. To find out whether synthetic a posteriori statements are true, we appeal to experience. And to find out whether synthetic a priori statements are true, we appeal to the intuition (with regards to geometry at least). So we appeal to the intuition and find out that Euclid's 5th postulate is true. And yet, you claim that we were merely wrong about our intuition... but it doesn't make sense to be wrong about our intuition when it is our intuition to which we appeal to determine whether Euclid's 5th is true or not, isn't it? -
 Moliere
6.5kGeometric statements are a priori synthetic. We appeal to the form of intuition, such as when we place dots on a sheet of paper, look at our fingers, or draw a triangle. There is no particular existent to which we appeal, this is true. But our intuition is involved, which is why it can be called knowledge in the first place -- it deals with cognition.
Moliere
6.5kGeometric statements are a priori synthetic. We appeal to the form of intuition, such as when we place dots on a sheet of paper, look at our fingers, or draw a triangle. There is no particular existent to which we appeal, this is true. But our intuition is involved, which is why it can be called knowledge in the first place -- it deals with cognition.
We determine if a proposition is a priori if it is universal and necessary. Universality applies across all space and time. Necessity is a category which modifies the copula in the logic. It is a modal category which deals with how we assent to some statement. Those three categories are problematic, assertoric, or necessary. Necessity does deal with certainty. But certainty is holding-to-be-true for everyone, i.e., objective. That's the meaning of certainty in Kant -- it's more about intersubjective agreement, and our attitude towards a proposition than anything else.
So, in Kant's time the propositions of Euclid were universal and necessary, hence a priori. Furthermore, the subject and the predicate of those axioms were synthetic in that the predicate was not contained within the subject.
Now, we may be able to still say they are universal and necessary, which is the idea I'm sort of toying with. But my original thought was that since we have non-Euclidean geometry which is universal, and now know that Euclidean geometry is not universal because of that, then Euclidean geometry would not have the sufficient conditions for being a priori -- it would still be necessary, but not universal. And we would know that because we have a geometry to compare it to which is universal.
The first approximated the second geometry.
Since they were so close we simply missed it. Plus, we developed other means of probing the shape of space which were not available in Kant's time -- without which we wouldn't have noticed the difference. -
 Agustino
11.2k
Agustino
11.2k
Thus it would be a priori according to Kant. It is sufficient for a proposition to be either necessary or universal to be a priori.it would still be necessary, but not universal. — Moliere
"Now, in the first place, if we have a proposition which contains the idea of necessity in its very conception, it is a if, moreover, it is not derived from any other proposition, unless from one equally involving the idea of necessity, it is absolutely priori [...] Necessity and strict universality, therefore, are infallible tests for distinguishing pure from empirical knowledge [...] But as in the use of these criteria the empirical limitation is sometimes more easily detected than the contingency of the judgement, or the unlimited universality which we attach to a judgement is often a more convincing proof than its necessity, it may be advisable to use the criteria separately, each being by itself infallible." -
 Agustino
11.2k
Agustino
11.2k
Although I disagree it would be necessary. Again - Euclid's 5th postulate contradicts non-Euclidean geometries by not allowing cases that non-Euclidean geometry does allow. Therefore, it cannot be necessary. So why was it that we thought it necessary in the first place? How is such a mistake at all possible (to use Kant's transcendental language :P )?it would still be necessary, — Moliere -
 Agustino
11.2k
Agustino
11.2k
Another one. Apparently, geometrical principles are united with the consciousness of their necessity - I don't see how that is the case with Euclid's 5th postulate. If we had the consciousness of its necessity, then we couldn't be wrong, could we? That consciousness cannot just vanish can it? So my prior question remains significant - how is it even possible to be mistaken about our a priori cognition as it relates to our pure intuition? This cognition is necessary, if it is necessary, then we cannot be mistaken about it - that seems to follow, necessarily, if I may say so.Geometry is a science which determines the properties of space synthetically, and yet a priori.
What, then, must be our representation of space, in order that such a cognition of it may be possible?
It must be originally intuition, for from a mere conception, no propositions can be deduced which go out beyond the conception, and yet this happens in geometry. But this intuition must be found in the mind a priori, that is, before any perception of objects, and consequently must be pure, not empirical,
intuition. For geometrical principles are always apodeictic, that is, united with the consciousness of their necessity, as: "Space has only three dimensions" — Kant -
 Agustino
11.2k
Agustino
11.2k
So then this is just about categorising statements, not about how things really are?Yes, true. I just mean how we categorize something, not what it is. — Moliere
The correct answer would be due to universality and/or necessity according to Kant I think.Well, it's a priori because it does not rely upon particular experience -- it is non-empirical. Space itself is classified as non-empirical. We don't come to know it through inference. Space, like time, is unique in this way: that it is both part of our intuition, and that it is non-empirical. — Moliere
I've asked this before, but for completeness sake, I'll ask it again to the above: how can we be wrong about judgements which are universal and necessary?What makes it knowledge is that we then compare our propositions generated in the understanding to the form of intuition. And since it is knowledge of the form of intuition it is also universal and necessary. — Moliere
If we are wrong, it seems to follow as the night follows day that they were not universal and necessary. And yet, lo and behold, we can be mistaken about statements being universal and necessary. But we determine that they are universal and necessary by appealing to our intuition. So then our intuition must be wrong. Or we must have appealed to something other than our intuition, when we thought we were appealing to our intuition.
Euclid's 5th postulate precludes forms of geometry that are actually possible in non-Euclidean geometry. Thus the two must be contradictory. If one is true, then the other cannot be true, except, maybe, in a limited situation.What is contradictory in them? Perhaps we are wrong in thinking that. — Moliere
If it must be true in the consciousness that holds it as true, and if it is true in virtue of appeal to the form of intuition, then it cannot ever cease to be true.Apodeictic certainty just means that a proposition must be true to the consciousness who holds it to be true. — Moliere
Ehmmm X-) - I don't think he was.To use your question later on -- why was Aristotle wrong about the categories? — Moliere
Here you forget that we cannot appeal to experience at all to justify a priori knowledge, and hence neither can we appeal to experience to disconfirm it.It seems to me that we can be wrong about all manner of things, though. And in this case, with geometry, if the two geometries appear very similar within the world as we are presently living in it then there simply wouldn't be a reason to think there is another one. But then we lived in a different way and someone had some ideas and it turned out to be that we were wrong in some of our predictions. — Moliere
Yes.Why exactly do you think we can't be wrong? Simply because the knowledge is universal and necessary? — Moliere
Agreed for the sake of this discussion. (I take the most coherent version of Kantianism to be the one outlined by Schopenhauer, so I actually disagree here).Of the noumenal world nothing is known, period. So the proposition "The noumenal world is lacking space", while truth-apt, cannot be judged. There is no basis upon which such a judgment can rest. The noumenal world may have space, it may not. We simply do not know nor can we judge in either direction. To believe something along those lines would be to be doing metaphysics, which our understanding is incapable of turning into a science. — Moliere
No, not really. I'm fully aware that we don't have knowledge of our own subjectivity in many regards (Freud's unconscious, etc.). However, I wanted you to explain how this works according to Kant.It seems to me, paired with your balking about being wrong about subjectivity, that you're harboring some Cartesian sympathies for knowledge of the self.
That's fine and all, but if we're talking about Kantian philosophy then the self is not so central in his philosophy. Subjectivity is. But knowledge of the self is not given priority. It is not more certain. In fact, the most certain knowledge in Kantian philosophy is of mathematics and physics, and not psychology :D. (Kant didn't even think chemistry was a science proper.) — Moliere -
 Thorongil
3.2kKant's notion of a noumenon, at any rate, is confused. He talks of the noumenon causing the phenomenon, which is nonsense, since causality is a category of the understanding, and hence can only apply to the phenomenon. — Agustino
Thorongil
3.2kKant's notion of a noumenon, at any rate, is confused. He talks of the noumenon causing the phenomenon, which is nonsense, since causality is a category of the understanding, and hence can only apply to the phenomenon. — Agustino
This is the standard and, I might add, Schopenhauerian criticism of Kant: that he claimed the noumenon causes the phenomenon. But this is an error so obvious and egregious that it offends the principle of charity greatly to assume a philosopher of Kant's caliber wasn't aware of it. I think he was and that the contradiction you impute of him here is only apparent. If causality is an a priori form of the understanding, then we cannot but conceive of the noumenon causing the phenomenon, even though such a relation may not obtain in reality.
Haven't looked at the rest of the thread, as it's beating a very dead horse. I've said my piece about space. -
 andrewk
2.1k
andrewk
2.1k
This sounds an interesting avenue to explore. As I recall our discussion of a few days ago, you are conscious of its necessity, and I am conscious of its non-necessity (importantly, that is not the same thing as being conscious of the necessity of its negation!).If we had the consciousness of its necessity, then we couldn't be wrong, could we? — Agustino
The way I see it, that either means that:
1. at least one of us is wrong about its necessity; or
2. its necessity is individual-dependent, so that we could both be correct and it is necessary for you but not for me.
I find the second one palatable but my secondary sources tell me that Kant was adamant that his a priori intuitions like the TA were not subjective. If that's correct then I think he'd roll in his grave at suggestion 2. -
 Janus
17.9kI'd caution against thinking of intuition as perception. Intuition is just one half of the mind which acts entirely differently from the other half of the mind -- the understanding.
Janus
17.9kI'd caution against thinking of intuition as perception. Intuition is just one half of the mind which acts entirely differently from the other half of the mind -- the understanding.
Or, another way of putting this would be to say there's the understanding and sensibility, and intuition is a part of sensibility. I'm not sure which way to put it, myself.
In either rendition though perception is a psychological phenomena -- it deals with how a particular mind, and how many similarly wired particular minds, come(s) to recognize some phenomena as that phenomena.
But in the case of Kant we're dealing more with how all particular minds arranged Kant-wise (just to be cheeky -- I forget the exact term Kant uses, but our minds are contrasted with an intellectual intuition to give an idea of what sorts of mind he means {EDIT: and, just in case, an intellectual intuition is something like the mind of god, where thinking something creates reality -- not trying to talk down, just trying to make sure I cover my bases}) come to have knowledge about the world -- and in particular synthetic a priori knowledge. It's not about how we see a particular phenomena as that phenomena, but rather how it is possible for us to know some subject is attached to a predicate synthetically and without having to rely upon particular experience.
Linguistically -- perception's "link" is the word "as", and knowledge's "link" is the copula. — Moliere
In my way of thinking there is perception, (animals also perceive) and then there is understanding; which includes various kinds of understandings: commonsense, practical, scientific, geometrical, mathematical, statistical, dialectical, and so on. This seems to be consonant with Kant's scheme if the following diagram from the SEP article you linked, which deals with Kant's views about space and time, is any indication.
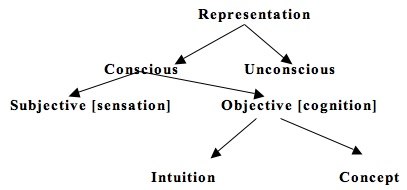
Of course. all these terms can be equivocal.
My original point was that space and time are the pure forms of intuition and are not themselves empirical, for Kant (and I think I remember reading you agreeing with this somewhere in this thread); whereas spacetime is an empirical model that predicts what will be observed. On that basis I can't see how, in the context of Kant's philosophy, the two can be thought to be the same. -
 Metaphysician Undercover
14.8kSo we appeal to the intuition and find out that Euclid's 5th postulate is true. And yet, you claim that we were merely wrong about our intuition... but it doesn't make sense to be wrong about our intuition when it is our intuition to which we appeal to determine whether Euclid's 5th is true or not, isn't it? — Agustino
Metaphysician Undercover
14.8kSo we appeal to the intuition and find out that Euclid's 5th postulate is true. And yet, you claim that we were merely wrong about our intuition... but it doesn't make sense to be wrong about our intuition when it is our intuition to which we appeal to determine whether Euclid's 5th is true or not, isn't it? — Agustino
Intuitions are inherently subjective. One intuition says Euclid's fifth is correct, another says it is not.
Again - Euclid's 5th postulate contradicts non-Euclidean geometries by not allowing cases that non-Euclidean geometry does allow. Therefore, it cannot be necessary. — Agustino
Take a long hard look at the way Kant uses "necessity". You know the principal use of "necessary" is the use which implies "needed for", and I think Kant's "necessity" is a derivative of this. So if in some geometries it is necessary for Euclid's 5th to be true, and in other geometries it is necessary that it is not true, there is no real contradiction, just like one logical possibility doesn't contradict the opposite possibility. The different geometries are simply based in different intuitions. -
 Moliere
6.5kMy original point was that space and time are the pure forms of intuition and are not themselves empirical, for Kant (and I think I remember reading you agreeing with this somewhere in this thread); whereas spacetime is an empirical model that predicts what will be observed. On that basis I can't see how, in the context of Kant's philosophy, the two can be thought to be the same. — Janus
Moliere
6.5kMy original point was that space and time are the pure forms of intuition and are not themselves empirical, for Kant (and I think I remember reading you agreeing with this somewhere in this thread); whereas spacetime is an empirical model that predicts what will be observed. On that basis I can't see how, in the context of Kant's philosophy, the two can be thought to be the same. — Janus
Yup, I agree with your reading of Kant. I hadn't thought of your argument though. I suppose I missed your point, originally, but I think I understand you now.
I think the tendency is to think of them in conflict because of the universal nature of space, and how we come to know about space through Euclidean geometry. That's what I was thinking, at least. It's universal and so either one or the other must apply.
But now I'm sort of wondering if Euclid, though it was one of Kant's primary examples of synthetic a priori knowledge, could be taken as just that -- an example. And perhaps both Euclidean space and non-Euclidean space could be thought to apply universally. That is, any geometry could count as knowledge, even universally, insofar that we are at least applying it to the form of intuition (so that it's not just analytic and true by definition, but true by virtue of a concept matching its object).
I'd be hesitant to say spacetime just doesn't apply. But I hear you when you are saying that because it is an empirical model it simply wouldn't be the space that Kant is talking about. That makes perfect sense to me.
What do you make of non-Euclidean geometry? Let's leave spacetime out of it entirely, and just focus on the mathematics. Do you think only one kind of geometry could hold universally for space? -
 Moliere
6.5kDoes it mean that it is a posteriori if we have to "probe the shape of space" for it? — Agustino
Moliere
6.5kDoes it mean that it is a posteriori if we have to "probe the shape of space" for it? — Agustino
No. Just as placing dots on a paper to demonstrate counting or addition, or drawing a triangle to demonstrate a triangle do not make mathematical knowledge a posteriori, so too with light. In terms of the intuition it is no different from using a ruler.
Although I disagree it would be necessary. Again - Euclid's 5th postulate contradicts non-Euclidean geometries by not allowing cases that non-Euclidean geometry does allow. — Agustino
So? How does that have anything to do with the modality of the copula, in Kant's logic?
Therefore, it cannot be necessary. So why was it that we thought it necessary in the first place? How is such a mistake at all possible (to use Kant's transcendental language :P )?
I think your use of "necessary" differs from Kant's use. Even in the introduction you quoted Kant downplays necessity stating that universality was the more impressive proof -- that necessity follows from universality. I agree that he links the two there, but if we're talking about "saving" the Kantian system then I don't think we'd have to hold that link. Though maybe so. It's been awhile since I've read the text, so I'm not sure.
Your saying "necessary" means not mistaken -- or, perhaps more strongly, not even possible to be mistaken. I am saying "necessary" means to give assent to by everyone, and hence be objective.
Another one. Apparently, geometrical principles are united with the consciousness of their necessity - I don't see how that is the case with Euclid's 5th postulate. If we had the consciousness of its necessity, then we couldn't be wrong, could we? — Agustino
Yes, we could.
That consciousness cannot just vanish can it?
Yes, it can.
So my prior question remains significant - how is it even possible to be mistaken about our a priori cognition as it relates to our pure intuition? This cognition is necessary, if it is necessary, then we cannot be mistaken about it - that seems to follow, necessarily, if I may say so.
This is why I think you're harboring some Cartesian sympathies here. It's like "necessary" and "certain" mean the same thing to you -- if some proposition is necessary then it is not possible for it to be false. But truth and falsity have nothing to do with necessity, in Kant'. Truth is when some concept matches its object. Necessity is about the quality some judgment has -- so we judge a proposition as necessary when it is objective, i.e., it holds for everyone.
I mean, of course these things can change in Kant's system -- especially considering that necessity, being a category, isn't even time-dependent. What happens in time can change when some proposition is necessary.
So then this is just about categorising statements, not about how things really are? — Agustino
That's what I was doing in that exchange, yes. I was categorizing statements.
I've asked this before, but for completeness sake, I'll ask it again to the above: how can we be wrong about judgements which are universal and necessary? — Agustino
They turn out to be false. It's something of a cheeky answer, but really I don't think it goes much more in depth than that. Some people claimed to square the triangle, in ages past. That was false too.
Euclid's 5th postulate precludes forms of geometry that are actually possible in non-Euclidean geometry. Thus the two must be contradictory. If one is true, then the other cannot be true, except, maybe, in a limited situation. — Agustino
Maybe we are dealing with a limited situation in this case. So both can be true, if not necessary and universal.
However, I wanted you to explain how this works according to Kant. — Agustino
He doesn't really go into psychology very much. But mathematics seems to form the heart of his philosophy of science. So it would just be the fact that it's not a science, that we can be wrong, and so forth. It's a mundane answer, but I don't think there is a deep answer. Kant's dealing with the structure of the mind, a structure we all share as compared to the contrast class of an intellectual intuition. It's not really about our subjectivity as much, though Kant uses the word "subjective" in his own way that fits within the philosophy.
The self and subjectivity and all of that just aren't really there to be talked about. And psychology and anthropology are only mentioned in passing. -
 Thorongil
3.2kWhere? — Moliere
Thorongil
3.2kWhere? — Moliere
In a multitude of PMs to Agustino and in the big thread he made a while back. My current thought is this, I suppose: there is no problem if non-Euclidean geometries are purely fictitious. I think they are, for they were "discovered" by fiddling with axioms, not from empirical observation. -
 Janus
17.9kWhat do you make of non-Euclidean geometry? Let's leave spacetime out of it entirely, and just focus on the mathematics. Do you think only one kind of geometry could hold universally for space? — Moliere
Janus
17.9kWhat do you make of non-Euclidean geometry? Let's leave spacetime out of it entirely, and just focus on the mathematics. Do you think only one kind of geometry could hold universally for space? — Moliere
I'm not a very sophisticated math person, but my understanding is that they evolved as investigations of what would obtain if you curved the usual two-dimensional plane of Euclidean geometry. It seems the results are intuitively obvious (graphically derived, I guess) in the context of hyperbolic, elliptical and spherical surfaces.
I guess non-Euclidean geometries are universally possible, just as the shapes that yield the various curves are possible shapes in three-dimensional space. I don't know, though; I'm not confident that that is not a pretty dumb thing to say, given my lack of expertise in the subject. -
 Thorongil
3.2kWhile I think space is a priori and that non-Euclidean geometry fails as an objection to its a priority, I might add, in line with my thoughts here, that I don't think much metaphysically rides on whether space is an a priori feature of the mind or an a posteriori physical entity of some kind. This isn't to say that endeavoring to determine the truth of the matter on this issue isn't interesting or important, but rather that it doesn't affect the basic idealism I hold to which distinguishes between reality and appearance as captured by Plato's Allegory of the Cave, or between the thing-in-itself and the phenomena, in Kantian jargon. This, to me, seems to remain quite untouched.
Thorongil
3.2kWhile I think space is a priori and that non-Euclidean geometry fails as an objection to its a priority, I might add, in line with my thoughts here, that I don't think much metaphysically rides on whether space is an a priori feature of the mind or an a posteriori physical entity of some kind. This isn't to say that endeavoring to determine the truth of the matter on this issue isn't interesting or important, but rather that it doesn't affect the basic idealism I hold to which distinguishes between reality and appearance as captured by Plato's Allegory of the Cave, or between the thing-in-itself and the phenomena, in Kantian jargon. This, to me, seems to remain quite untouched. -
 Agustino
11.2k
Agustino
11.2k
Not only Kant, but I also, find suggestion (2) to be ridiculous. Reality has to be a certain way, and it is the job of philosophy to investigate it. It would be contradictory if geometry was different for each different person, since then we would be unable to share a world and communicate at all.2. its necessity is individual-dependent, so that we could both be correct and it is necessary for you but not for me.
I find the second one palatable but my secondary sources tell me that Kant was adamant that his a priori intuitions like the TA were not subjective. If that's correct then I think he'd roll in his grave at suggestion 2. — andrewk -
 Agustino
11.2k
Agustino
11.2k
Ok.If causality is an a priori form of the understanding, then we cannot but conceive of the noumenon causing the phenomenon, even though such a relation may not obtain in reality. — Thorongil
I don't think so. At minimum, I think you should read my exchange with Moliere, starting from here:Haven't looked at the rest of the thread, as it's beating a very dead horse. I've said my piece about space. — Thorongil
https://thephilosophyforum.com/discussion/comment/152158
Non-Euclidean geometry strikes at the very possibility of the Transcendental Aesthetic. -
 andrewk
2.1k
andrewk
2.1k
That doesn't follow. The difference between a perfectly flat space and one that is curved very, very slightly would make no difference at all to the ability to communicate.It would be contradictory if geometry was different for each different person, since then we would be unable to share a world and communicate at all. — Agustino
Welcome to The Philosophy Forum!
Get involved in philosophical discussions about knowledge, truth, language, consciousness, science, politics, religion, logic and mathematics, art, history, and lots more. No ads, no clutter, and very little agreement — just fascinating conversations.
Categories
- Guest category
- Phil. Writing Challenge - June 2025
- The Lounge
- General Philosophy
- Metaphysics & Epistemology
- Philosophy of Mind
- Ethics
- Political Philosophy
- Philosophy of Art
- Logic & Philosophy of Mathematics
- Philosophy of Religion
- Philosophy of Science
- Philosophy of Language
- Interesting Stuff
- Politics and Current Affairs
- Humanities and Social Sciences
- Science and Technology
- Non-English Discussion
- German Discussion
- Spanish Discussion
- Learning Centre
- Resources
- Books and Papers
- Reading groups
- Questions
- Guest Speakers
- David Pearce
- Massimo Pigliucci
- Debates
- Debate Proposals
- Debate Discussion
- Feedback
- Article submissions
- About TPF
- Help
More Discussions
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum







