-
 fdrake
7.2kTherefore, she should retain her $10, as her prior for Joe having included $20 is sufficiently low. Regardless, before she inspects the second envelope, both outcomes ($5 or $20) remain possible. — Pierre-Normand
fdrake
7.2kTherefore, she should retain her $10, as her prior for Joe having included $20 is sufficiently low. Regardless, before she inspects the second envelope, both outcomes ($5 or $20) remain possible. — Pierre-Normand
You can conclude either strategy is optimal if you can vary the odds (Bayes or nonconstant probability) or the loss function (not expected value). Like if you don't care about amounts under 20 pounds, the optimal strategy is switching. Thus, I'm only really interested in the version where "all results are equally likely", since that seems essential to the ambiguity to me.
Your assertion that 'only two values are possible' for the contents of the envelopes in the two-envelope paradox deserves further exploration. If we consider that the potential amounts are $(5, 10, 20), we might postulate some prior probabilities as follows: — Pierre-Normand
As I wrote, the prior probabilities wouldn't be assigned to the numbers (5,10,20), they'd be assigned to the pairs (5,10) and (10,20). If your prior probability that the gameshow host would award someone a tiny amount like 5 is much lower than the gigantic amount 20, you'd switch if you observed 10. But if there's no difference in prior probabilities between (5,10) and (10,20), you gain nothing from seeing the event ("my envelope is 10"), because that's equivalent to the disjunctive event ( the pair is (5,10) or (10,20) ) and each constituent event is equally likely
Edit: then you've got to calculate the expectation of switching within the case (5,10) or (10,20). If you specify your envelope is 10 within case... that makes the other envelope nonrandom. If you specify it as 10 here and think that specification impacts which case you're in - (informing whether you're in (5,10) or (10,20), that's close to a category error. Specifically, that error tells you the other envelope could have been assigned 5 or 20, even though you're conditioning upon 10 within an already fixed sub-case; (5,10) or (10,20).
The conflation in the edit, I believe, is where the paradox arises from. Natural language phrasing doesn't distinguish between conditioning "at the start" (your conditioning influencing the assignment of the pair (5,10) or (10,20) - no influence) or "at the end" (your conditioning influencing which of (5,10) you have, or which of (10,20) you have, which is totally deterministic given you've determined the case you're in). -
 Pierre-Normand
2.9kYou can conclude either strategy is optimal if you can vary the odds (Bayes or nonconstant probability) or the loss function (not expected value). Like if you don't care about amounts under 20 pounds, the optimal strategy is switching. Thus, I'm only really interested in the version where "all results are equally likely", since that seems essential to the ambiguity to me. — fdrake
Pierre-Normand
2.9kYou can conclude either strategy is optimal if you can vary the odds (Bayes or nonconstant probability) or the loss function (not expected value). Like if you don't care about amounts under 20 pounds, the optimal strategy is switching. Thus, I'm only really interested in the version where "all results are equally likely", since that seems essential to the ambiguity to me. — fdrake
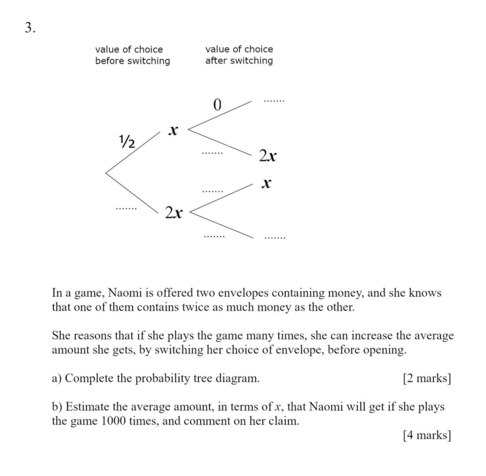
If we assume that all results are equally likely, the EV of switching given that the chosen envelope was seen to contain n is (2n + n/2)/2 - n = 1.5n. Hence whatever value n might be seen in the initially chosen envelope, it is irrational not to switch (assuming only our goal is to maximize EV). This gives rise to the paradox since if, after the initial dealing, the other envelope had been chosen and its content seen, switching would still be +EV.
As I wrote, the prior probabilities wouldn't be assigned to the numbers (5,10,20), they'd be assigned to the pairs (5,10) and (10,20). If your prior probability that the gameshow host would award someone a tiny amount like 5 is much lower than the gigantic amount 20, you'd switch if you observed 10. But if there's no difference in prior probabilities between (5,10) and (10,20), you gain nothing from seeing the event ("my envelope is 10"), because that's equivalent to the disjunctive event ( the pair is (5,10) or (10,20) ) and each constituent event is equally likely — fdrake
I did indeed first assigned priors to the two cases—(5, 10) and (10, 20)—and only derivatively calculated priors regarding the possible contents of the first chosen envelope (or of the other one).
Edit: then you've got to calculate the expectation of switching within the case (5,10) or (10,20). If you specify your envelope is 10 within case... that makes the other envelope nonrandom. If you specify it as 10 here and think that specification impacts which case you're in - (informing whether you're in (5,10) or (10,20), that's close to a category error. Specifically, that error tells you the other envelope could have been assigned 5 or 20, even though you're conditioning upon 10 within an already fixed sub-case; (5,10) or (10,20).
The conflation in the edit, I believe, is where the paradox arises from. Natural language phrasing doesn't distinguish between conditioning "at the start" (your conditioning influencing the assignment of the pair (5,10) or (10,20) - no influence) or "at the end" (your conditioning influencing which of (5,10) you have, or which of (10,20) you have, which is totally deterministic given you've determined the case you're in).
I am not conditioning within an already fixed sub-case. Seeing that there is $10 in one envelope still leaves it open that there might be $5 or $20 dollars in the other one. To be clear, you seems to be emphasizing the role of conditioning and timing, arguing that my observation of the $10 should not affect my decision about whether I'm in the (5,10) or (10,20) case. You appear to argue that, by the time I've observed the $10, the case is already determined, and I can't switch between cases based on my observation.
However, it seems that you've misunderstood my use of Bayesian updating. I am not arguing that observing the $10 allows me to switch between cases. Rather, I'm saying that, given an observation of $10, I can update my beliefs about the probability of being in the (5,10) case or the (10,20) case.
(Some further discussion with GPT-4)
RevealGPT-4
The only suggestion I would make is to add a sentence or two at the end summarizing your main point, to ensure it is clear to fdrake and others following the discussion. Something like:
"Essentially, I'm arguing that upon observing a value in the chosen envelope, we can revise our beliefs about the probabilities of the different cases, which subsequently alters the expected value of switching envelopes. This can resolve the two-envelope paradox without assuming a non-uniform prior or altering the objective of maximizing expected value."
Other than that, your reply seems to cover all necessary points.
PN:
I think what ultimately resolves the paradox is that when we don't actually observe the content of the initially chosen envelope, then the EV if switching is the weighted average of the EV of switching for all the suitably conditioned (updated) cases regarding the possible contents of the other envelope. And this EV is zero. Is that clear?
GPT-4
Yes, your point is clear.
When we don't observe the content of the initially chosen envelope, the Expected Value (EV) of switching indeed comes down to the weighted average of the EV for each possible content of the other envelope. This, however, requires an important assumption: the weights used in this average should represent our prior beliefs about the probabilities of each case (i.e., each possible content of the other envelope). The probabilities have to be updated (conditioned) based on the information available, which in this case is none as we don't observe the content of the initially chosen envelope.
If these conditions are met, and given that one envelope has exactly double (or half) the money of the other, the overall EV of switching is indeed zero, which aligns with our intuition that without any extra information, both envelopes are equally likely to contain the larger amount.
PN:
About your remark that "the probabilities have to be updated (conditioned) based on the information available, which in this case is none as we don't observe the content of the initially chosen envelope," what I am rather assuming is that, for whatever content n of the initially chosen envelope, the EV of switching in that particular case, conditionally on our being in that case, is equal to the EV of switching calculated by means of Bayesian updating if we were to gain knowledge that we are in that case. Hence, it is not being assumed that we actually have the information.
GPT-4
Ah, I see what you're getting at now. You're right. I apologize for misunderstanding your point.
In the case of the Two Envelopes Problem, you are considering the expected value of switching under each possible value of the initially chosen envelope (i.e., you're taking a "case by case" approach) and then averaging these values according to their prior probabilities. In other words, you are considering hypothetical situations in which you would know the value of the initially chosen envelope, even though you do not actually observe its content.
This approach effectively evaluates the average EV of switching without actually knowing the content of the initially chosen envelope, but considering all possible outcomes.
To rephrase and clarify: The expected value (EV) of switching needs to be calculated conditionally for each possible outcome. Then, these conditional EVs are averaged over, using the prior probabilities associated with each outcome (not necessarily uniform). As long as the expected values of switching are calculated properly, taking into account the specific conditions of each case, the overall expected value of switching will turn out to be zero, regardless of the specific shape of the prior distribution. This reflects the intuitive idea that without additional information, switching or not switching should yield the same overall expected outcome, hence resolving the paradox. -
 Srap Tasmaner
5.2kSince we've all been throwing code around, here's a curiosity in Prolog:
Srap Tasmaner
5.2kSince we've all been throwing code around, here's a curiosity in Prolog:
envelope_pair(X, [X,Y]) :- A is 2 * X, B is div(X, 2), ( maybe -> member(Y, [A,B]) ; member(Y, [B,A]) ). pick_envelope([A,B], X) :- ( maybe -> member(X, [A,B]) ; member(X, [B,A]) ).
Here's a swish link so you can try it out.
The idea is that if you run a query like this
envelope_pair(10, Pair), pick_envelope(Pair, Mine)
you'll be able to backtrack all the way up the tree and back down, like this:
?- envelope_pair(10,Pair), pick_envelope(Pair,Mine). Pair = [10, 20], Mine = 10 ; Pair = [10, 20], Mine = 20 ; Pair = [10, 5], Mine = 5 ; Pair = [10, 5], Mine = 10.
(There's a duplicate 10, but oh well. It shouldn't really be a tree but just a graph, since there's two routes from root to 10. Might redo it, but this was quick.)
This (nearly -- ignoring the dupe issue) represents @Michael's view of the problem construction.
BUT, the design of the actual problem is more like this:
?- envelope_pair(10,Pair), !, pick_envelope(Pair,Mine). Pair = [10, 5], Mine = 10 ; Pair = [10, 5], Mine = 5.
If you insert a cut between the two predicates, backtracking all the way up to the selection of the envelope pair is blocked. When you ask for more solutions, you get just the one, not three.
Another way of running it.?- envelope_pair(4,[A,B]), !, pick_envelope([A,B],Mine). A = 4, B = Mine, Mine = 8 ; A = Mine, Mine = 4, B = 8.
Asking for another solution -- backtracking -- corresponds cleanly to swapping. (It's why the predicates are written a little odd, to be both randomized and backtrackable.)
What does the cut correspond to? -
 Michael
16.6kIf we assume that all results are equally likely, the EV of switching given that the chosen envelope was seen to contain n is (2n + n/2)/2 - n = 1.5n. Hence whatever value n might be seen in the initially chosen envelope, it is irrational not to switch (assuming only our goal is to maximize EV). This gives rise to the paradox since if, after the initial dealing, the other envelope had been chosen and its content seen, switching would still be +EV. — Pierre-Normand
Michael
16.6kIf we assume that all results are equally likely, the EV of switching given that the chosen envelope was seen to contain n is (2n + n/2)/2 - n = 1.5n. Hence whatever value n might be seen in the initially chosen envelope, it is irrational not to switch (assuming only our goal is to maximize EV). This gives rise to the paradox since if, after the initial dealing, the other envelope had been chosen and its content seen, switching would still be +EV. — Pierre-Normand
I think I showed in the OP why this isn't the case. The EV calculation commits a fallacy, using the same variable to represent more than one value. That's the source of the paradox, not anything to do with probability. -
 fdrake
7.2kWhat does the cut correspond to? — Srap Tasmaner
fdrake
7.2kWhat does the cut correspond to? — Srap Tasmaner
Answering that gives you the origin of the paradox, right? -
 fdrake
7.2kHowever, it seems that you've misunderstood my use of Bayesian updating. I am not arguing that observing the $10 allows me to switch between cases. Rather, I'm saying that, given an observation of $10, I can update my beliefs about the probability of being in the (5,10) case or the (10,20) case. — Pierre-Normand
fdrake
7.2kHowever, it seems that you've misunderstood my use of Bayesian updating. I am not arguing that observing the $10 allows me to switch between cases. Rather, I'm saying that, given an observation of $10, I can update my beliefs about the probability of being in the (5,10) case or the (10,20) case. — Pierre-Normand
I think I see what you mean. Would you agree that which envelope pair you're in is conditionally independent of the observation that your envelope is 10? Assuming that equation (my envelope = 10) lets that "random variable which equals 10" remain random, anyway.
Seeing that there is $10 in one envelope still leaves it open that there might be $5 or $20 dollars in the other one. — Pierre-Normand
I think this depends how you've set up your random variables to model the problem. If you can assign a random variable to the other envelope and "flip its coin", so to speak, you end up in case C where there's a positive EV of switching.
I can see that you've assigned probabilities to the pairs (5,10) and (10,20), I'm still unclear on what random variables you've assigned probabilities to, though. Where are you imagining the randomness comes in your set up? -
 sime
1.2k
sime
1.2k
Since you're an R user, you might find it interesting to define a model in RStan, using different choices for the prior P(S) for the smallest amount S put into a envelope. Provided the chosen prior P(S) is proper, a sample from the posterior distribution P( S | X) , where X is the observed quantity of one of the envelopes, will not be uniform, resulting in consistent and intuitive conditional expectations for E [ Y | X] (where Y refers to the quantity in the other envelope) -
 Michael
16.6k
Michael
16.6k
I'm trying to understand your use of conditioning, so can we start at the very beginning?
Let be the amount in one envelope and be the amount in the other envelope.
I pick an envelope at random but don't look at the contents.
Let be the amount in my envelope.
Do you agree with this?
Next we look at the contents of our envelope and find it to contain £10.
We then want an answer to this:
My understanding is that given that we don't know the value of the other envelope, or how the values were initially chosen, is an uninformative posterior; it provides us with no new information with which to reassess the prior probability. As such, .
This seems to be where we disagree? -
 fdrake
7.2kAnother way of looking at it @Pierre-Normand. If you wanna update on what you see, it's gotta be the realisation of a random variable. I set it up like this:
fdrake
7.2kAnother way of looking at it @Pierre-Normand. If you wanna update on what you see, it's gotta be the realisation of a random variable. I set it up like this:
Initial Speciication
1. Someone flips a coin determining if the envelope pair is Heads=(5,10), Tails=(10,20)
2. They give you the resultant envelope pair.
3. You open your envelope and see 10.
3. doesn't tell you anything about the result of the coin flip in one. What's the expectation of "the other envelope"? That means assigning a random variable to it. How do you do that? I think that scenario plays out like this:
Two Flips Specifications
1. Someone flips a coin determining if the envelope pair is Heads_1=(5,10), Tails_1=(10,20). Call this random variable Flip_1.
2. They give you the resultant envelope pair.
3. You open your envelope and see 10.
4. You flip a coin, Heads_2 means you're in case (5,10) and the other envelope is 5. Tails_2 means you're in the case (10,20) and the other envelope is 20. Call this random variable Flip_2.
I'm abbreviating Heads to H, Tails to T and Flip to F.
The paradox is arising due to stipulated relationships between Flip_1 and Flip_2.
The following reflects the intuition that the coin flip in 1 totally determines the realisation of the envelope in 4. It equates the two random variables. Let's say that we can equate the random variable Flip_1 and Flip_2, that means they have the same expectation. The expectation of Flip_1 would be... how do you average a pair? You don't. The expectation of Flip_2 is transparently 12.5. That means you can't equate the random variables, since they have differing expectations. In essence, the first random variable chooses between apples, and the latter chooses between oranges.
Let's say that instead of there being an equation of Flip_1 with Flip_2, there's the relationship:
P( (H_1=H_2) = 1 )
P( (T_1 = T_2) = 1 )
But that would mean H_1=(5,10) is equal to H_2 = 5, and they aren't equal. Similarly with T_1 and T_2. So the relationship can't be that.
Then there's a conditional specification:
P(F_2 = H_2 | F_1=H_1)=1
P(F_2 = H_2 | F_1=T_1)=0
P(F_2 = T_2 | F_1=H_1)=0
P(F_2 = T_2 | F_1=T_1)=1
Which legitimately makes sense. Then we can ask the question: what does "You open your envelope and see 10" relate to? It can't be a result of F_1, since those are pairs. It can't be a result of F_2, since that's the other envelope. It seems I can't plug it in anywhere in that specification. It's been used in the definition of F_2, to "remove" 10 from the appropriate space of values and render that a coin flip.
In fact, "opening my envelope and seeing 10" and updating on that is only interpretable as another modification of the set up:
Bivariate Distribution Specification
1) You generate a deviate from the following distribution (S,R), where S is the other envelope's value and R is your envelope's value. The possible values for S are (5,10,20) and the possible value for R are the same. S and R have a bivariate distribution (S,R) with the constraint (S=2R or R=2S). It has the following probabilities defining it:
P(S=5, R=10) = 0.25
P(S=10, R=20) =0.25
P(S=20, R=10) = 0.25
P(S=10, R=5) =0.25
A Bayesian solution modifies this distribution. I've just assumed all envelope pairs are equally likely.
2) You then observe R=10.
3) That gives you a conditional distribution P(S=5)=0.5, P(S=20)=0.5
4) Its expectation is 12.5 as desired.
5) You should switch, as S|R=10 has higher expectation than 10.
A different loss function modifies step 4.
And with that set up, you switch. With that set up, if you don't open your envelope, you don't switch.
There's the question of whether the "Bivariate Distribution Specification" reflects the envelope problem. It doesn't reflect the one on Wiki. The reason being the one on the wiki generates the deviate (A,A/2) OR (A,2A) exclusively when allocating the envelope, which isn't reflected in the agent's state of uncertainty surrounding the "other envelope" being (A/2, 2A).
It only resembles the one on the Wiki if you introduce the following extra deviate, another "flip" coinciding to the subject's state of uncertainty when pondering "the other envelope":
1) You generate a deviate from the following distribution (S,R), where S is the other envelope's value and R is your envelope's value. The possible values for S are (5,10,20) and the possible value for R are the same. S and R have a bivariate distribution (S,R) with the constraint (S=2R or R=2S). It has the following probabilities defining it:
P(S=5, R=10) = 0.25
P(S=10, R=20) =0.25
P(S=20, R=10) = 0.25
P(S=10, R=5) =0.25
2) You get the envelope 10, meaning the other envelope is 5 or 20 with equal probability. Call the random variable associated with these values F_1.
3) That gives you a conditional distribution P(F_1=5)=0.5, P(F_1=20)=0.5
4) Its expectation is 12.5 as desired.
5) You should switch, as F_1 produces a gain of 2.5 over not switching.
In that model, there's no relationship between the bivariate distribution (S,R) and F_1. Trying to force one gets us back to the Two Flips Specification, and its resultant equivocations. The presentation above is not supposed to make sense as a calculation, it's supposed to highlight where the account would not make sense.
Since you're an R user, you might find it interesting to define a model in RStan, using different choices for the prior for the smallest amount S put into a envelope. Provided the chosen prior P(S) is proper, a sample from the posterior distribution P( S | X) , where X is the observed quantity of one of the envelopes, will not be uniform, resulting in consistent and intuitive conditional expectations for E [ Y | X] (where Y refers to the quantity in the other envelope) — sime
It would! -
 Michael
16.6kNot really, as we can only consider this from the perspective of the participant, who only knows that one envelope contains twice as much as the other and that he picked one at random. His assessment of and can only use that information.
Michael
16.6kNot really, as we can only consider this from the perspective of the participant, who only knows that one envelope contains twice as much as the other and that he picked one at random. His assessment of and can only use that information.
Is it correct that, given what he knows, ?
Is it correct that, given what he knows, ?
If so then, given what he knows, .
Perhaps this is clearer if we understand that means "a rational person's credence that his envelope contains the smaller amount given that he knows that his envelope contains £10". -
 Pierre-Normand
2.9kThere's the question of whether the "Bivariate Distribution Specification" reflects the envelope problem. It doesn't reflect the one on Wiki. The reason being the one on the wiki generates the deviate (A,A/2) OR (A,2A) exclusively when allocating the envelope, which isn't reflected in the agent's state of uncertainty surrounding the "other envelope" being (A/2, 2A).
Pierre-Normand
2.9kThere's the question of whether the "Bivariate Distribution Specification" reflects the envelope problem. It doesn't reflect the one on Wiki. The reason being the one on the wiki generates the deviate (A,A/2) OR (A,2A) exclusively when allocating the envelope, which isn't reflected in the agent's state of uncertainty surrounding the "other envelope" being (A/2, 2A).
It only resembles the one on the Wiki if you introduce the following extra deviate, another "flip" coinciding to the subject's state of uncertainty when pondering "the other envelope": — fdrake
In the Wikipedia article, the problem is set up thus: "Imagine you are given two identical envelopes, each containing money. One contains twice as much as the other. You may pick one envelope and keep the money it contains. Having chosen an envelope at will, but before inspecting it, you are given the chance to switch envelopes. Should you switch?"
Your setup for the bivariate distribution specification is a special case of the problem statement and is perfectly in line with it. Let's call our participant Sue. Sue could be informed of this specific distribution, and it would represent her prior credence regarding the contents of the initially chosen envelope. If she were then to condition the Expected Value (EV) of switching on the hypothetical situation where her initially chosen envelope contains $10, the EV for switching, in that particular case, would be positive. This doesn't require an additional coin flip. She either is in the (5, 10) case or the (10, 20) case, with equal prior (and equal posterior) probabilities in this scenario. However, this is just one hypothetical situation.
There are other scenarios to consider. For instance, if Sue initially picked an envelope containing $5, she stands to gain $5 with certainty by switching. Conversely, if she initially picked an envelope with $20, she stands to lose $10 with certainty by switching.
Taking into account all three possibilities regarding the contents of her initially chosen envelope, her EV for switching is the weighted sum of the updated (i.e. conditioned) EVs for each case, where the weights are the prior probabilities for the three potential contents of the initial envelope. Regardless of the initial bivariate distribution, this calculation invariably results in an overall EV of zero for switching.
This approach also underlines the flaw the popular argument that, if sound, would generate the paradox. If we consider an initial bivariate distribution where the potential contents of the larger envelope range from $2 to $(2^m) (with m being very large) and are evenly distributed, it appears that the Expected Value (EV) of switching, conditioned on the content of the envelope being n, is positive in all cases except for the special case where n=2^m. This would suggest switching is the optimal strategy. However, this strategy still yields an overall EV of zero because in the infrequent situations where a loss is guaranteed, the amount lost nullifies all the gains from the other scenarios. Generalizing the problem in the way I suggested illustrates that this holds true even with non-uniform and unbounded (though normalizable) bivariate distributions.
The normalizability of any suitably chosen prior distribution specification (which represents Sue's credence) is essentially a reflection of her belief that there isn't an infinite amount of money in the universe. The fallacy in the 'always switch' strategy is somewhat akin to the flaw in Martingale roulette strategies. -
 Srap Tasmaner
5.2kWhat does the cut correspond to?
Srap Tasmaner
5.2kWhat does the cut correspond to?
— Srap Tasmaner
Answering that gives you the origin of the paradox, right? — fdrake
In a sense yes. The cut is a "committed choice" thing, and you could take that as representing the dealer's not monkeying with the envelopes once he's offered them to you.
But we know how the game works objectively; the problem is why some ways of modeling your own epistemic situation as the player work and others, though quite natural, don't. It's clear that including the cut in your model works; but it's not as clear why you must include it.
It's not even perfectly clear to me what sort of epistemic move the cut is; what have I done when I've done that? I'm not considering certain options for backtracking; okay, but why shouldn't I consider those options? The dealer may not monkey with the envelopes after he presents them, but I still don't know which branch (perhaps of many) he went down, so why shouldn't I consider those?
It is, after all, simply true that the other envelope must contain half the value of mine or twice. (And the problem here doesn't seem to be spurious or-introduction, because {mine/2, mine*2} is the minimal set for which that claim is always true.)
But it's also just as clear that this not equivalent to the {x, 2x} framing. Both envelopes, mine included, are members of that set, but mine is of course never a member of {mine/2, mine*2}. Given a set that includes both, you get a proper disjunctive syllogism: whichever one I have, the other one can't be, so it's the only other one in the set. Reasoning from the "mine" framing isn't nearly so clean.
Feels like the explanation is right here, but I'm not quite seeing it. -
 fdrake
7.2kThis doesn't require an additional coin flip. She either is in the (5, 10) case or the (10, 20) case, with equal prior (and equal posterior) probabilities in this scenario. However, this is just one hypothetical situation. — Pierre-Normand
fdrake
7.2kThis doesn't require an additional coin flip. She either is in the (5, 10) case or the (10, 20) case, with equal prior (and equal posterior) probabilities in this scenario. However, this is just one hypothetical situation. — Pierre-Normand
I agree that it doesn't require an additional coin flip when you've interpreted it like you have. It's still a different interpretation than assigning a random deviate to the unobserved envelope after you've seen your envelope has 10 in it. The former is a distribution on pairs that you condition on the observation that your envelope is 10, then down to a univariate distribution. The latter takes the subject's epistemic state upon seeing their envelope and treats the unobserved envelope as a univariate coinflip. For the stated reasons, these aren't the same scenario as the random variables in them are different.
I do agree that if you fix (5,10) and (10,20) as the possible pairs, and you're in the bivariate case, it's rational to switch. The wikipedia article, instead, treats "A" as a random quantity, which is univariate. A prior on A is thus a prior on one variable. And it's not necessarily bounded - as you've pointed out previously, I believe.
In contrast, the priors in the bivariate case are all bounded - because they're on the probabilities of amounts being in envelopes. Probabilities get bounded priors since they lay in [0,1].
Why I'm drawing such a distinction between the Wikipedia case, and the one discussed in this thread, is because the Wikipedia case treats A as a random deviate, which already isn't a bivariate random variable. In that case, the remarks about unbounded support on A (the amount in the other envelope) make sense.
Taking into account all three possibilities regarding the contents of her initially chosen envelope, her EV for switching is the weighted sum of the updated (i.e. conditioned) EVs for each case, where the weights are the prior probabilities for the three potential contents of the initial envelope. Regardless of the initial bivariate distribution, this calculation invariably results in an overall EV of zero for switching. — Pierre-Normand
I agree in the bivariate set up. The (5,10) and (10,5) cases have opposite gains from switching, so do the (10,20) and (20,10) cases. They're all equally likely. So the expected gain of switching is 0. That's the expectation of switching on the joint, rather than conditional, distribution.
This approach also underlines the flaw the popular argument that, if sound, would generate the paradox. If we consider an initial bivariate distribution where the potential contents of the larger envelope range from $2 to $(2^m) (with m being very large) and are evenly distributed, it appears that the Expected Value (EV) of switching, conditioned on the content of the envelope being n, is positive in all cases except for the special case where n=2^m. — Pierre-Normand
This makes sense. If we're in the case on the wiki, where A is a random variable, A's set of possible values are in [0, inf). A "uniform" prior there gives you an infinite expectation (or put another way, no expectation). At that point you get kind of a "wu" answer, since expected loss doesn't make any sense with that "distribution".
If you assume both envelopes are unobserved in the Wiki case, and you want to force an expectation to exist, there's a few analyses you can do:
Give the support of a distribution on A an upper bound, [0,n], Making it a genuine uniform distribution. The expectation of A is n/2. The other envelope is stipulated to contain (2n) or (n/4) based on a coin flip. If this really reflects the unobserved envelope's sampling mechanism, the expectation of the other envelope is n(1+1/8), which gives you switching being optimal. Switching will always be optimal. What stops you from "reasoning the other way" in this scenario is that the order of operations is important, if my envelope has values (2n), (n/4) with expectation (1+1/8)n it can't be identical with the other envelope's random variable which has expectation (n/2). One is a coinflip, one is a guess about the value of A. This might be an engineer's proof, though. "Why can't you equate the scenarios?" "You know they have different expectations, because the order you assign deviates to the envelopes matters from the set up. "Your" envelope and "the other" envelope aren't symmetric".
Now consider the case where the values A and 2A are assigned to the envelopes prior to opening. This gives the pair (A, 2A) are the possibilities. The envelope is unopened. The agent gets allocated one of the two (A, or 2A) based on the result of a coinflip. If they know the possible amounts in their envelope are A and 2A, and they just don't know whether A is in their envelope and 2A is in the other, or vice versa, then the expectation of their envelope is 1.5A. So is the expectation of the other envelope. Switching is then of expected value 0.
The fallacy in the 'always switch' strategy is somewhat akin to the flaw in Martingale roulette strategies. — Pierre-Normand
I think that if the "always switch" strategy is wrong, it's only wrong when the sampling mechanism which proves it doesn't apply to the problem. It just isn't contestable that if you flip a coin, get 20 half the time and 5 half the time, the expectation is 12.5. The devil is in how this doesn't apply to the scenario.
In my view that comes down to misspecification of the sampling mechanism (like the infinite EV one), or losing track of how the random variables are defined. Like missing the asymmetry between your envelope and the other envelope's deviates, or equating the deviate of drawing a given pair (or the value A) with the subject's assignment of a deviate to the other envelope. -
 Mikie
7.2kHaving chosen an envelope at will, but before inspecting it, you are given the chance to switch envelopes. Should you switch?
Mikie
7.2kHaving chosen an envelope at will, but before inspecting it, you are given the chance to switch envelopes. Should you switch?
It’s like the Monty Hall problem. But in this case, there’s a 50/50 chance of choosing the envelope with the larger amount of money, so switching makes no sense. You’re not given any more information, so I really don’t follow the rest of the calculations.
[Edit — I see this has been gone over quite a bit, so forgive the late interjection.] -
 Michael
16.6kYou’re not given any more information, so I really don’t follow the rest of the calculations. — Mikie
Michael
16.6kYou’re not given any more information, so I really don’t follow the rest of the calculations. — Mikie
The argument is:
Let x be the amount in one envelope and 2x be the amount in the other envelope.
Let y be the amount in the chosen envelope and z be the amount in the unchosen envelope.
The expected value of z is:
Given that the expected value of the unchosen envelope is greater than the value of the chosen envelope, it is rational to switch. -
 Srap Tasmaner
5.2kThere are two reasonable ways to assign variables to the set from which you will select your envelope: {x, 2x} and {x, x/2}. Either works so long as you stick with it, but if you backtrack over your variable assignment, you have to completely switch to the other assignment scheme.
Srap Tasmaner
5.2kThere are two reasonable ways to assign variables to the set from which you will select your envelope: {x, 2x} and {x, x/2}. Either works so long as you stick with it, but if you backtrack over your variable assignment, you have to completely switch to the other assignment scheme.
Thus you can say, if I have the smaller, I have x and the other is 2x, or you can say, I have x/2 and the other is x. The main thing is that you have to use the same scheme for the other case, where you have the larger.
If you choose to label the envelope you've chosen "A", it's true that the other envelope contains either 2A or A/2, but that's because there are two consistent ways to assign actual variables, and the "or" there is capturing the alternative variable schemes available, not the values that might be in the other envelope. "A" is an alias for one of the members of {x, 2x} or for one of the members of {x, x/2}, but you still have to choose which before you can think about expected values.
The key is that "or" up there ("2A or A/2") is not a matter of probability at all; once you've chosen a set, which member of the chosen set A is, is a matter of probability. But we won't be summing over the possible choices of variable scheme. -
 Mikie
7.2kGiven that the expected value of the unchosen envelope is greater than the value of the chosen envelope, it is rational to switch. — Michael
Mikie
7.2kGiven that the expected value of the unchosen envelope is greater than the value of the chosen envelope, it is rational to switch. — Michael
Seems like nonsense to me. There’s a 50% chance of choosing the envelope with the greater money. That’s it. That’s all we’re given. If we were given any other information, as in the Monty Hall problem, then perhaps switching is correct. But in that problem you start with a 1/3 chance of choosing the prize, and another option is revealed afterwards. In this case, however, nothing has changed.
So what we’re left with is the claim that going through the motion of picking one envelope and then — with absolutely nothing else changing— switching and picking up the other envelope is somehow rational. That’s simply wrong.
Is it worth doing? Yes. But we have no way of improving our choice by switching, any more than switching our call of “heads” to “tails”.
The expected value doesn’t matter. That just tells you it’s profitable to take the bet, especially in the long run. It doesn’t change the probability of choice. If I offer $1,000,000 if it comes up heads and you pay me $100 if it comes up tails, that’s a very profitable bet to take — especially if run many times. But it tells us nothing whatsoever about whether to switch our call, because the probability of choosing correctly is still 50/50. The simple act of changing our minds doesn’t magically change that. -
 Srap Tasmaner
5.2kI see this has been gone over quite a bit — Mikie
Srap Tasmaner
5.2kI see this has been gone over quite a bit — Mikie
Going back five years.
The "puzzle" is not figuring out what the right way to analyze this is -- although @Michael did argue, at length, in the old thread, for switching, and there are some interesting practical aspects to switching in the real world where the probability distributions need to be possible -- but why a seemingly natural way to analyze the game is wrong. There's not even agreement among analysts about whether this is a probability problem. (I don't think it is.) -
 Michael
16.6kThere's not even agreement among analysts about whether this is a probability problem. (I don't think it is.) — Srap Tasmaner
Michael
16.6kThere's not even agreement among analysts about whether this is a probability problem. (I don't think it is.) — Srap Tasmaner
Neither do I. I believe I showed what the problem is in the OP. -
 Michael
16.6kSo what we’re left with is the claim that going through the motion of picking one envelope and then — with absolutely nothing else changing— switching and picking up the other envelope is somehow rational. That’s simply wrong. — Mikie
Michael
16.6kSo what we’re left with is the claim that going through the motion of picking one envelope and then — with absolutely nothing else changing— switching and picking up the other envelope is somehow rational. That’s simply wrong. — Mikie
Yes, the conclusion is certainly wrong. The puzzle is in figuring out which step in the reasoning that leads to it is false. -
 sime
1.2kHere's another analysis that only refers to credences , i.e subjective probabilities referring to the mental state of a believing agent - as opposed to physical probabilities referring to the physical tendencies of "mind-independent" reality.
sime
1.2kHere's another analysis that only refers to credences , i.e subjective probabilities referring to the mental state of a believing agent - as opposed to physical probabilities referring to the physical tendencies of "mind-independent" reality.
According to this interpretation of the paradox, the paradox is only psychological and concerns the mental state of an agent who derives contradictory credence assignments that conflict with his understanding of his mental state. So this interpretation isn't adequately analysed by appealing to a physical model.
Suppose the participant called Bob, before opening either envelope, tells himself that he knows absolutely nothing regarding the smallest quantity of dollars S that has been inserted into one of the two envelopes:
Before opening either envelope, Bob reasons that since he knows absolutely nothing about the value of S, that he should appeal to Laplace's principle of indifference (PoI) by assigning equal credence to any of the permissible values for S. He justifies this to himself by arguing that if he truly knows nothing about the value for S, then he doesn't even know the currency denominations that is used to describe S. So he assigns
P(S = s) = P(S = 2s) = P(S = 3s) = P(S = 4s) ..... for every positive number s.
There is only one "distribution" satisfying those constraints, namely the constant function P(S) = c ,
that cannot be normalised, where c is any positive number which can therefore be set to c = 1. This is called an 'improper prior', and it's use often results in conflicting credence estimates, as shown by other paradoxes, such as Bertrand's Paradox.
Having chosen this so-called "prior", Bob reasons that when conditioned on the unknown quantity S, the unknown quantity X in his unopened envelope has the value S with a subjective probability p, else the value 2S with subjective probability (1 - p):
P(X | S) = p Ind (X,S) + (1- p) Ind (X, 2S) (where Ind is the indicator function)
He again appeals to PoI and assigns p = 1/2 (which merely a non-informative proper prior)
Substituting his choices for P(S) and p, Bob realises that the unnormalised joint distribution P(S,X) describing his joint credences for S and X is
P (S , X) is proportional to 0. 5 Ind (X ,S) + 0.5 Ind (X , 2S)
Summing over S, he derives his credences for X, namely P(X) that he realises is also an improper prior.
P(X) is proportional to 1
Consequently, his subjective 'unnormalized' posterior distribution (which does in fact sum to 1, but is nevertheless the ratio of the two unnormalised distributions P(S,X) and P(X) ) is described by
P (S | X) 'is proportioanal to' 0. 5 Ind (X ,S) + 0.5 Ind (X , 2S)
Bob wonders what would happen if he were to naively compute expectations over this 'unnormalised' distribution. He decides to compute the implied expectation value for the unopened envelope V conditioned on the value of his unopened envelope:
P (V = 2x | X = x ) = P(S = x | X = x) = 0.5
P(V = 0.5 x | X = x) = 1 - P(S = x | X = x) = 0.5
E [V | X ] = 5/4 X
Bob decides that he cannot accept this expectation value, because it contradicts his earlier credences that are totally agnostic with regards to the states of S and X. However, Bob also knows that this conditional expectation value is a fallacious value, due to the fact that his subjective probability distribution P(S | X) isn't really normalised, in the sense of it being the ratio of two unnormalised distributions P(S,X) and P(X).
Bob therefore knows how to avoid the paradox, without needing to revise his earlier credences.
Crucially, Bob realises that his 'unnormalised' subjective distribution P(S | X) should only be used when calculating ratios of P(S | X) .
So instead of strongly concluding that E [ V | X ] = 5/4 X that involved averaging with respect to an unnormalised posterior distribution P(S | X), he reasons more weakly to only conclude
P(V= 2x | X = x) / P( V = 0.5x | X = x) = 1
Which merely states that his credences for V=2X and V=0.5X should be the same.
So if Bob is mad enough to reason with subjective probability distributions (which IMO should never be used in science, and which can be avoided even when discussing credences by using imprecise probabilities), Bob can nevertheless avoid self-contradiction without revising his earlier credences, simply by recognising the distinction between legitimate and non-legitimate expectation values. -
 fdrake
7.2kSo if Bob is mad enough to reason with subjective probability distributions (which IMO should never be used in science, and which can be avoided even when discussing credences by using imprecise probabilities — sime
fdrake
7.2kSo if Bob is mad enough to reason with subjective probability distributions (which IMO should never be used in science, and which can be avoided even when discussing credences by using imprecise probabilities — sime
As an aside, AFAIK Bayesian applied statistics uses priors not based on previously collected data all the time. I don't know if researchers care about the distinction between subjective and objective priors nowadays. -
 bongo fury
1.8k
bongo fury
1.8k -
 Michael
16.6k
Michael
16.6k
The in that case wasn't referring to the smaller value but to the value of the other envelope. I'll rephrase it to make it clearer:
Let be the amount in one envelope and be the amount in the other envelope.
Let be the amount in the chosen envelope and be the amount in the unchosen envelope.
Welcome to The Philosophy Forum!
Get involved in philosophical discussions about knowledge, truth, language, consciousness, science, politics, religion, logic and mathematics, art, history, and lots more. No ads, no clutter, and very little agreement — just fascinating conversations.
Categories
- Guest category
- Phil. Writing Challenge - June 2025
- The Lounge
- General Philosophy
- Metaphysics & Epistemology
- Philosophy of Mind
- Ethics
- Political Philosophy
- Philosophy of Art
- Logic & Philosophy of Mathematics
- Philosophy of Religion
- Philosophy of Science
- Philosophy of Language
- Interesting Stuff
- Politics and Current Affairs
- Humanities and Social Sciences
- Science and Technology
- Non-English Discussion
- German Discussion
- Spanish Discussion
- Learning Centre
- Resources
- Books and Papers
- Reading groups
- Questions
- Guest Speakers
- David Pearce
- Massimo Pigliucci
- Debates
- Debate Proposals
- Debate Discussion
- Feedback
- Article submissions
- About TPF
- Help
More Discussions
- Realities and the Discourse of the European Migrant Problem - A bigger Problem?
- Responses to Lozanski's article "The Gettier Problem No Longer a Problem"
- Turning the problem of evil on its head (The problem of good)
- Islamic sociological problem or merely a Quran problem?
- Problem of Evil poses problem for Theism
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum