-
 jorndoe
4.2kThe words "possible", "necessary" and "contingent" are modal terms.
jorndoe
4.2kThe words "possible", "necessary" and "contingent" are modal terms.
These are the definitions of possible and necessary, going by possible world semantics of modal logic:
- possibilities hold for (at least) one logically consistent world
- necessities hold for all logically consistent worlds
Here, a world is an all-inclusive entirety, that has no complement. (Easy to formalize with propositions, and the existential and universal quantifiers, enabling formal reasoning — see below if you care.)
Starting in the simple, what might be a possible world?
Maybe an unchanging world being 1 thing, that's self-identical, and that's it (illustrated by the "simple" world columns in the images below). Doesn't imply a contradiction. Doesn't have to be green for example. Anything necessary would then have to be the case for "simple" world, as well as all other consistent worlds; the necessary is unavoidable, as it were.
Some hold that 1+0=1 is necessary, i.e. is the case for all worlds (the additive identity).
Our world is obviously possible, whatever exactly it may be.

Here the columns are more religiously oriented suggestions of possible worlds:
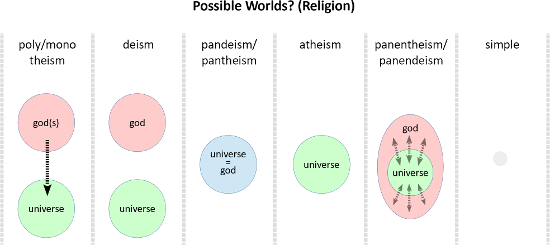
Where does that leave something defined as necessary, then? (Or if we suppose something exists that is necessary?) Platonism? What do all possible worlds have in common anyway? The "simple" world does not need green, life, sentience, or the likes, for example, to not derive a contradiction.
Reasoning about such sweeping universalities invariably falls back on a conjunction among "our world", and something like "simple" world, due to the fact that we're starting out with logic/mathematics in the first place (i.e. something akin to Platonism when ontologized/reified). However obvious self-identity (the 1st law) and 1+0=1 may be, they're not all that informative by themselves. Any necessities seem more like "inert" Platonic abstractions, should someone entertain such notions.
The negations of possible and necessary, respectively, are:
- not possible — does not hold for any consistent world — impossible
- not necessary — does not hold for all consistent worlds — either impossible or contingent
This is sometimes illustrated like so:
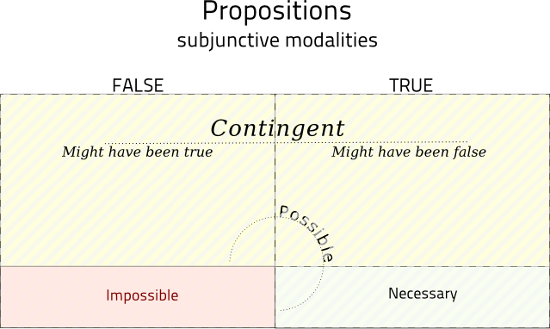
The formal definitions, at a glance, are as follows:
- possibly p ⇔ for some logical world w, p holds for w
- ◊p ⇔ ∃w∈W p
- necessarily p ⇔ for all logical worlds w, p holds for w
- □p ⇔ ∀w∈W p
- not possibly p ⇔ for no logical world w, p holds for w
- ¬◊p ⇔ ∀w∈W ¬p
- not necessarily p ⇔ for some logical world w, p does not hold for w
- ¬□p ⇔ ∃w∈W ¬p
Logical worlds, W, maintain standard logic:
- identity, x = x, p ⇔ p
- non-contradiction, ¬(p ∧ ¬p)
- the excluded middle, p ∨ ¬p
- double negation (introduction at least), p ⇒ ¬¬p
- modus ponens/tollens
In summary, necessities seem resigned to trivialities, perhaps like simple Platonic abstracts.
One might be inclined to ask if there even are any necessities...?
________
Image used for "our world" above © by Mark A Garlick
Additional credits to The Bare Necessities (1m:49s) from The Jungle Book (1967) by Disney -
 unenlightened
10kIn summary, necessities seem resigned to trivialities, perhaps like simple Platonic abstracts.
unenlightened
10kIn summary, necessities seem resigned to trivialities, perhaps like simple Platonic abstracts.
One might be inclined to ask if there even are any necessities...? — jorndoe
If a simple world is possible, not much is necessary.
In fact you have already made clear that all that is necessary for a possible world is that it obeys the standard rules of logic. This I would say is a constraint on how one can talk about it rather than what it is.
I conclude that anything is possible and nothing is necessary or impossible; necessity and impossibility reduce to the rules of talking sense, and talk does not constrain existence. -
 apokrisis
7.8kSurely worlds have logical properties that ordinary logic does not capture - because ordinary logic doesn't make general rules about spacetime and material action.
apokrisis
7.8kSurely worlds have logical properties that ordinary logic does not capture - because ordinary logic doesn't make general rules about spacetime and material action.
So the key constraints on actual worlds would seem to be the principle of locality and the principle of least action.
That is not everything can happen at once. All the action has to be spread out and take time. There is spacetime with its locality so that the world can logically exist via universalised differentiation.
And then in complementary fashion (where would metaphysics be without foundational dichotomies!), there must be also the logical rule that action follows its shortest possible paths. It spreads out and takes time, yet does so as little as possible. Hence the world is organised by a principle of universalised integration.
So even the simplest world is irreducibly complex in having to be this kind of unity of opposites. It must mathematically (let's call it Platonically) express the symmetry breaking that is differentiation~integration. Or in other words, it must be structured rationally as a self-organising fractal to exist ... because to exist, there must have been the possibility of a development, a symmetry breaking, and fractal maths describes symmetry breaking over all possible scales, or the development of maximal asymmetry.
Thus quite neatly, the world explains itself through some bare logical principles - the inescapability of the duo of differentiation and integration. You don't need extra stuff like creating gods messing up the picture. Disorganisation requires its own organisation to develop.
Welcome to The Philosophy Forum!
Get involved in philosophical discussions about knowledge, truth, language, consciousness, science, politics, religion, logic and mathematics, art, history, and lots more. No ads, no clutter, and very little agreement — just fascinating conversations.
Categories
- Guest category
- Phil. Writing Challenge - June 2025
- The Lounge
- General Philosophy
- Metaphysics & Epistemology
- Philosophy of Mind
- Ethics
- Political Philosophy
- Philosophy of Art
- Logic & Philosophy of Mathematics
- Philosophy of Religion
- Philosophy of Science
- Philosophy of Language
- Interesting Stuff
- Politics and Current Affairs
- Humanities and Social Sciences
- Science and Technology
- Non-English Discussion
- German Discussion
- Spanish Discussion
- Learning Centre
- Resources
- Books and Papers
- Reading groups
- Questions
- Guest Speakers
- David Pearce
- Massimo Pigliucci
- Debates
- Debate Proposals
- Debate Discussion
- Feedback
- Article submissions
- About TPF
- Help
- Other sites we like
- Social media
- Terms of Service
- Sign In
- Created with PlushForums
- © 2026 The Philosophy Forum





