Scientists don't need to think about philosophy all the time but they do this often while doing theoretical physics — Gregory

No argument from me.

Penrose's conformal cyclic cosmology says, according to his interviews, that the universe will expand until "it no longer knows what size it is". You have to think philosophically to unpack what that means — Gregory

And that is precisely what the Nobel Prize mathematician/physicist, Penrose, tosses at us. His is philosophical speculation by a revered scientist - not a non-scientist philosopher. That was my point. To philosophize in modern science one needs a science background.

The point being that philosophers can help scientists with conceptual orientation? — Banno

Yes, those poor scientists need a course in critical thinking skills taught by a philosopher. :roll:

Their ideas bring paradigm shifts which allow scientist to frame theoretical matters in new ways. Philosophers don't do the measurements but measurements can never stand alone without conceptualization of them and those concepts have much to do with what is discussed in philosophy — Gregory

You may have a point, but I am unconvinced. You would have to demonstrate this philosophical prowess in examples in the modern world, not olden times.

Namely, the decreasing amount of philosophers or scientists that exert too much of an effect on a field by making their name known.

Gödel did this to mathematics. — Shawn

He brought to light a fallibility in the subject, but it's not a concern in much of mathematics. However, in the future it may turn out to be very important. Who knows?

Weak emergence, weak relationships > The emergent properties apparently aren't very strongly connected to the parts — Kaiser Basileus

"Weak emergence" is a technical term and does not mean "weakly" emergent. It implies the equivalent of a computer program producing an unexpected and largely unpredictable outcome. Thus the image I posted.

. . . but science can't do without philosophy whether you like it or dislike it — Gregory

Progress in science requires lots of speculation by scientists, and some of this could be called philosophy. But to stipulate that philosophers untrained in science can trigger scientific revolutions is a stretch. :roll:

Emergence is identical to relationship — Kaiser Basileus

Here is one of my examples of weak emergence. What is the "relationship"?

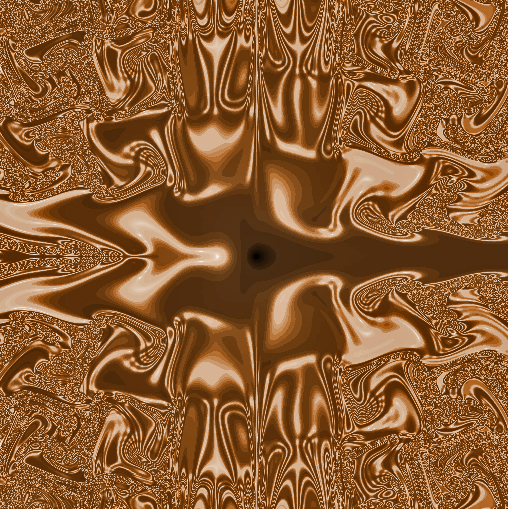
Human thought and ingenuity is paramount in creative mathematics. There is no way to determine this in advance. Lots of "aha!" moments. :cool:

So what are you on about jgill? And I mean that question literally; I have no idea what you're actually objecting to. Incidentally, no, calculus doesn't give us the GH paradox... broken intuitions do. I also find it a bit strange to claim that calculus is used to define the object; rather, it's used to analyze the object (surface area/volume in this case — InPitzotl

Math 631 (Algebraic Geometry) (U of Mich):

"Intended Level: Graduate students past the alpha algebra (593/594) courses. Students should either already know or be concurrently taking commutative algebra (Math 614). Students should also know the basic definitions of topology — we won't be using any deep theorems, but we will use topological language all the time. Basic familiarity with smooth manifolds will be very helpful, as much as what we do is the hard version of things that are done more easily in a first course on manifolds. Undergraduate students intending to take this course should speak to me about your background during the first week of classes."

This description speaks for itself. Correct me if I am mistaken, but it appears you have tossed in AG to impress the readers of this thread. If you are indeed a mathematics professor and feel AG is necessary, then I would understand. Are you? I was one for many years and we never had an undergraduate course in AG, although some schools do. GH always came up in a standard calculus course. Tell me where you are coming from and why you found it essential to define GH this way.

By the way, you should now go to the Wikipedia article on GH and inject your considered opinion. It's a nice piece and never mentions AG. You apparently think it should. Again, if you are or were a professional math person and have strong feelings about this I will understand.

From the link above: "So, I don't think anyone has addressed the question posed in the title; but, is complexity in mathematics in your opinion determinate?"

No. No more so than complexity in human thought is determinable.

What do you mean this has nothing to do with algebraic geometry? — InPitzotl

Whereas one can describe the collection of points in 3-space comprising GH with the zeros of
$P\left( x,y,z \right)={{z}^{2}}{{x}^{2}}+{{y}^{2}}{{x}^{2}}-1$, the paradox of GH does not emanate from that perspective, but from elementary calculus. Why even bring varieties up since it is irrelevant to the issue being discussed, and participants of the thread might well be familiar with the rudiments of calculus, but have little acquaintance with algebraic geometry?

A penny for your thoughts — TheMadFool

I'm glad to see you've left mathematics behind for the moment. :cool:

Gabriel's horn is an object defined using algebraic geometry. Algebraic geometry defines points in a space using coordinates using number lines. Number lines are defined with real numbers. — InPitzotl

Nonsense. This has nothing to do with algebraic geometry. G's Horn is elementary calculus. :roll:

You guys should just let this go and get back to epistemological metaphysics where accuracy is optional.

V = pi * (r approaching zero) * (r approaching zero) * (h approaching infinity) , (r approaching zero) * (h approaching infinity) = 1 — TheMadFool

Suppose r=1/n and h=n^2. Then V -> pi. You are not describing Gabriel's Horn.

If infinity = z then, — TheMadFool

This is mysterious. One should make pronouncements about topics familiar to one.

(Not being a philosopher, this makes me wonder if some of the "sophisticated" philosophical arguments on the forum are any better) :roll:

Possibilities in theoretical physics should be left to theoretical physicists, some of whom can be considered philosophers.

What kind of general syntax applies to proof telling? — Shawn

What is "proof telling"? Proof description? An actual proof written out? Compared with "story telling"?

A traditional proof (pencil on paper) may be complicated, but I take it "complexity" refers to computer programs that can ascertain correctness of proof for certain kinds of theorems.

I don't get your joke. We have two items in our list: apples and dollars, each of them forming a side of a right triangle. What's the hypotenuse in terms of apples and dollars? — TheMadFool

A number representing the square root of the square of the number of apples plus sixteen

What's the hypotenuse in terms of apples and dollars? That's all I'm asking. — TheMadFool

The square root of the square of the number of apples plus sixteen. An amazing breakthrough in marketing!

What is "congruent mathematics"? Just curious. — jgill

Geometry, mainly. — Shawn

The word "congruence" has at least two meanings in mathematics, but I've never come across a sub-discipline called "congruent mathematics".

Is every theorem able to provide for a proof that is least or more complex, and what this would itself amount to? I see that there's difficulty in understanding this because mathematicians aren't accustomed to treating logic as much as it used to to be about logicizing it. — Shawn

Do theorems "provide" for proofs? Especially ones that are "least complex" or "more complex"(than what?). And this is "logicizing" logic? :roll:

I'd like to see that! — SophistiCat


Thanks, maybe I'll get started on it. — fishfry

Yes indeed. Me too. :chin:

I do specifically think it applies to non-congruent mathematics — Shawn W

What is "congruent mathematics"? Just curious.

Just a thought: are there really that many proofs already available? Not at the library, certainly. — tim wood

Good point. I think of all the theorems I have conjectured and proven, each requiring intricate maneuverings, and wonder. During the past century generalizations and abstractions have been paramount, and certainly when an individual theorem lies within those domains its previously complicated proof may be subsumed by a general result. But this is probably not what the OP means.

One jumps to a higher order logic with supremums (least upper bounds) early in an undergraduate curriculum.

In as short as possible, would it be possible to entertain the notion that complexity in non-congruent mathematics is determinable? — Shawn W

? Maybe unscramble this. :chin:

Well done :up:

B-T is not easy for a non-mathematician, although the Wiki article does a good job. I encountered non-measurable sets over a half century ago, and happily left the subject behind. But, as happens when FF presents math material I clicked on it and was pleasantly surprised to find an actual fairly simple example on Wiki.

As r approaches 0, V too approaches 0 but, oddly, A doesn't — TheMadFool

Nonsense :roll:

I am no mathematician. — tim wood

I never liked math. — Outlander

Probably best, then, to avoid topics like this one.

Here's an example of a (weakly) emergent object called Infinite Brooch.



The intricate details are largely unpredictable from a process of composing a lengthy set of complex functions in the complex plane. Some think that the only true example of strong emergence is human consciousness. Another area of mathematics yielding emergent objects is cellular automata.

It seems inappropriate to consider reality as an emergent entity, for several reasons already mentioned. Weak emergence, on the other hand, can be fascinating.

This thread has become a little weird. But so are parts of physics. And math. :worry:

I'm not sure that knowing thyself is even possible, but what is more important is to know thy limitations. I was a rock climber for over half a century and learned that lesson early on.

Without physical things, how can significance be determined in statistics in a way that isn't arbitrary? — TiredThinker

The best hope of parapsychologists is to mathematically model ectoplasm, then run tests to see if the math is appropriate. But ectoplasm may have gone the way of aether. :worry:

Occasionally, in engineering and mathematics one discovers what seems to be a solution in search of a problem. I'm guilty of this. But this is mundane and not the philosophical nugget to which the OP refers. :cool:

But I don’t think this is about schadenfreude — Possibility

Agreed. Schadenfreude arises out of some aspect of envy. My daughter, a New Yorker, recently related to me a true case of SF: Some families who bought twenty million dollar entire floors in Manhattan high rises are complaining that their elevator doors are sluggish and there are dripping faucets that management is slow to fix. :cry:

. . . is the 1655 work by Hobbes that deals with mechanistic philosophy — Gregory

Wrong Hobbes. :roll:

although Hobbes wrote on physics. I don't know anything about his particular arguments — Gregory

He's my favorite philosopher!

Hobbes the philosopher

Consider each term of the form, 1/n , a momentary vibration. Count both directions , 1/n and -1/n . As you add up the moments the sums tend to plus and minus infinity and counting in both directions means counting backwards never ends. There is no "end of infinity". That's it for me. :meh:

Returning to the philosophical mundane, here is an appropriate passage on Nagel from Wikipedia:

Nagel is probably most widely known within the field of philosophy of mind as an advocate of the idea that consciousness and subjective experience cannot, at least with the contemporary understanding of physicalism, be satisfactorily explained using the current concepts of physics.

I agree. :smile:

Ye if we have an infinite series of vibrations (of fire!) stretching into the past with no end, then the future is different from the past because the past is completed infinity — Gregory

Wrong. Think of starting the harmonic series in both directions, then later popping into existence. At that point in time the series is still progressing negatively. But carry on.

Likewise, what's the probability of getting a number between 1 and 6, inclusive? Why, that would be 100% — TheMadFool

Not quite. There is an extremely small probability the die will end up balanced on an edge. Or that as you toss the die a meteor will crash into your home and blow everything to smithereens. Or any number of other weird things. A bit like Feynman with his path integral where he is tasked with computing a quantity for every possible path between points a and b.

But I didn't mean to interrupt the flow of your argument.

I'm very very interested in infinitesimals. Berkeley called them ghosts of dead space as if space dies as it approaches infinity. My question is why does it approach infinity when we get smaller and smaller but not when going in the opposite direction — Gregory

Have another glass of wine, my friend. :roll:

Here's a shape of time:

Lorentz Factor

There are schools here and there that teach calculus using infinitesimals, but by far most use the epsilon-delta approach.

https://matheducators.stackexchange.com/questions/5989/which-universities-teach-true-infinitesimal-calculus

↪jgill
Doesn't seem odd to me. If you want to do applied physics, do a physics degree. If you want to do theory, do maths. At my uni we had to take our electives in the maths department if we wanted to do advanced theoretical physics — Kenosha Kid

I've mentioned this before, but I was at the U of Chicago in the late 1950s and was surprised to learn that the physics department had entirely separated from the math department and required its students to take their math courses with them. This arrangement probably didn't last, but I just checked and saw that there might still be some minor friction between departments, with a comment that under a certain curriculum "you may have to learn . . . on your own".

I've had fun dabbling in simple vector fields in the complex plane, but quantum fields are quite a bit more complicated, even with a modest background in functional analysis. My hat's off to you guys. :cool: